网刊加载中。。。

使用Chrome浏览器效果最佳，继续浏览，你可能不会看到最佳的展示效果，

确定继续浏览么?

复制成功，请在其他浏览器进行阅读

云制造环境下的导向辊制造服务组合优化方法

- ORCID：
朱浪泽
- ORCID：
刘善慧
✉
- ORCID：
曹杨振
- ORCID：
杨红恩
- ORCID：
王远洋

西安理工大学印刷包装与数字媒体学院，陕西西安，710048

中图分类号： TS73

最近更新：2025-03-24

DOI：10.11980/j.issn.0254-508X.2025.03.019

目录contents

摘要

为改善云制造环境下导向辊的生产效率，本研究提出了一种基于改进NSGA-Ⅱ算法的导向辊制造服务组合优化方法。首先，分析导向辊组成及生产工艺，确定所需制造资源服务，从服务质量指标与柔性指标2方面，建立制造服务组合评价指标体系；其次，将双层规划思想引入制造服务组合优化领域，构建导向辊制造组合优化数学模型；最后，从种群初始化与遗传操作2方面，改进NSGA-Ⅱ算法，用以求解模型；通过2组实验，系统验证了所提方法相较于传统优化方法的性能优势。结果表明，本研究方法在种群多样性指标与收敛速度上均有较大提高，显著提升了导向辊制造服务组合优化问题的求解效率。

关键词

云制造; 导向辊; 组合优化; 造纸类机械; 改进NSGA-Ⅱ

导向辊是包装印刷与造纸类机械中最常见、用量最大的零件，其生产所需的制造资源具有海量性、多样性、异构性的特点^[

1]，在云制造环境下，导向辊的生产制造依赖云制造服务组合的形式^{[参考文献 2-3}2-3]。云制造服务组合是从加工能力不同的制造服务云池中选择合适的制造服务，将其组装成制造服务组合来执行制造任务^{[参考文献 4-5}4-5]。因此，实现导向辊制造服务组合的优选，是有效促进包装印刷与造纸类装备制造产业实现云制造的关键步骤之一。

制造服务组合优化的难点主要集中在组合优化模型构建和模型求解算法2方面。在组合优化模型构建方面，常用时间、成本、质量等服务质量（QoS）指标来评价服务组合效率^[

6-7]。除QoS指标之外，Yuan等^{[参考文献 8

百度学术}8]结合可组合性、可用性、可靠性构建云制造服务组合数学模型；Song等^{[参考文献 9

百度学术}9]提出了一种考虑服务不确定性的服务组合优化数学模型构建方法。近些年，在服务组合优化问题求解方面，元启发式算法成为了主流，常见类型包括多目标遗传（NSGA-Ⅱ）算法^{[参考文献 10

百度学术}10]、粒子群优化算法（PSO）^{[参考文献 11

百度学术}11]、人工蜂群算法^{[参考文献 12

百度学术}12]、蚁群算法^{[参考文献 13

百度学术}13]以及麻雀优化算法^{[参考文献 14

百度学术}14]等。Dutta等^{[参考文献 15

百度学术}15]使用NSGA-Ⅲ算法来寻找帕累托（Pareto）前沿；Zeng等^{[参考文献 16

百度学术}16]使用交叉优化算法（CSO）思想改进了教学优化算法（TLBO）的学习阶段，有效提高了大规模制造服务组合优化问题的求解效率。

综上所述，导向辊制造服务组合的优化方法目前还存在以下3个关键问题：①现有方法在解决一些存在用户需求偏好的服务组合优化问题时，不再适用；②现有求解算法在解决大规模服务组合问题时，效率较低且很难找到全局最优解；③在导向辊制造产业，利用现有云制造服务组合优化方法，无法得到最优的解决方案。

本研究提出了一种云制造环境下的导向辊制造服务组合优化方法，首先，分析导向辊结构及工艺流程，实现工序级任务分解，提出针对导向辊的云制造服务组合评价指标体系；其次，分别以云制造服务需求方和云制造平台运营方的利益作为双层规划模型的上下2层，构建导向辊制造组合优化数学模型；最后，基于改进的NSGA-Ⅱ算法完成模型求解。

1 云制造服务组合优化问题分析

云制造中的任务需求是连续且个性化的，首先，任务需求被提交到云平台，将被转化为制造任务，云平台将根据工艺流程将制造任务分解为多个子任务，每个子任务均对应1个能够完成该子任务的候选制造服务集；然后，从每个候选制造资源集合中选择1个制造资源形成制造服务组合；最后，根据所选择的优化目标，得到符合目标的最优制造服务组合。制造服务组合优化流程如图1所示。

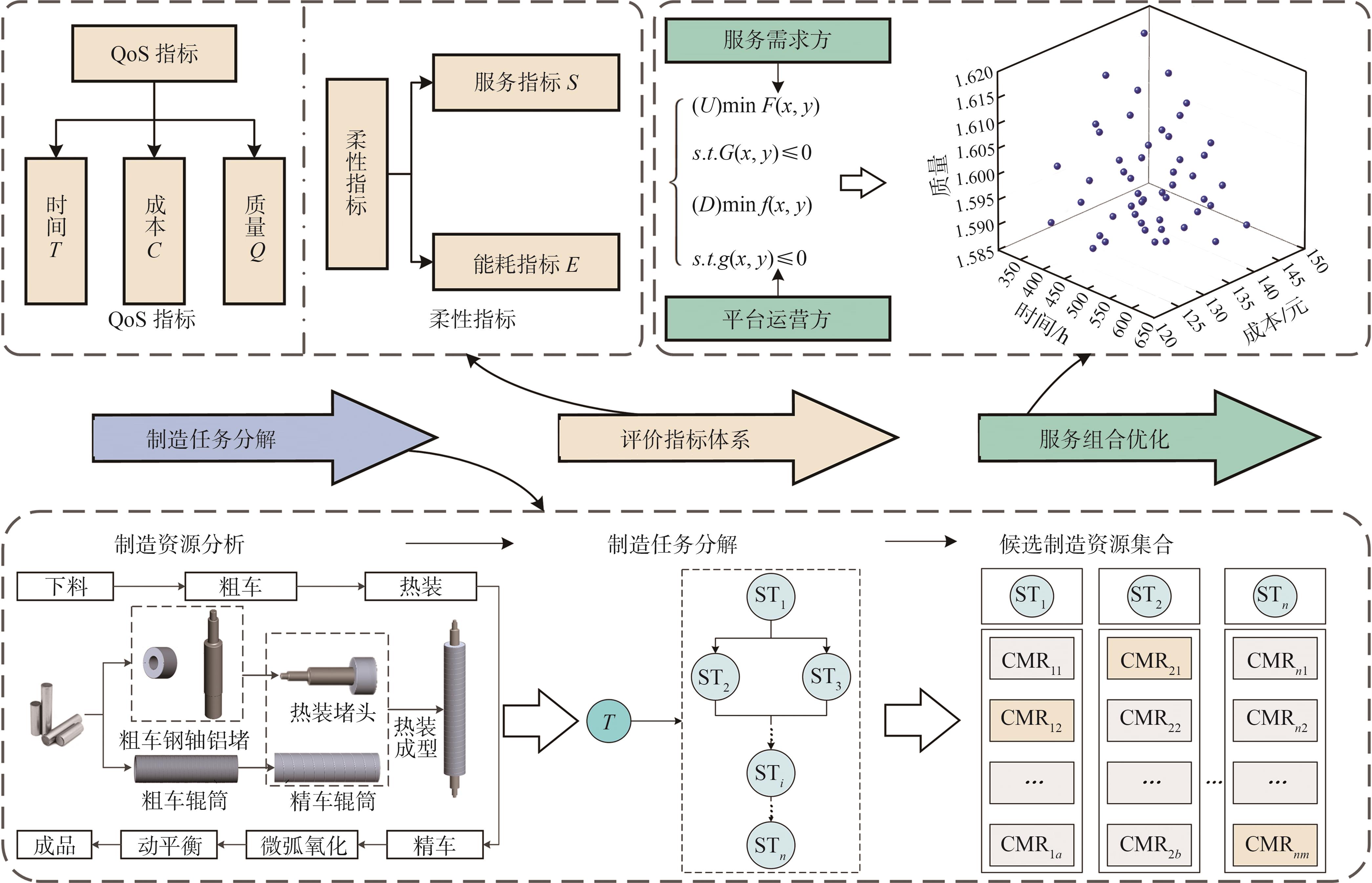
图1 制造服务组合与优化过程

Fig. 1 Process of manufacturing resource service composition optimization

由图1可知，制造服务组合优化流程可分为3部分，即制造资源分析与任务分解、构建组合优化评价指标体系和制造服务组合优化建模与求解。

1）制造资源分析与任务分解：当需求方用户向云制造平台提交制造需求时，该需求首先被转化为制造任务T。同时，在研究分析制造任务所需制造资源的基础上，将制造任务分解为n个子任务（即ST₁、ST₂、…、ST_i、…、ST_n）。对于每个子任务ST_i，存在可以满足需求的m_i个制造资源，因此，子任务ST_i对应的候选制造资源集合为CMR_i={CMR_i₁，CMR_i₂，…，CMR_imi}。

2）构建组合优化评价指标体系：组合优化评价指标体系的构建是实现组合优化模型构建的关键步骤，考虑服务需求方与平台运营方的利益，从QoS指标与柔性指标2方面构建组合优化评价指标体系。

3）制造服务组合优化建模与求解：将双层规划思想引入制造服务组合优化领域，以QoS指标和柔性指标分别作为上、下层的优化目标，构建导向辊制造服务组合优化数学模型。由于制造服务组合优化问题的求解是1个NP-Hard级的问题，因此需要用全局最优Pareto解才能满足需求。

2 云制造服务组合优化评价指标体系

在云制造环境下，构建服务组合优化评价指标体系是实现制造服务组合优化的前提和基础，因此本研究提出了针对导向辊的制造服务组合优化评价的指标体系。

2.1　导向辊制造任务分解

本研究围绕实际生产中最常见的钢轴导向辊展开，通过实际生产调研，得到导向辊的制造工艺流程及其所需制造资源，并根据所需加工设备的差异性，将导向辊制造任务分解为下料、车钢轴铝堵、车辊筒、热装、精车、微弧氧化、动平衡7道工序^[

17]。导向辊的基本结构和生产工艺流程如图2所示。

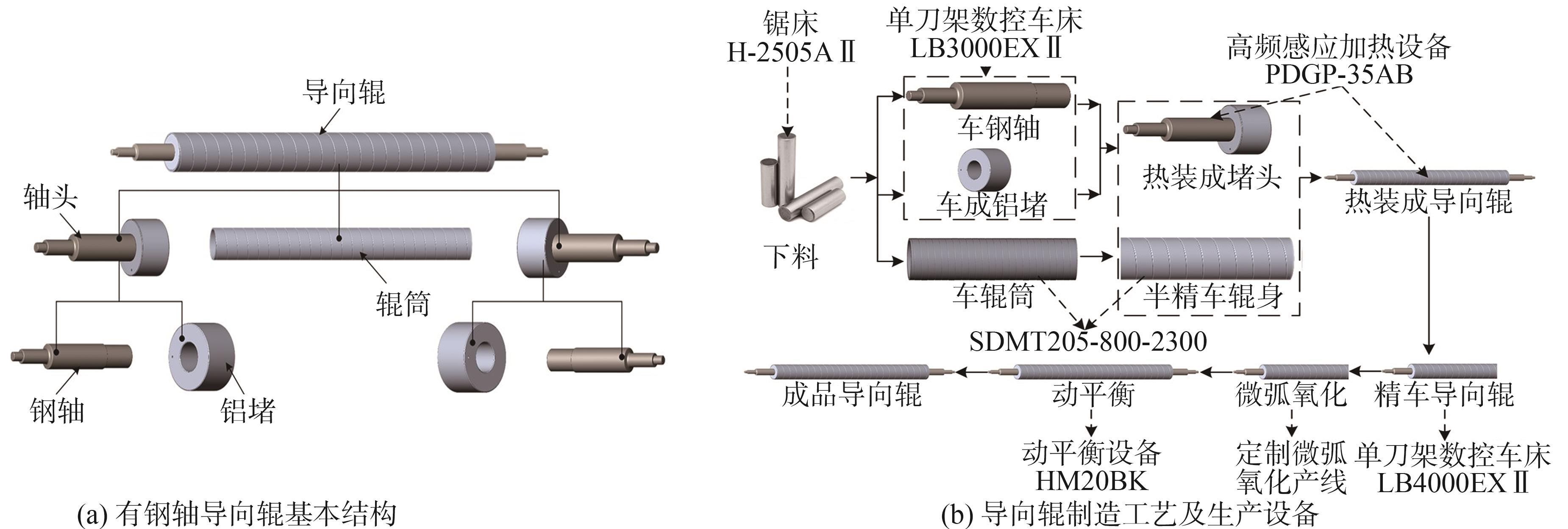
图2 导向辊结构及生产工艺流程

Fig. 2 Structure and production process of guide roller

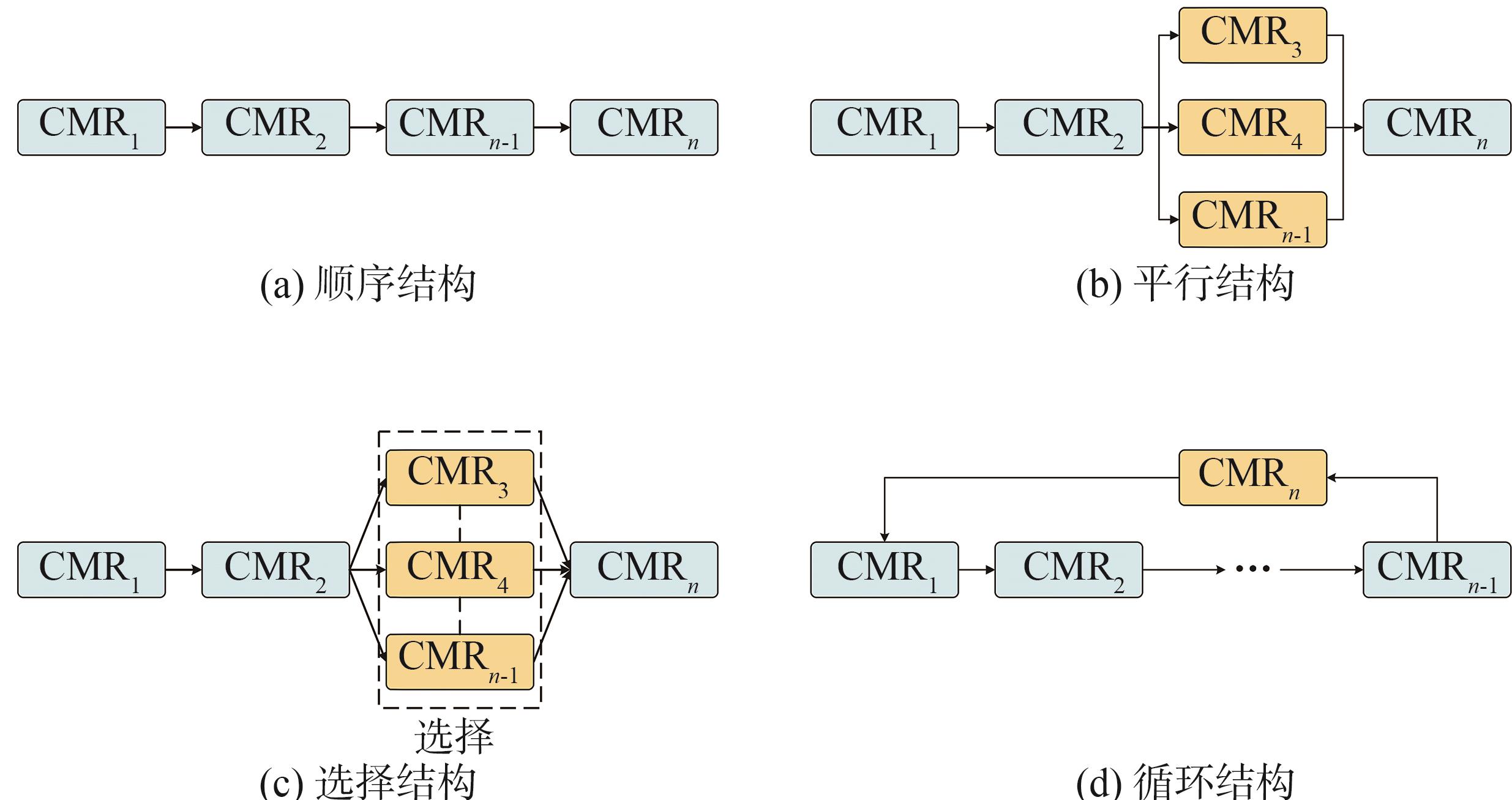
目前，在云制造环境下，制造服务组合可以描述为顺序、平行、选择和循环4种基本结构，如图3所示。由图3可知，顺序结构的特点是先完成前一个子任务，再开始后一个子任务，符合导向辊制造现状，因此，导向辊制造服务组合可以看作顺序结构。

图3 云制造服务组合4种基本结构

Fig. 3 Four basic structures of cloud manufacturing resource service composition

2.2　导向辊制造服务组合优化评价指标体系

为保障云制造服务顺利完成，需要综合考虑制造服务需求方、云平台运营方、制造服务提供方的利益以及服务过程中的不确定因素。因此，本研究提出考虑三方利益的导向辊云制造服务组合优化评价指标体系，指标类型及等级如表1所示。

表1 导向辊制造服务组合优化评价指标体系

Table 1 Evaluation index system of guide roller manufacturing service composition optimization

一级指标	指标类型	二级指标	三级指标
导向辊制造服务组合评价指标体系	QoS指标	时间T	加工时间T_p
			物流时间T_l
			交货时间T_d
		成本C	加工成本C_p
		成本C	物流成本C_l
		质量Q	质量合格率Q_s
	柔性指标	服务S	服务可用性S_r
			服务可靠性S_a
			服务成功率S_c
			服务评价S_e
		信誉R	交易信誉度R_t
		能耗指标E	节能设备水平E_e
		能耗指标E	节能制度水平E_s

导向辊云制造服务组合评价指标体系的QoS指标，包括时间T、成本C、质量Q。

1）时间指标T：包括加工时间T_p、物流时间T_l和交付时间T_d。

2）成本指标C：包括加工成本C_p和物流成本C_l。

3）质量指标Q：制造服务组合的质量指标用各个制造服务的平均质量合格率Q_s表示，即制造服务提供方完成相关任务的质量合格率。

除QoS指标之外，制造服务在完成过程中还会受到服务商状态的影响，因此，本研究提出了导向辊云制造服务组合优化柔性指标，包括导向辊制造服务提供商的服务能力S、信誉度R以及能耗指标E。

1）服务水平S：包括服务可用性S_r、服务可靠性S_a、服务成功率S_c和服务评价S_e。

2）信誉度R：以导向辊云制造服务商的交易信誉度R_t表示。

3）能耗指标E：包括制造服务提供方的节能设备水平E_e、节能制度水平E_s。

3 导向辊制造服务组合优化方法

3.1　导向辊云制造服务组合数学模型

双层规划（bilevel programming）模型是一种具有主从递阶结构的层次化模型^[

18]。上下层优化问题相对独立又相互依存，上层规划模型依靠下层优化问题的反馈来优化自身目标函数，下层规划模型在上层规划模型求解的基础上优化自身目标函数。双层规划模型的一般数学表达如式(1)所示。

\{\begin{array}{l} (U) m i n F (x, y) \\ s . t . G (x, y) \leq 0 \\ (D) m i n f (x, y) \\ s . t . g (x, y) \leq 0 \end{array}

（1）

式中，（U）和（L）分别为上层与下层规划；F、f分别为上、下层规划的目标函数；x、y分别为上、下层规划的决策变量；G、g分别是上、下层决策变量x和y的约束条件，且下层决策变量y是上层决策变量x的函数，即y=y(x)。

本研究以云制造服务需求方对QoS指标的优化目标作为上层决策主体，以云制造平台运营方对服务方的柔性指标的优化目标作为下层决策主体，建立如图4所示的导向辊制造服务组合优化数学模型。

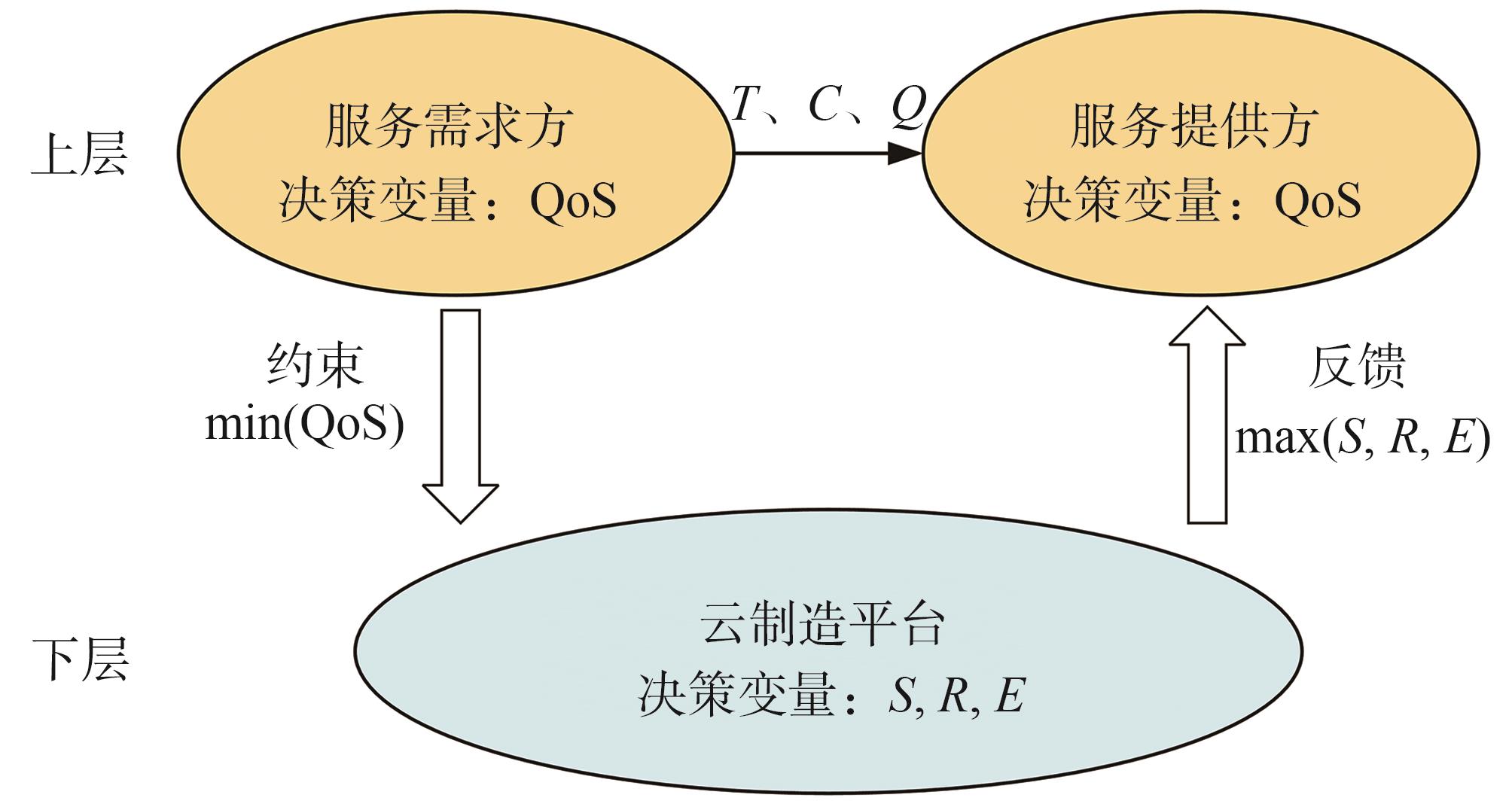
图4 导向辊制造服务组合优化问题数学模型

Fig. 4 Mathematical model for service composition optimization of guide roller manufacturing

3.1.1 上层规划模型

上层规划模型的优化目标包括总时间最小、总成本最低与质量最优，如式(2)所示。

\{\begin{array}{l} m i n T = \sum_{i = 1}^{n} T (i) = \sum_{i = 1}^{n} (T_{p} (i) + T_{l} (i) + T_{d} (i)) \\ m i n C = \sum_{i = 1}^{n} C (i) = \sum_{i = 1}^{n} (C_{p} (i) + C_{1} (i)) \\ m i n Q = Q_{s} = 1 - \sum_{i = 1}^{n} \frac{Q_{s} (i)}{n} \end{array}

（2）

3.1.2 下层规划模型

导向辊制造服务组合的下层柔性指标优化目标包括服务指标最优、信誉度最高以及能耗指标最高，如式(3)所示。

\{\begin{array}{l} m a x S = ω_{S_{r}} \sum_{i = 1}^{n} S_{r} (i) / n + ω_{S_{a}} \sum_{i = 1}^{n} S_{a} (i) / n + \\ ω_{S_{c}} \sum_{i = 1}^{n} S_{c} (i) / n + ω_{S_{e}} \sum_{i = 1}^{n} S_{e} (i) / n \\ m a x R = \sum_{i = 1}^{n} R_{t} (i) / n \\ m a x E = ω_{E_{e}} \sum_{i = 1}^{n} E_{e} (i) / n + ω_{E_{s}} \sum_{i = 1}^{n} E_{s} (i) / n \end{array}

（3）

分别确定上层规划和下层规划模型的优化目标之后，根据式(1)计算得到该导向辊制造服务组合优化双层规划模型，结果如式(4)所示。

\{\begin{array}{l} (U) m i n Q o S = ω_{t} (T / T_{m a x}) + ω_{c} (C / C_{m a x}) + \\ ω_{q} (Q / Q_{m a x}) \\ s . t . T \leq T_{m a x}, C \leq C_{m a x}, Q \geq Q_{m i n} \\ (L) m a x F = {(S, R, E)}^{T} \\ s . t . S_{r} (i) \geq S_{r m i n}, S_{a} (i) \geq S_{a m i n}, S_{c} (i) \geq S_{c m i n}, \\ S_{e} (i) \geq S_{e m i n} \\ R_{t} (i) \geq {R_{t}}_{m i n} \\ E_{e} (i) \geq E_{e m i n}, E_{s} (i) \geq E_{s m i n} \end{array}

（4）

式中，ω_t、ω_c和ω_q分别表示时间、成本和质量的权重系数；T_max、C_max和Q_max分别代表制造资源需求方对于时间、成本和服务质量的约束条件，其中，Q_max=1-Q_min；S_rmin、S_amin、S_cmin和S_emin分别表示平台运营方对服务指标的约束；R_tmin表示最低信誉度；E_emin和E_smin分别表示节能设备水平和节能制度水平的最低约束。

3.2　基于NSGA-Ⅱ的模型求解方法

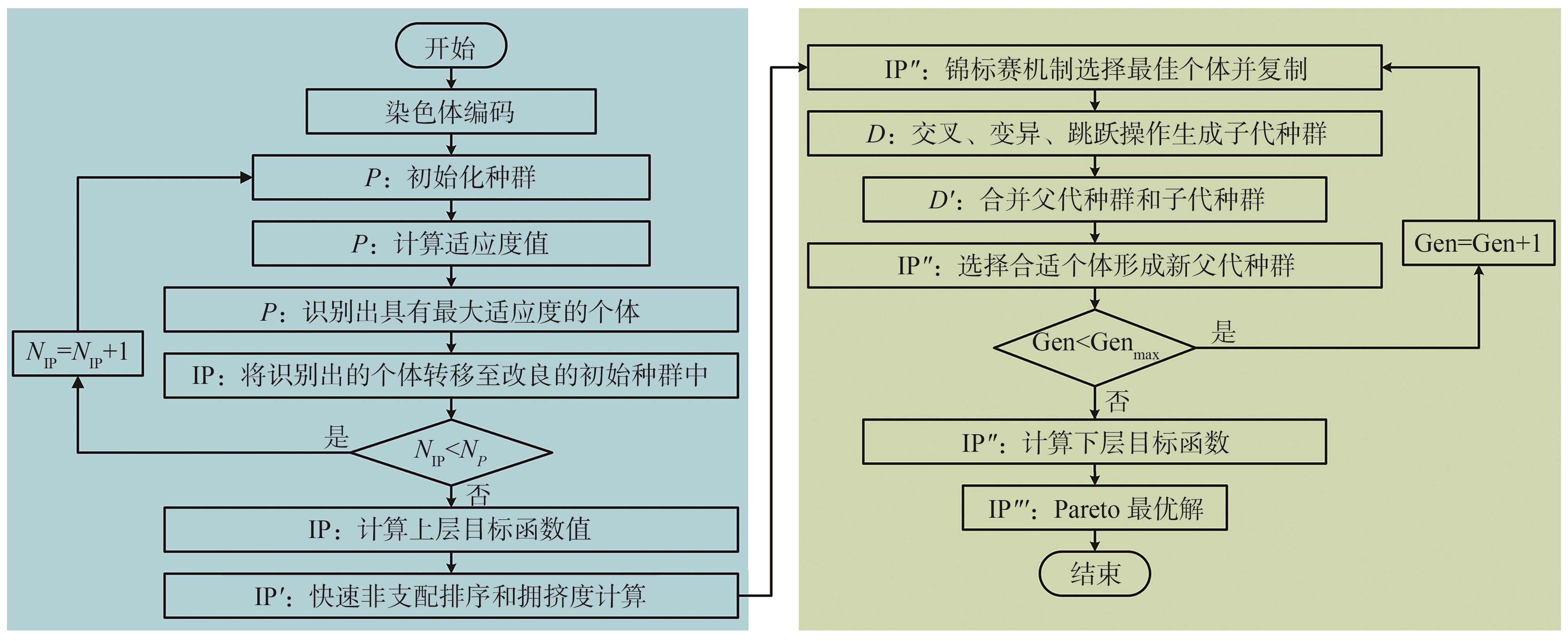
传统NSGA-Ⅱ算法具有复杂度低、整体进化水平高等优点，已被广泛地应用于云制造资源优化配置领域，但仍存在易陷入局部最优、收敛速度慢等问题。因此，本研究从遗传操作与初始种群筛选2方面对NSGA-Ⅱ算法进行改进。一方面，在遗传操作环节加入了跳跃因子，有效改善NSGA-Ⅱ算法的种群多样性，降低算法求解陷入局部最优的可能性；另一方面，在种群初始化阶段加入最佳适应度筛选机制，得到更优的初始种群，从而提高全局最优解的收敛速度。使用改进的NSGA-Ⅱ算法求解导向辊制造服务组合双层规划模型的步骤如图5所示。由图5可知，改进NSGA-Ⅱ算法求解导向辊制造服务组合双层规划模型的步骤共计12步，具体如下。

图5 改进NSGA-Ⅱ算法流程

Fig. 5 Flowchart of the improved NSGA-Ⅱ algorithm

1）步骤1：制造服务组合染色体编码，在NSGA-Ⅱ算法中，每个制造服务组合对应1个个体，采用整数编码的方法完成制造服务组合染色体编码。以服务组合CMR₁₁-CMR₂₂-CMR₃₂-CMR₄₃-CMR₅₂-CMR₆₄-CMR₇₁为例，其染色体编码为1-2-2-3-2-4-1。

2）步骤2：随机生成种群数量为N的初始种群P。

3）步骤3：根据式(2)计算初始种群P中各个个体的上层优化目标适应度值。

4）步骤4：根据步骤3中计算得到的个体适应度值，找出具有最大适应度值的个体，并将其转移至改良的初始种群IP。

5）步骤5：判断改良的初始种群IP的种群大小。若N_IP<N_P，则重新执行步骤2，循环次数加1；若N_IP＝N_P，循环结束，继续执行下一步骤。

6）步骤6：对初始种群筛选出的改良初始种群IP中的个体，进行非支配等级及拥挤度排序。

7）步骤7：根据步骤6得到的个体非支配等级和拥挤度排序，采用二元锦标赛机制，选择改良初始种群中更优的个体，形成父代种群IP"。

8）步骤8：对父代种群IP"进行交叉、变异、跳跃操作，形成子代种群D。交叉、变异是遗传算法最常见的2种遗传算子，跳跃算子主要包括剪切粘贴和复制粘贴2种类型，剪切粘贴是将染色体某段基因进行剪切并粘贴至新位置，复制粘贴是将某段基因复制后覆盖另一位置的基因。

9）步骤9：将父代种群与子代种群合并成种群规模为2N的新种群IPD。

10）步骤10：采用精英保留策略从新种群IPD中选择更优的N个个体，形成新的父代种群IP"'。

11）步骤11：收敛条件判断，若迭代次数Gen<设定的最大迭代次数Gen_max，则继续遗传迭代；迭代次数Gen加1；若迭代次数Gen=设定的最大迭代次数Gen_max，则迭代结束，执行步骤12。

12）步骤12：计算下层目标函数值，输出最优Pareto解集。

3.3　多目标算法评价指标

选择世代距离（generational distance，GD）与反转世代距离（inverted generational distance，IGD）2种指标来评估算法性能，具体如下所示。

1）GD是用来衡量算法求得解集的收敛状态的指标^[

19]，其计算如式(5)所示。GD数值越小，表明算法的解集收敛性能越好，其获得的非支配解更加逼近真实Pareto前沿上的所有解。

G D (P, P^{*}) = \frac{\sqrt[]{\sum_{y \in P} m i n_{x \in P^{*}} {(d (x, y))}^{2}}}{|P|}

（5）

式中，P表示由算法求解得到的Pareto边界的近似集；P^*表示决策空间中解均匀分布于最优Pareto边界上；d(x，y)表示2个决策向量x和y之间的欧几里得距离；P表示获得的Pareto前沿上解的总数。

2）IGD能够反映算法的综合性能，其计算如式(6)所示。IGD数值越低，表明获得的非支配解更加逼近真实Pareto前沿上所有解，最终收敛和多样性更好，即算法综合性能越理想^[

20]。

I G D (P, P^{*}) = \frac{\sqrt[]{\sum_{x \in P^{*}} m i n_{y \in P} {(d (x, y))}^{2}}}{|P^{*}|}

（6）

4 实验验证

为验证所提出的模型、方法的可行性和优越性，本研究分别设计了算法性能测试和实例验证。使用Matlab语言，在Matlab R2022a软件上完成实验验证，操作系统版本为Windows11 22H2，内存为16 GB。

4.1　算法性能分析

选择ZDT系列函数作为基准测试函数，分别为ZDT1~ZDT4，引入NSGA-Ⅱ算法、PSO算法作为对比算法，在相同实验环境下，设置种群规模50，交叉概率0.95，变异概率0.05，跳跃概率0.5，最大迭代次数200。PSO算法中设置ω_max和ω_min分别为1.2和0.3，学习因子均设置为1.5，每组实验进行20次。根据式(5)和式(6)计算GD与IGD值，结果如表2所示，算法性能对比情况如图6所示。

表2 GD与IGD测试结果

Table 2 Test results of GD and IGD

均值（标准差）	GD	IGD
ZDT1	8.46×10^-5 (1.07×10^-9)	2.38×10^-4 (5.97×10^-8)	8.39×10^-5 (2.21×10^-8)	5.64×10^-4 (6.88×10^-9)	7.98×10^-4 (1.01×10^-8)	5.51×10^-4 (7.05×10^-9)
ZDT2	7.54×10^-5 (2.67×10^-10)	8.98×10^-5 (3.32×10^-10)	7.96×10^-5 (3.97×10^-10)	1.49×10^-3 (2.50×10^-8)	3.20×10^-3 (1.40×10^-7)	1.60×10^-3 (2.45×10^-8)
ZDT3	2.59×10^-4 (1.27×10^-9)	4.24×10^-4 (8.76×10^-9)	2.82×10^-4 (4.21×10^-9)	3.21×10^-3 (6.07×10^-8)	5.44×10^-3 (1.75×10^-6)	3.32×10^-3 (8.59×10^-8)
ZDT4	5.09×10^-3 (1.75×10^-7)	8.56×10^-3 (3.46×10^-6)	5.20×10^-3 (2.71×10^-7)	1.59×10^-3 (2.46×10^-9)	2.08×10^-3 (5.24×10^-8)	1.69×10^-3 (5.60×10^-9)

均值

（标准差）

IGD

改进NSGA-Ⅱ

NSGA-Ⅱ

PSO

改进NSGA-Ⅱ

NSGA-Ⅱ

PSO

ZDT1

8.46×10^-5

(1.07×10^-9)

2.38×10^-4

(5.97×10^-8)

8.39×10^-5

(2.21×10^-8)

5.64×10^-4

(6.88×10^-9)

7.98×10^-4

(1.01×10^-8)

5.51×10^-4

(7.05×10^-9)

ZDT2

7.54×10^-5

(2.67×10^-10)

8.98×10^-5

(3.32×10^-10)

7.96×10^-5

(3.97×10^-10)

1.49×10^-3

(2.50×10^-8)

3.20×10^-3

(1.40×10^-7)

1.60×10^-3

(2.45×10^-8)

ZDT3

2.59×10^-4

(1.27×10^-9)

4.24×10^-4

(8.76×10^-9)

2.82×10^-4

(4.21×10^-9)

3.21×10^-3

(6.07×10^-8)

5.44×10^-3

(1.75×10^-6)

3.32×10^-3

(8.59×10^-8)

ZDT4

5.09×10^-3

(1.75×10^-7)

8.56×10^-3

(3.46×10^-6)

5.20×10^-3

(2.71×10^-7)

1.59×10^-3

(2.46×10^-9)

2.08×10^-3

(5.24×10^-8)

1.69×10^-3

(5.60×10^-9)

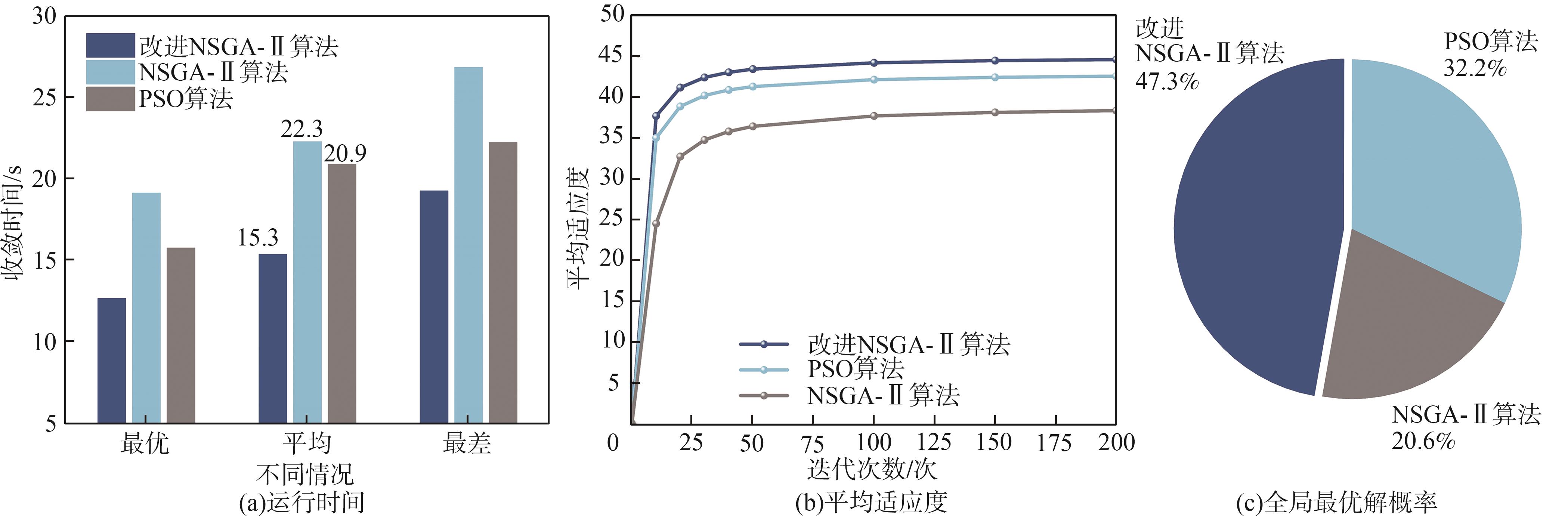
图6 算法性能对比

Fig. 6 Performance comparison of algorithms

由表2可知，本研究所提算法（改进NSGA-Ⅱ算法）在ZDT2~ZDT4基准函数上，均取得了最佳GD值，在ZDT1上虽未取得最佳GD值，但IGD值更小，表明在ZDT函数系列中，本研究所提算法相较于NSGA-Ⅱ算法、PSO算法具备更好的性能。

由图6(a)可知，改进NSGA-Ⅱ算法的收敛速度优于PSO算法和NSGA-Ⅱ算法，分别增加了31.4%和26.8%。图6(b)显示了3种算法的平均适应度。由图6(b)可知，改进NSGA-Ⅱ算法的平均适应度值可达45，优于PSO算法的平均适应度值（43）和NSGA-Ⅱ算法的平均适应度值（38），分别提高了4.7%和18.4%，表明改进NSGA-Ⅱ算法的性能优于PSO算法和NSGA-Ⅱ算法。图6(c)显示了获得全局最优解的比较概率。由图6(c)可知，改进NSGA-Ⅱ算法全局搜索能力优于PSO算法和NSGA-Ⅱ算法，PSO算法的性能优于NSGA-Ⅱ算法。综上所述，本研究所提出的算法在收敛速度以及获得全局最优解概率方面，均存在显著优势。

4.2　实例验证

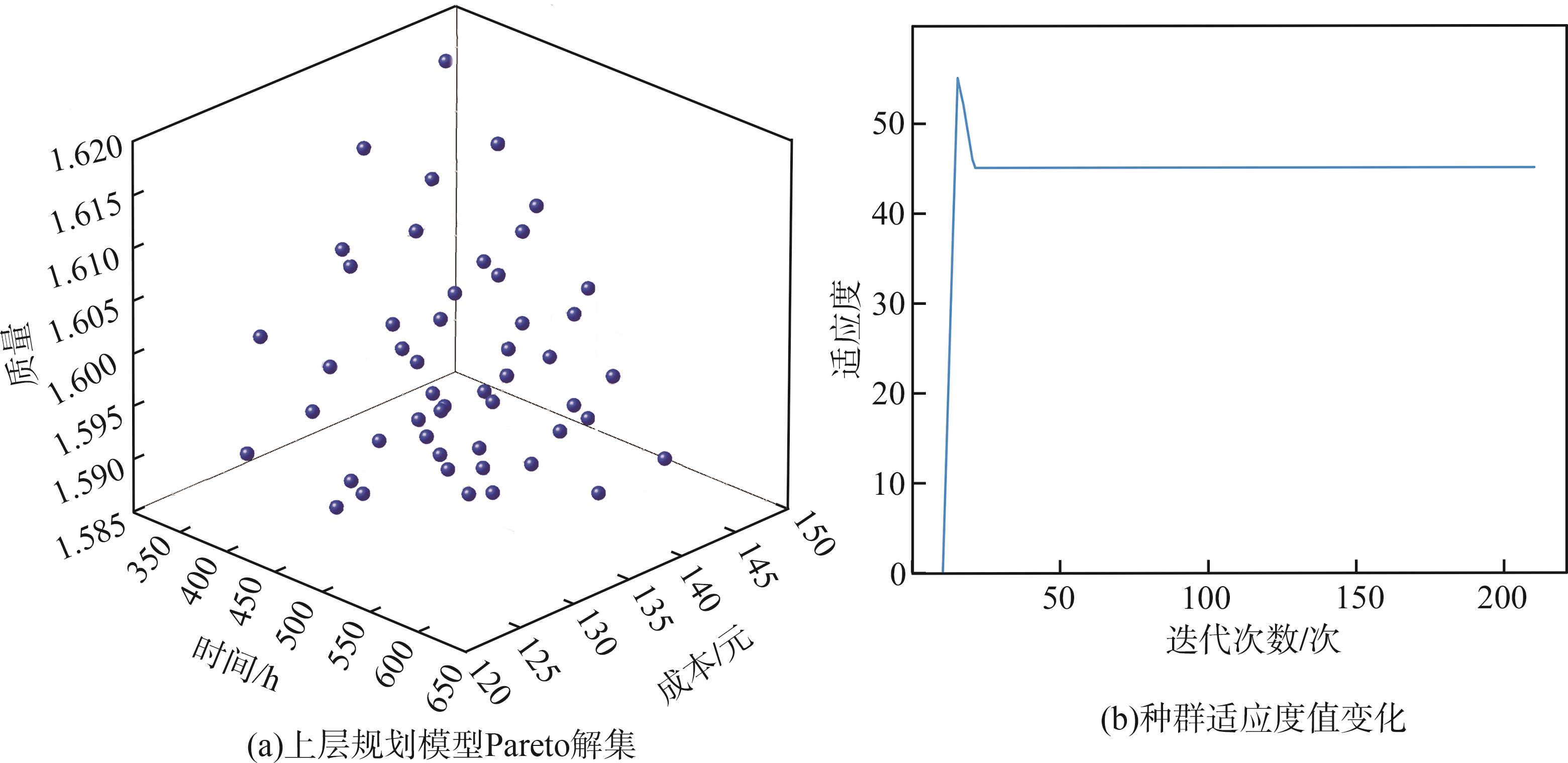
为验证所提导向辊制造服务组合优化方法的有效性，本研究采用本课题组所建立的云制造资源数据集中的导向辊制造资源数据。由式(4)可得，导向辊云制造服务组合优化双层规划模型，使用本研究的算法求解服务组合双层规划模型，最优解集的Pareto前沿和上层规划模型的适应度值变化趋势如图7所示。

图7 上层规划模型Pareto解集

Fig. 7 Pareto solution set of upper-level programming model

由图7可知，程序运行至第20代后，上层规划模型的适应度值趋于稳定。将上层优化的Pareto解集代入下层优化模型中，求得双层规划的最优解集，最优制造服务组合的QoS评价值如表3所示。由表3可知，本方法求得的最优服务组合符合预期结果。

表3 最优解排序表

Table 3 Sorting table of optimal solution

制造服务组合	T/h	C/元	Q	S	R	E
CMR₁₂-CMR₂₂-CMR₃₂-CMR₄₁-CMR₅₂-CMR₆₃-CMR₇₁	54.42	537	0.85	0.74	3.43	3.00
CMR₁₂-CMR₂₂-CMR₃₁-CMR₄₂-CMR₅₂-CMR₆₂-CMR₇₁	50.07	547	0.86	0.69	3.86	3.71

综上所述，本研究所提的双层规划模型与改进NSGA-Ⅱ算法的求解方法，在解决导向辊制造服务组合优化问题时，效果良好。

为验证本研究所提算法在处理不同需求权重偏好时，导向辊制造服务组合优化问题的能力，根据需求方对时间和成本的偏好分别设置2组不同的权重系数W₁和W₂，在W₁条件下，ω_t=0.5，ω_c=0.2，ω_q=0.3；在W₂条件下，ω_t=0.2，ω_c=0.5，ω_q=0.3。种群规模为100，交叉、变异、跳跃概率分别为0.95、0.05、0.5，最大迭代次数200，分别进行20次实验，多次实验的平均QoS属性如表4所示。

表4 不同权重条件下的实验结果

Table 4 Experimental results under different weighting conditions

权重	指标
权重	时间	成本	质量
W₁	1 801.34	621	0.851 7
W₂	2 006.73	496	0.861 0

由表4可知，在时间属性更为重要的W₁权重条件下，多次实验结果的平均时间低于W₂权重条件下的实验结果；在成本属性更为重要的W₂权重条件下，多次实验结果的平均成本远低于W₁权重条件下的实验结果，以上均符合实验预期。因此，本研究所提算法在解决不同指标权重的导向辊制造服务组合优化问题等方面具有有效性。

5 结论

本研究针对包装印刷与造纸类设备中的核心零部件导向辊，在云制造环境下的制造服务组合优化问题，分析了导向辊结构及生产制造流程，实现了导向辊制造任务的工序及任务分解，在综合考虑服务需求方、资源提供方、平台运营方三方利益的前提下，提出了综合QoS指标与柔性指标的制造服务组合评价指标体系，将双层规划思想引入导向辊制造领域，建立导向辊制造服务组合优化数学模型，并从种群初始化与遗传算子2方面对NSGA-Ⅱ算法进行改进，并完成模型求解。

基准函数测试结果表明，本研究所提出的算法相较于NSGA-Ⅱ算法与PSO算法，在绝大多数ZDT基准函数上性能更优，在收敛速度上分别提高了31.4%与26.8%，平均适应度值分别提高了4.7%与18.4%。实例验证表明了本研究所提方法，在解决不同指标权重下的导向辊制造服务组合优化问题时，均能够快速得到符合预期结果的全局最优解，验证了本研究所提算法的有效性，极大地提升了导向辊制造服务组合优化问题求解效率。

参考文献

张梦，郭大亮，童欣，等. 现代造纸企业数字化过程控制系统的研究进展［J］. 中国造纸， 2022， 41（S1）： 16-22. [百度学术]

ZHANG M， GUO D L， TONG X， et al. Research Progress of Digital Process Control System in Modern Papermaking Enterprises［J］. China Pulp & Paper， 2022， 41（S1）： 16-22. [百度学术]

李伯虎，张霖，王时龙，等. 云制造——面向服务的网络化制造新模式［J］. 计算机集成制造系统， 2010， 16（1）： 1-7. [百度学术]

LI B H， ZHANG L， WANG S L， et al. Cloud manufacturing： A new service-oriented networked manufacturing model［J］. Computer Integrated Manufacturing Systems， 2010， 16（1）： 1-7. [百度学术]

李伯虎，张霖，任磊，等. 再论云制造［J］. 计算机集成制造系统， 2011， 17（3）： 449-457. [百度学术]

LI B H， ZHANG L， REN L， et al. Further discussion on cloud manufacturing［J］. Computer Integrated Manufacturing Systems， 2011， 17（3）： 449-457. [百度学术]

JIN H， JIANG C， LYU S， et al. A hybrid teaching-learning-based optimization algorithm for QoS-aware manufacturing cloud service composition［J］. Computing， 2022， 104（11）： 2489-2509. [百度学术]

XUE X， LIU Z Z， WANG S F. Manufacturing service composition for the mass customised production［J］. International Journal of Computer Integrated Manufacturing， 2016， 29（2）： 119-135. [百度学术]

JING W， ZHAO C， MIAO Q， et al. QoS-DPSO： QoS-aware task scheduling for cloud computing system［J］. Journal of Network and Systems Management， 2021， 29： 1-29. [百度学术]

GAO J， YAN X， GUO H. A discrete manufacturing SCOS framework based on functional interval parameters and fuzzy QoS attributes using moving window FPA［J］. Concurrent Engineering， 2022， 30（1）： 46-66. [百度学术]

YUAN M， ZHOU Z， CAI X， et al. Service composition model and method in cloud manufacturing‍［J］. Robotics and Computer-Integrated Manufacturing， DOI： 10.1016/j.rcim.2019.101840. [百度学术]

SONG C， ZHENG H， HAN G， et al. Cloud edge collaborative service composition optimization for intelligent manufacturing‍［J］. IEEE Transactions on Industrial Informatics， 2022， 19（5）： 6849-6858. [百度学术]

LI T， HE T， WANG Z， et al. SDF-GA： A service domain feature-oriented approach for manufacturing cloud service composition［J］. Journal of Intelligent Manufacturing， 2020， 31： 681-702. [百度学术]

LI Y， YAO X， LIU M. Multiobjective optimization of cloud manufacturing service composition with improved particle swarm optimization algorithm［J］. Mathematical Problems in Engineering， DOI： 10.1155/2020/9186023. [百度学术]

ARUNACHALAM N， AMUTHAN A. Integrated probability multi-search and solution acceptance rule-based artificial bee colony optimization scheme for web service composition‍［J］. Natural Computing， 2021， 20： 23-38. [百度学术]

蔡安江，王艺，郭师虹，等. 蚁群BP神经网络在云制造知识服务组合优化中的应用［J］. 测试科学与仪器， 2023， 14（1）： 74-84. [百度学术]

CAI A J， WANG Y， GUO S H， et al. Application of ant colony BP network in composition optimization of cloud manufacturing knowledge service［J］. Journal of Measurement Science and Instrumentation， 2023， 14（1）： 74-84. [百度学术]

郁清. 基于改进麻雀算法的云制造服务组合优化［D］. 南京：南京邮电大学， 2023. [百度学术]

YU Q. Optimization of Cloud Manufacturing Service Composition based on Improved Sparrow Algorithm［D］. Nanjing： Nanjing University of Posts and Telecommunications， 2023. [百度学术]

DUTTA A， JATOTH C， GANGADHARAN G R， et al. QoS-aware big service composition using distributed co-evolutionary algorithm［J］. Concurrency and Computation： Practice and Experience， DOI： 10.1002/cpe.6362. [百度学术]

ZENG J， YAO J， GAO M， et al. A service composition method using improved hybrid teaching learning optimization algorithm in cloud manufacturing［J］. Journal of Cloud Computing， 2022， 11（1）： 1-14. [百度学术]

张增强. 印刷机导向辊云制造资源优化配置技术研究［D］. 西安：西安理工大学， 2023. [百度学术]

ZHANG Z Q. Research on Optimal Allocation Technology of Cloud Manufacturing Resources for Guide Roller of Printing Machine［D］. Xi’an： Xian University of Technology， 2023. [百度学术]

BRACKEN J， FALK J E， MCGILL J T. The equivalence of two mathematical programs with optimization problems in the constraints［J］. Operations Research， 1974， 22（5）： 1102-1104. [百度学术]

VELDHUIZEN V D A. Multobjective evolutionary algorithms： classifications， analyses， and new innovations［D］. Ohio： Air Force Institute of Technology， 1999. [百度学术]

COELLO C A C， SIERRA M R. A study of the parallelization of a coevolutionary multi-objective evolutionary algorithm‍［C］//MICAI 2004： Advances in Artificial Intelligence： Third Mexican International Conference on Artificial Intelligence， Mexico City， Springer Berlin Heidelberg， 2004： 688-697. [百度学术]

云制造环境下的导向辊制造服务组合优化方法

摘要

关键词

1 云制造服务组合优化问题分析

2 云制造服务组合优化评价指标体系

2.1 导向辊制造任务分解

2.2 导向辊制造服务组合优化评价指标体系

3 导向辊制造服务组合优化方法

3.1 导向辊云制造服务组合数学模型

3.2 基于NSGA-Ⅱ的模型求解方法

3.3 多目标算法评价指标