网刊加载中。。。

使用Chrome浏览器效果最佳，继续浏览，你可能不会看到最佳的展示效果，

确定继续浏览么?

复制成功，请在其他浏览器进行阅读

基于改进LADRC的放卷侧储料架张力系统建模与控制

- ORCID：
巨国力 ¹
- ORCID：
刘善慧 ¹
✉
- ORCID：
冯磊 ²
- ORCID：
李引峰 ²
- ORCID：
赵文辉 ¹

1. 西安理工大学，陕西西安，710054； 2. 陕西北人印刷机械责任有限公司，陕西渭南，714000

中图分类号： TS735⁺.1

最近更新：2024-09-20

DOI：10.11980/j.issn.0254-508X.2024.09.021

摘要

本课题针对纸张的卷对卷涂布设备，放卷侧储料架内纸张的张力控制问题，建立了储料架内纸张的张力耦合模型、输入输出辊和托架的动力学模型、滚轴丝杠的推力模型；融合遗传算法（GA）和线性自抗扰控制器（LADRC），设计了改进LADRC以实现LADRC的参数自整定和解决传统比例-积分-微分（PID）控制器控制精度不足、鲁棒性差等问题；结合所建立模型和所设计控制器，针对改进LADRC的参数整定性能和储料架内纸张的张力控制性能展开仿真实验。结果表明，所设计的改进LADRC能实现控制器的参数自整定，相比于传统PID控制器拥有更好的张力控制性能，能够满足放卷侧储料架内纸张涂布制造的张力控制需求。

关键词

纸张涂布; 卷对卷; 储料架; 改进LADRC; 张力控制

纸张是由纤维交织构成的三维网状多孔薄型材料^[

1]。纸张表面凹凸不平的性质，一方面影响纸张的表面强度和光学性能^{[参考文献 2

百度学术}2]，另一方面使纸张对水蒸气、氧气和油脂等物质的阻隔性能较差^{[参考文献 3

百度学术}3]，影响纸张的应用范围。工业上常将添加功能助剂的、具有特殊功能的涂料涂布在纸张表面，再经干燥、压光等过程，使纸张获得良好的表面性能或具有特殊功能^{[参考文献 4

百度学术}4]。卷对卷涂布设备由于其连续、绿色、大规模制造等特点，是纸张涂布制造的理想设备；其中，放卷侧储料架是卷对卷涂布设备的重要组成部分，是实现纸张连续、大规模涂布制造的关键设备。

纸张卷对卷涂布制造过程中，在放卷侧减速更换料辊时，放卷侧储料架可将储存的纸张释放出来，保证纸张卷对卷涂布制造的连续性。因此，在放卷侧储料架储存和释放纸张的过程中，储料架内纸张张力必须稳定在一个范围内，否则会影响产品质量和生产效率^[

5]。储料架的张力系统耦合模型是基于Brandenburg的双滚筒模型，在其基础上引入托架（Carriage）和输入输出辊的速度模型，及液压系统的力学模型，可以建立收卷侧速度变化时储料架的张力耦合模型；同时，基于两辊筒张力耦合模型，还可以建立线性和非线性2种不同的储料架张力耦合模型，并改进液压系统的动力学模型^{[参考文献 6-8}6-8]。收卷侧储料架与放卷侧储料架的结构组成和功能作用相似，均是为了满足卷对卷连续制造的需求，只是二者的运动过程相反。在卷对卷设备张力系统解耦控制方面，工业传统比例-积分-微分（PID）控制器在面对卷对卷设备的多输入输出系统时，存在鲁棒性差、动态裕度不足的问题。随着控制理论的不断发展，自抗扰控制器（ADRC）相比于传统PID控制器表现出了更好的鲁棒性和更高的动态裕度，能够实现对系统误差进行估计并补偿和更高的误差控制效果。线性自抗扰控制器（LADRC）与ADRC相比，结构更简单、参数整定效率更高、应用更便利，但也保留了ADRC优良的鲁棒性和动态裕度。Chen等^{[参考文献 9

百度学术}9]针对PID控制器在塑料薄膜收卷过程中张力控制精度不足的问题，采用LADRC替代传统PID控制器，仿真实验结果表明，LADRC具有优异的抗干扰性、快速性、稳定性等优点。张加语^{[参考文献 10

百度学术}10]针对涂布复合机的张力控制问题，以五辊涂布复合机为研究对象，分析比较了传统PID控制器和LADRC的张力控制性能。Fan等^{[参考文献 11

百度学术}11]针对工业储料架的控制问题，设计了一种已知模型信息的改进LADRC，仿真实验结果表明，该控制器相比于传统PID控制器拥有更好的张力控制性能，满足控制需求。虽然许多学者将LADRC应用于卷对卷设备的张力控制中，但由于LADRC参数众多，参数之间存在内部联系，导致LADRC的参数调整困难。因此，将控制器与数学算法相融合，设计能够实现控制器参数整定的改进参数自整定控制器，可以实现控制器参数的自整定。遗传算法（GA）由于计算简单、拥有全局视角和固有的并行处理，已成功应用于各类优化问题的解决，在控制器的参数整定方面也取得一定应用^{[参考文献 12-14}12-14]。

综上所述，本课题针对纸张卷对卷涂布制造过程中放卷侧储料架的张力控制问题，融合LADRC和GA，设计改进LADRC，并基于放卷侧储料架张力耦合模型进行仿真分析，具体结构如下：结合卷对卷涂布设备放卷侧储料架具体结构，建立放卷侧储料架张力耦合模型；融合GA和LADRC设计改进LADRC，实现LADRC的参数自整定；在MATLAB/Simulink中进行仿真分析，比较所设计控制器和PID控制器的控制性能。

2 储料架建模及分析

2.1　张力耦合模型

图1显示了储料架系统结构组成。在纸张卷对卷涂布制造过程中，放卷侧储料架是为了在放卷侧料辊减速停止更换料辊时，卷对卷设备能够维持正常速度，满足纸张卷对卷连续涂布制造需求。放卷侧储料架系统主要由3部分组成，即储料架、托架、摆辊。如图1(a)所示，放卷侧储料架主要由左右2排自由辊组成，在卷对卷设备放卷侧更换放卷料辊的整个过程中，放卷侧储料架通过右排自由辊的左右移动，实现纸张的释放和储存，并将储料架内纸张张力维持在一个范围内，保证纸张涂布的质量。如图1(b)所示，放卷侧储料架托架由电机提供动力，带动减速器和滚珠丝杠，实现储料架内右排自由辊的左右移动，右排自由辊的移动速度由放卷料辊和设备运行速度决定。如图1(c)所示，放卷侧储料架系统内的摆辊机构，摆辊机构一方面能够跟踪储料架内纸张张力的波动情况；另一方面，摆辊机构的存在也抑制了纸张张力的突然变化，从而可以稳定系统状态。

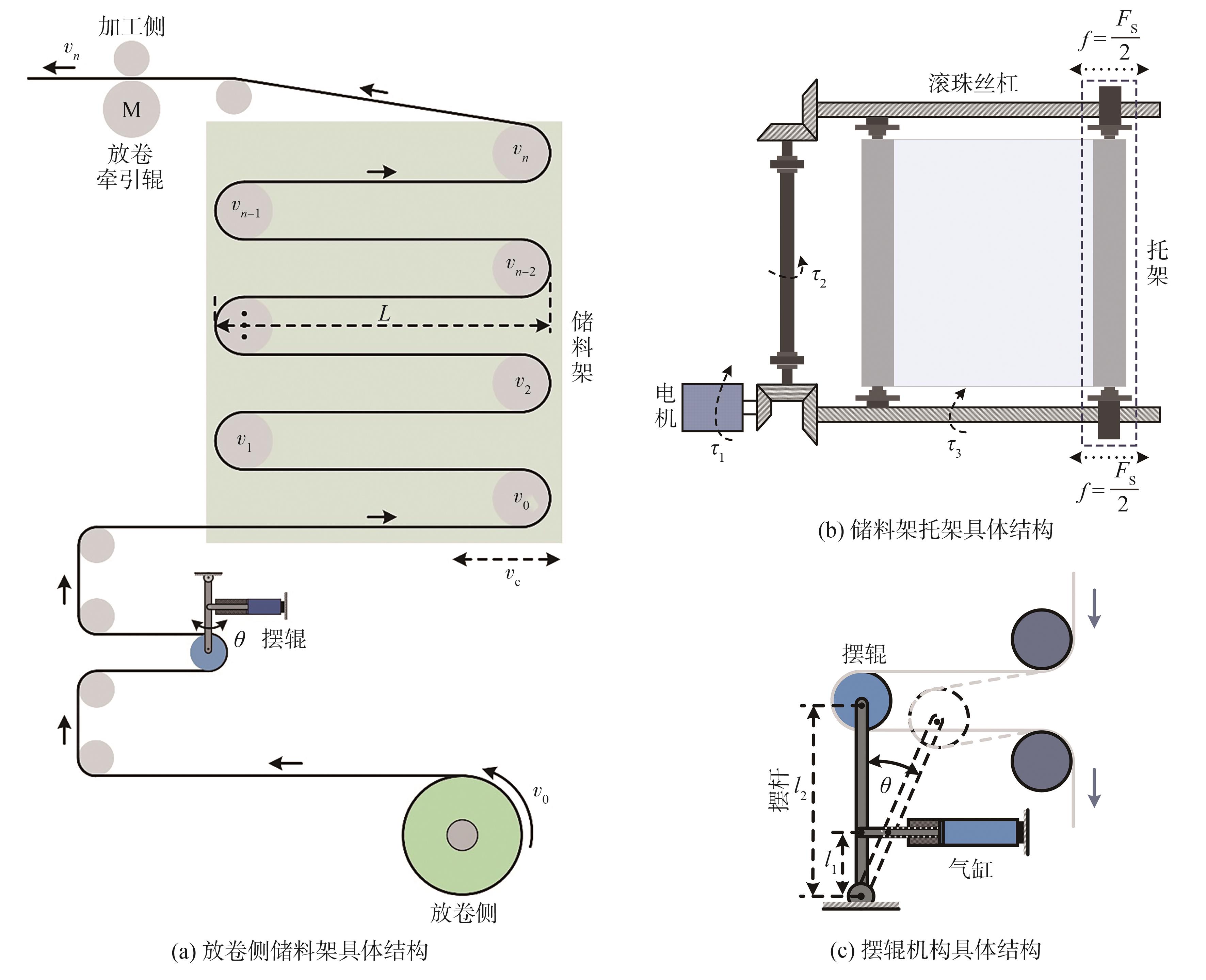
图1 储料架系统结构组成

Fig.1 Components of the accumulator system

在图1(a)所示放卷侧储料架具体结构中，储料架系统输入辊、输出辊的速度分别同放卷侧和加工侧速度相同，分别为v₀、v_n；储料架托架移动速度为v_c，左右2排自由辊间的距离为L。假设储料架内自由辊数量为n+1，纸张和各自由辊间没有滑移，储料架内自由辊线速度等于v₀、v₁、…、v_n_-1、v_n，储料架内各段纸张长度相等，均为L。根据文献[

7]，建立储料架系统的张力耦合模型如式(1)所示。

\{\begin{array}{l} \frac{d T}{d t} = \frac{1}{n} \frac{A \cdot E}{L (t)} [v_{n} (t) - v_{0} (t)] + \frac{A \cdot E}{L (t)} v_{c} (t) \\ L^{'} (t) = v_{c} (t) \end{array}

（1）

式(1)表达了v₀、v_n和v_c与储料架内纸张张力T(t)的输入输出关系，式中参数具体含义见表1。

表1 式（1）中参数含义表

Table 1 Parameter meaning table of formula(1)

参数	含义	单位
T	储料架各段纸张的张力大小	N
v₀	储料架内输入辊的线速度	m/s
v_n	储料架内输出辊的线速度	m/s
v_c	储料架内托架的移动速度	m/s
L	储料架内各段纸张长度	m
E	纸张的杨氏弹性模量	Pa
A	纸张横截面积	m²

根据文献[

12]，引入储料架输入输出辊、托架的动力学模型，如式(2)所示。

\{\begin{array}{l} v_{0}^{'} (t) = \frac{1}{J} [- f_{m} v_{0} (t) + R^{2} e (t) + J_{M} \frac{R}{R_{M}} v_{M 0} + R^{2} δ_{0}] \\ v_{n}^{'} (t) = \frac{1}{J} [- f_{m} v_{n} (t) - R^{2} e (t) + J_{M} \frac{R}{R_{M}} v_{M n} + R^{2} δ_{n}] \\ v_{c}^{'} (t) = \frac{1}{M_{c}} [F_{S} (t) - n T (t) + δ_{c}] - μ \cdot g \end{array}

（2）

式(2)中参数的具体含义见表2。

表2 式（2）中参数含义表

Table 2 Parameter meaning table of formula(2)

参数	含义	单位
f_m	轴承摩擦系数	N·m·s
J	自由辊转动惯量	kg·m²
R	自由辊半径	m
J_M	电机输出轴等效转动惯量	kg·m²
R_M	电机输出轴半径	m
v_M0，v_M_n	电机输出速度	m/s
M_c	托架质量	kg
g	重力加速度	N/kg
δ₀，δ_n，δ_c	干扰因子	N
μ	动摩擦因数
n	纸张张力段

式(2)中输出辊线速度v_n为一定值，与上游加工段线速度相同；输入辊线速度v₀跟随放卷辊线速度变化，见图2中v₀速度曲线；托架移动速度v_c跟随v₀和v_n变化，见图2中v_c速度曲线，具体计算见式(3)。

v_{c} (t) = \frac{v_{0} (t) - v_{n} (t)}{n}

（3）

图2 储料架输入辊及托架速度曲线规划

Fig. 2 Velocity profile planning for accumulator input roller and carriage

如图2所示，在更换收卷侧料辊时，v_n的变化分为8个阶段，相应的v_c的变化也分为8个阶段，每个阶段托架的运行情况如下：

1）放卷速度同加工侧速度v_n相同，托架处于初始位置，静止不动；

2）放卷速度加速上升至最大速度v_0-max，托架加速上升；

3）放卷速度保持最大速度v_0-max不变，托架匀速上升；

4）放卷速度从v_0-max减速至v_n，托架减速上升；

5）放卷速度从v_n减速至0，托架加速向下；

6）放卷速度为0，更换放料卷，托架匀速向下；

7）放卷速度从0加速至v_n，托架减速向下；

8）放卷速度同加工侧速度v_n相同，托架处于初始位置，静止不动。

2.2　摆辊和滚轴丝杠模型

摆辊系统主要由气缸、摆杆、摆辊3部分组成^[

15]，见图1(c)。储料架内纸张张力的检测依靠摆辊系统完成，当纸张张力力矩同气缸推力力矩相等时，摆杆处于平衡位置，当张力发生改变，力矩平衡状态被打破，摆杆产生θ角度偏转，并被系统内的传感器接收，根据θ计算纸张张力的动力学模型如式(4)所示^{[参考文献 16

百度学术}16]。

T (t) = \frac{1}{2 l_{2}} \{- J_{e q} \frac{d^{2} θ (t)}{d t^{2}} - f_{D} {(\frac{d θ (t)}{d t})}^{2} + l_{1} [F_{P} - k l_{1} θ (t)]\}

（4）

式(4)中参数具体含义见表3。

表3 式（4）中参数含义表

Table 3 Parameter meaning table of formula(4)

参数	含义	单位
l₁	气缸支点与摆杆连接点距离	m
l₂	摆杆长度	m
J_eq	摆辊等效转动惯量	kg·m²
f_D	轴承摩擦系数	N·m·s
F_P	气缸推力	N

式(2)中的F_S(t)为滚轴丝杠的推力，如图1(b)所示，托架是由电机配合减速器转动联轴器，联轴器配合托架两端的滚轴丝杠形成合力F_S(t)，最终带动托架左右移动。在托架的运动过程中，τ₁、τ₂和τ₃分别为电机、联轴器和滚轴丝杠的输出转矩。由于两端的滚轴丝杠由联轴器共同转动，电机在整个过程中最终形成的推力为f(t)=F_S(t)/2。根据图1(b)中的力矩转递关系可以得出电机输出转矩τ₁同滚轴丝杠输出转矩τ₃的关系，如式(5)所示。

τ_{1} = η_{1} η_{2} N_{1} N_{2} τ_{3}

（5）

滚轴丝杠推力f(t)=2πη₃τ₃/D和电机转矩τ₃=J_Msv_Ms/R_Ms，则式(5)可转换为式(6)。

f (t) = \frac{2 J_{M s} π η_{3}}{η_{1} η_{2} N_{1} N_{2} D R_{M s}} v_{M s}

（6）

式(6)表达了电机输出转速v_Ms同滚轴丝杠推力f(t)的关系，式(6)中参数具体含义见表4。

表4 式（6）中参数含义表

Table 4 Parameter meaning table of formula(6)

参数	含义	单位
D	滚轴丝杠导程	m
J_Ms	电机输出轴转动惯量	kg·m²
R_Ms	电机输出轴半径	m
η₁，η₂	齿轮传递效率
N₁，N₂	齿轮传动比
η₃	滚轴丝杠传递效率

综上所述，本节研究分析了放卷侧储料架系统的具体结构，建立了储料架系统的张力耦合模型，给出了储料架托架、输入输出辊的动力学模型，针对摆辊系统建立了摆辊系统的张力反馈模型，针对滚轴丝杠建立了滚轴丝杠的推力模型。同时，针对v₀和v_c的变化曲线，分析了储料架托架的运行情况。

3 改进LADRC

3.1　LADRC

LADRC主要由二阶线性扩张状态观测器、一阶线性误差反馈控制和根据误差对系统进行补偿3部分组成。

二阶线性扩张状态观测器的具体结构如式(7)所示。

\{\begin{array}{l} e_{E} (k) = z_{1} (k) - y (k) \\ z_{1} (k) = z_{1} (k - 1) + h [\begin{array}{l} z_{2} (k - 1) - β_{1} e_{E} (k - 1) + \\ b_{0} u (k - 1) \end{array}] \\ z_{2} (k) = z_{2} (k - 1) + h [- β_{2} e_{E} (k - 1)] \end{array}

（7）

一阶线性误差反馈控制的具体结构如式(8)所示。

\{\begin{array}{l} e_{L} (k) = y_{r e f} (k) - z_{1} (k) \\ u_{0} (k) = K_{p} e_{L} (k) \\ u (k) = [u_{0} (k) - z_{2} (k)] / b_{0} \end{array}

（8）

式(7)和式(8)中，h为系统积分步长；β₁、β₂为状态观测增益系数；b₀为误差补偿系数；K_p为误差反馈增益系数；z₁、z₂为状态估计值；y为系统输出量；y_ref为系统输入量。

3.2　遗传算法

GA算法通常以一组二进制字符串结构或浮点数编码的随机解开始搜索，每个解均被分配了一个与搜索和优化问题的目标函数直接相关的量。通过应用3个类似于自然遗传算子的算子繁殖、交叉和突变，将解的种群修改为新的种群，GA算法通过在每一代中连续应用这3个算子进行迭代工作，直到满足终止准则。本课题利用GA算法实现LADRC中K_p、β₁、β₂ 3个参数的实时整定。算法具体设置见表5，算法适应度函数J(k)采用绝对误差函数见式(9)，目标函数f(k)取适应度函数的倒数见式(10)。

\{\begin{array}{l} z_{1} (k) = z_{1} (k - 1) + h \{\begin{array}{l} h [- β_{2} e_{E} (k - 2)] - \\ β_{1} e_{E} (k - 1) + K_{p} e_{L} (k - 1) \end{array}\} \\ e (k) = z_{1} (k) - T_{r e f} (k) \\ J (k) = \int_{0}^{h} |e (k)| d t \end{array}

（9）

f (k) = \frac{1}{J (k)}

（10）

表5 GA算法具体设置

Table 5 GA algorithm specific settings

参数	种群范围	种群数量	迭代次数	编码方式	繁殖概率	交叉概率	变异概率	繁殖方式	交叉方式	变异方式
K_p	[100，300]	100	100	浮点数	0.01	0.2	0.3	精英选择	混合交叉	高斯近似变异
b₁	[100，300]	100	100	浮点数	0.01	0.2	0.3	精英选择	混合交叉	高斯近似变异
b₂	[20，800]	100	100	浮点数	0.01	0.2	0.3	精英选择	混合交叉	高斯近似变异

综上所述，本课题融合GA算法和LADRC，提出改进LADRC，实现控制器的参数自整定，控制器参数整定流程如图3(a)所示，改进LADRC结构如图3(b)所示。

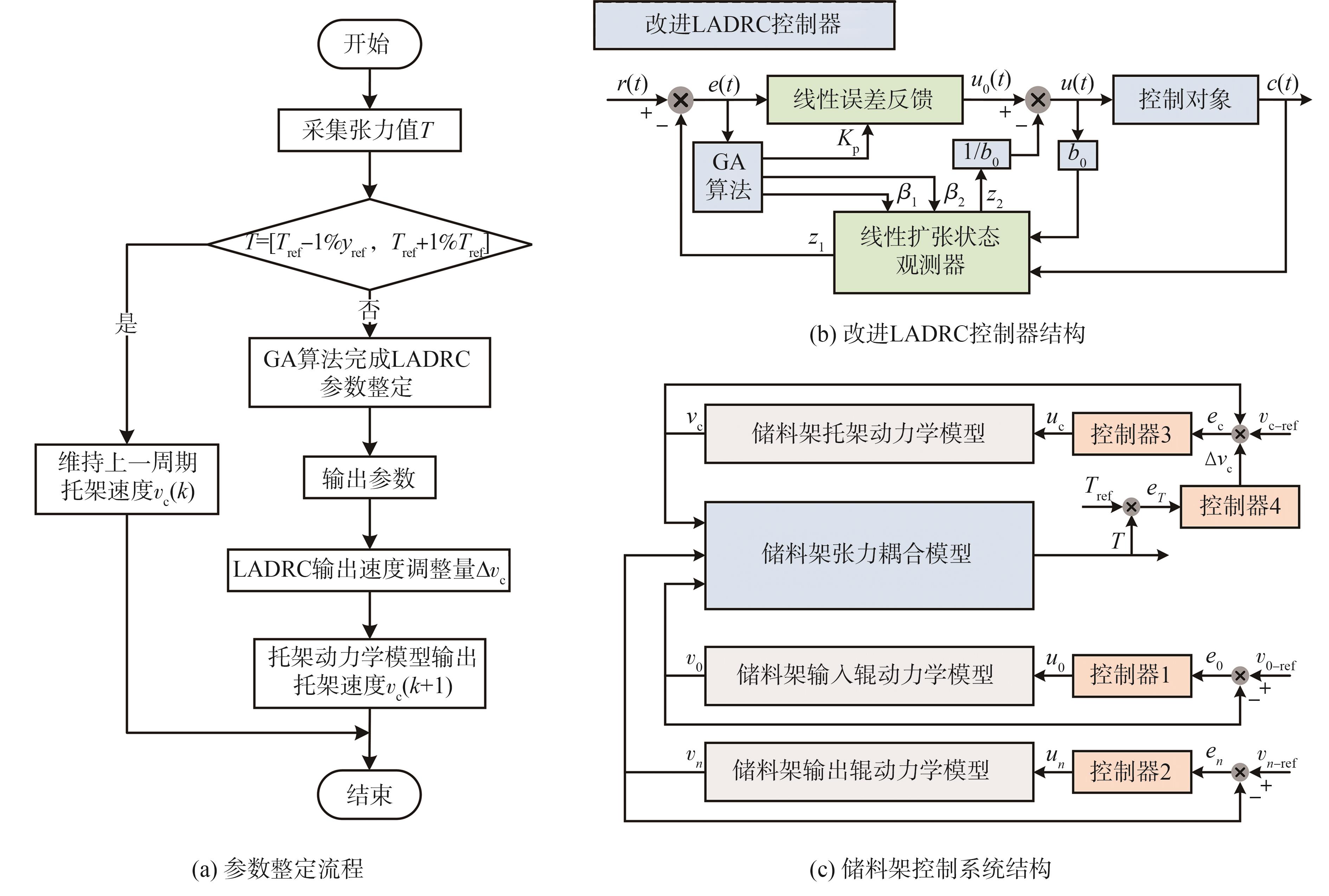
图3 控制器设置

Fig. 3 Controller settings

储料架内纸张的张力控制采用3个PID控制器与一个改进LADRC，控制器1、控制器2、控制器3采用PID控制器分别实现对储料架输出辊、输入辊、托架速度参考量v_0-ref、v_n_-ref、v_c-ref的跟踪；控制器4采用改进LADRC，其根据储料架张力反馈值输出托架速度调整量∆v_c，最终通过4个控制器的共同控制，实现储料架内纸张张力的精确控制，控制系统具体结构见图3(c)。

4 仿真分析

在建立了储料架张力耦合模型，输入输出辊、托架和摆辊机构的动力学模型，以及滚轴丝杠系统的推力模型后，本节利用所设计改进LADRC在MATLAB/Simulink（2019a）中展开仿真实验，验证改进LADRC的参数整定性能与张力控制效果。仿真步长1 ms，仿真时间200 s，v_n_-ref为2 m/s，v_0-ref、v_c-ref变化曲线见图4(a)和图4(b)，托架理想位移曲线x_c见图4(c)，储料架张力系统参考张力输入见图4(d)，仿真具体参数值见表6。

图4 参考曲线设置

Fig. 4 Reference curve setting

表6 参数具体设置

Table 6 Parameters value table

参数	数值	参数	数值
A	7×10^-6	E	7×10¹⁰
g	9.8	M_c	7 310
n	10	μ	0.05
J_R1，J_R2	0.231 4	R₀，R_n	0.2
R_M0，R_M_n，R_M_s	0.03	f_m0，f_m_n，f_D	2.25×10^-3
J_M0，J_M_n，J_M_s	0.009	J_eq	0.036
η₁，η₂	0.92	η₃	0.95
N₁	3	N₂	1
l₁	0.154	l₂	0.35
D	0.01	F_P	227.27

4.1　参数整定性能分析

参数整定性能分析针对改进LADRC在张力输出曲线不满足张力控制要求时，验证经过GA算法对初始参数整定后LADRC的张力控制情况。首先，初始化3组LADRC参数，参数值见表7；LADRC和改进LADRC分别使用3组初始化参数展开仿真实验，LADRC的张力输出曲线见图5(a)~图5(c)，改进LADRC的张力输出曲线见图5(d)~图5(f)，改进LADRC的参数变化曲线见图6(a)~图6(c)。

表7 初始化参数值

Table 7 Initial parameter setting

	K_p	β₁	β₂
第一组	50	50	625
第二组	100	50	625
第三组	100	100	2 500

图5 张力输出曲线对比图

Fig. 5 Comparison of tension output curves

图6 参数整定图

Fig. 6 Diagram of parameter self-tuning

根据图5的6组张力输出曲线，计算LADRC和改进LADRC在初始时段和175 s之后时段的最大张力超调量（over_max）和张力超调时间（t_over），结果如表8所示。由表8可知，当LADRC在使用表7中的3组初始化参数时，在初始时刻存在7.19%、5.15%、7.41%的张力超调量，超调时间为0.194、0.185、0.098 s，在175 s后时刻存在2.10%、1.29%、2.20%的张力超调量，超调时间为0.105、0.094、0.054 s；相反，改进LADRC的张力输出曲线满足张力控制要求，张力控制效果良好。上述结果表明，当储料架内张力控制精度不满足张力控制要求时，GA算法能够很好地完成LADRC的参数整定，控制器满足张力控制要求，图6展示了改进LADRC在仿真过程中的参数输出曲线。

表 8 控制性能评价表

Table 8 Evaluation table of control performance

	LADRC				改进LADRC
	初始		175 s后		初始		175 s后
	over_max/%	t_over/s	over_max/%	t_over/s	over_max/%	t_over/s	over_max/%	t_over/s
第一组	7.19	0.194	2.10	0.105	0	0	0	0
第二组	5.15	0.185	1.29	0.094	0	0	0	0
第三组	7.41	0.098	2.20	0.054	0	0	0	0

4.2　张力控制性能分析

张力控制性能分析部分围绕改进LADRC和PID控制的控制性能展开，比较传统PID控制器和本课题所设计改进LADRC的张力控制性能，采用初始仿真条件，仿真实验分为以下2部分：

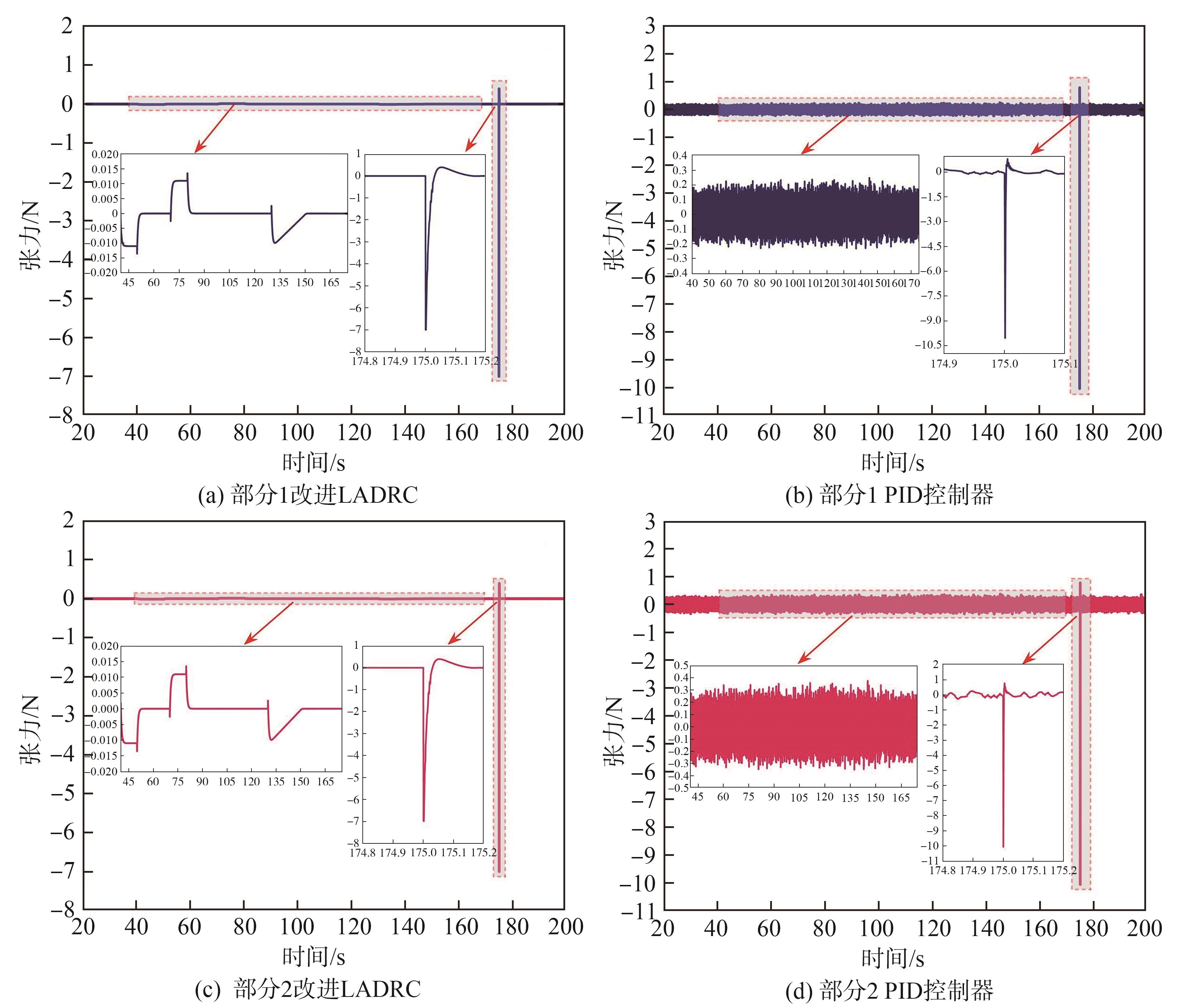
部分1：取式(2)中δ₀、δ_n、δ_c为±20 N之间的随机量，控制器4分别采用改进LADRC和PID控制器，仿真过程中的张力误差e_T₍_t₎见图7(a)和图7(b)；

图7 张力误差示意图

Fig.7 Diagram of tension error

部分2：取式(2)中δ₀、δ_n、δ_c为±30 N之间的随机量，控制器4分别采用改进LADRC和PID控制器，仿真过程中的张力误差e_T₍_t₎见图7(c)和图7(d)。

图7中4组张力输出曲线显示，当张力输出曲线在175 s时刻发生阶跃时，改进LADRC和PID控制器均存在相应的跟踪误差，但相较于PID控制器，改进LADRC的跟踪误差更小，改进LADRC的系统响应速度更快。表9展示了利用绝对平均误差（MAE）对图7中4组张力输出曲线进行张力误差评价的结果，部分1的仿真结果MAE评价中，改进LADRC的MAE为0.004 5 N，PID为0.074 5 N；部分2的仿真结果MAE评价中，改进LADRC的MAE为0.078 9 N，PID为0.183 0 N，表9中的数据表明，改进LADRC相比于PID控制器拥有更好的张力控制效果。

表9 张力误差e_T(t)评价表

Table 9 Tension error e_T(t) evaluation table ( N )

控制器	部分1	部分2
改进LADRC	0.004 5	0.078 9
PID	0.074 5	0.183 0

5 结论

本课题依据所建立放卷侧储料架模型和所设计的改进线性自抗扰控制器（LADRC），在MATLAB（2019a）中展开仿真实验。

5.1 仿真实验结果显示，LADRC在使用3组初始化参数进行张力控制时，最大张力超调量为7.41%，而改进LADRC的最大张力超调量为2.20%，

5.2 改进LADRC控制能够很好地完成控制器参数的实时调整，实现LADRC的参数自整定。

5.3 使用改进LADRC和PID控制器进行张力控制，并提取仿真过程中的张力误差e_T(t)，使用绝对平均误差（MAE）对张力误差e_T(t)进行评价，改进LADRC的2个部分的评价结果分别为0.004 5 N和0.078 9 N，PID控制器分别为0.074 5 N和0.183 0 N。

5.4 改进LADRC拥有更好的张力控制性能，能够满足纸张涂布过程中的张力控制需求。

参考文献

王益，刘寅，沈文浩. 基于X射线断层扫描技术的涂布纸张三维结构表征［J］. 中国造纸， 2023， 42（9）： 54-64. [百度学术]

WANG Y， LIU Y， SHEN W H. Three-dimensional Structural Characterisation of Coated Paper Based on X-ray Tomography［J］. China Pulp & Paper， 2023， 42（9）： 54-64. [百度学术]

王加福. 超细淀粉粒的制备及其在纸张涂布中的应用［D］. 北京：中国制浆造纸研究院， 2017. [百度学术]

WANG J F. Preparation of ultrafine starch granules and their application in paper coating ［D］. Beijing： China National Pulp and Paper Research Institute， 2017. [百度学术]

张宝军. 淀粉复合物的制备及其在纸张阻隔涂布中的应用［D］. 广州：华南理工大学， 2017. [百度学术]

ZHANG B J. Preparation of starch complex and its application in paper barrier coating ［D］. Guangzhou： South China University of Technology， 2017. [百度学术]

尤鹏，杨仁党，杨飞，等. 专用防水剂在纸张涂布中的应用［J］. 中国造纸， 2008，27 （4）： 24-26. [百度学术]

YU P， YANG R D， YANG F， et al. Application of Special Waterproofing Agent in Paper Coating［J］. China Pulp & Paper， 2008，27（4）：24-26. [百度学术]

张飞. 造纸机恒张力控制系统研究［D］. 长沙：中南大学， 2013. [百度学术]

ZHANG F. Research on constant tension control system for paper machine［D］. Changsha： Central South University， 2013. [百度学术]

BRANDENBURG G. New mathematical models and control strategies for rotary printing presses and related web handling systems［J］. IFAC Proceedings Volumes， 2011， 44（1）： 8620-8632. [百度学术]

PAGILLA P R， SINGH I， DWIVEDULA R V. A study on control of accumulators in web processing lines［J］.Journal of Dynamic Systems， Measurement， and Control， 2004， 126（3）： 453-461. [百度学术]

KUHM D， KNITTEL D. New mathematical modelling and simulation of an industrial accumulator for elastic webs［J］. Applied Mathematical Modelling， 2012， 36（9）： 4341-4355. [百度学术]

CHEN M X， LU P P， ZHANG H. Linear Active Disturbance Rejection Control Strategy of Plastic Film Winding Tension［J］. Engineering Plastics Application， 2021， 49（8）：74-80. [百度学术]

张加语. 基于线性自抗扰的涂布复合机张力与速度控制［D］. 上海：上海交通大学， 2019. [百度学术]

ZHANG J Y. Tension and speed control of coating and laminating machine based on linear self-immunity ［D］. Shanghai： Shanghai Jiao Tong University， 2019. [百度学术]

FAN Y， WANG Z， XIONG J. Tension control for an industrial accumulator based on linear active disturbance rejection control［C］//The 26th China Process Control Conference.Process Control Committee of the Chinese Society of Automation， 2015：1. [百度学术]

PAGILLA P R， GARIMELLA S S， DREINHOEFER L H， et al. Dynamics and control of accumulators in continuous strip processing lines［J］. IEEE Transactions on Industry Applications， 2001， 37（3）： 934-940. [百度学术]

李艳，王素方，万芙蓉. 基于遗传算法的碱回收炉炉膛负压模糊-PI复合控制［J］. 中国造纸学报， 2016， 31（3）： 36-41. [百度学术]

LI Y， WANG S F， WAN F R. Fuzzy-PI Composite Control of Negative Pressure in Alkali Recovery Furnace Chamber Based on Genetic Algorithm［J］. Transactions of China Pulp and Paper， 2016， 31（3）： 36-41. [百度学术]

JU G， LIU S， WEI K， et al. A Parameter Self-tuning Decoupling Controller Based on an Improved ADRC for Tension Systems［J］. Applied Sciences， DOI： 10.3390/app131911085. [百度学术]

刘善慧，王子煜，习大润，等. 卷筒料精密涂布机张力系统耦合建模与分析［J］. 西安理工大学学报， 2022， 38（4）： 526-532. [百度学术]

LIU S H， WANG Z Y， XI D R， et al. Coupled modelling and analysis of the tension system of a web precision coater［J］. Journal of Xi’an University of Technology， 2022， 38（4）： 526-532. [百度学术]

WANG Z Y， LIU S H， FENG L， et al. Coupling Modeling and Analysis of the Tension System for Roll-to-roll Gravure Printing Machines［J］. Journal of Imaging Science and Technology， DOI： 10.23521J.Imaging Sci.Technol.2022.66.2.020401. [百度学术]

基于改进LADRC的放卷侧储料架张力系统建模与控制

摘要

关键词

2 储料架建模及分析

2.1 张力耦合模型

2.2 摆辊和滚轴丝杠模型

3 改进LADRC

3.1 LADRC

3.2 遗传算法