网刊加载中。。。

使用Chrome浏览器效果最佳，继续浏览，你可能不会看到最佳的展示效果，

确定继续浏览么?

复制成功，请在其他浏览器进行阅读

融合LPA*和DWA算法的导向辊生产车间AGV组合路径规划方法研究

- ORCID：
刘嘉琪 ¹
- ORCID：
刘善慧 ¹
✉
- ORCID：
任慧冉 ¹
- ORCID：
陈宇宏 ²
- ORCID：
季海阳 ¹

1. 西安理工大学，陕西西安，710048； 2. 富联精密电子（郑州）有限公司，河南郑州，450000

中图分类号： TS734

最近更新：2024-06-21

DOI：10.11980/j.issn.0254-508X.2024.06.020

摘要

针对造纸类机械的导向辊生产线存在的多车间室内外导航精度不足、多车间运输通道共用、单车间产线交叉等问题，提出了融合LPA*和DWA算法的导向辊生产车间自动引导车（Automated Guided Vehicle，AGV）组合路径规划方法。首先建立了AGV本体运动模型和导向辊生产车间模型；然后提出了局部与全局组合的路径规划方法，采用LPA*算法进行全局路径规划解决了全局最优路径的问题，采用DWA算法进行局部路径规划解决了避障问题；最后通过实验验证将本研究提出的组合路径规划算法与传统路径规划算法对比，组合路径规划算法较大缩短了路径搜索的时间，效率更高。

关键词

造纸类机械; 导向辊生产车间; AGV; 路径规划

导向辊作为造纸类机械中种类最多、需求量最大的零部件之一，被广泛应用于造纸工业和包装印刷工业的纸张、薄膜等材料的传输中，其自动化加工水平直接影响造纸类机械的生产效率^[

1]。然而，我国造纸类机械制造企业的导向辊生产车间依然采用人工开叉车的方式进行物料运输，存在自动化水平低、人力成本高等问题^{[参考文献 2

百度学术}2]。目前自动引导车（Automated Guided Vehicle，AGV）已经广泛应用于不同的制造行业，因此，在导向辊生产车间中应用AGV是提高生产效率、降低人力成本的有效途径，而高效且精确的路径规划是其在导向辊生产车间中应用的前提和保障。

AGV的路径规划难点在于难以获得较高精度的AGV当前位姿及如何根据环境需要改变规划路径^[

3]。目前，AGV的路径规划主要分为全局路径规划和局部路径规划^{[参考文献 4

百度学术}4]，全局路径规划算法主要有可视图法、单元分解法^{[参考文献 5

百度学术}5]、神经网络^{[参考文献 6

百度学术}6]、蚁群算法、遗传算法、栅格法^{[参考文献 7

百度学术}7]等；局部路径规划算法有人工势场法^{[参考文献 8

百度学术}8]、粒子群优化^{[参考文献 9

百度学术}9]等。目前，栅格法是一种广泛应用于实践的路径规划方法，由于其计算简单、易于编程等优势，许多学者们基于栅格法提出了各种经典算法，常见的有A*算法^{[参考文献 10

百度学术}10]、Dijkastra算法^{[参考文献 11

百度学术}11]、D*算法^{[参考文献 12

百度学术}12]、D*Lite算法^{[参考文献 13

百度学术}13]、JPS算法^{[参考文献 14

百度学术}14]和LPA*算法^{[参考文献 15

百度学术}15]等。黄程侃^{[参考文献 16

百度学术}16]通过对JPS算法进行剪枝优化，减少JPS算法在运行过程中的计算节点，提高计算速度。李生等^{[参考文献 17

百度学术}17]将LPA*算法应用于虚拟人的路径规划中，通过对LPA*算法进行改性，改性LPA*算法更加适用于复杂维修环境，相较于传统LPA*算法其能规划出额外可行的路径。Zhang等^{[参考文献 18

百度学术}18]以目标距离代替DWA算法中方向差的评价项，避免了路径因振动而运行不平滑的现象。

目前在进行AGV的路径规划时仍存在多种问题，以导向辊生产车间为例，其存在多车间室内外导航精度不足、多车间运输通道共用、单车间产线交叉等问题，导致AGV在工作时路径规划效率不高。因此，为了解决上述问题，本研究提出了融合LPA*算法和DWA算法的导向辊生产车间AGV组合路径规划方法，缩短路径规划的时间，提高AGV物料运输的效率。

1 导向辊生产线车间建模

1.1　AGV运动模型

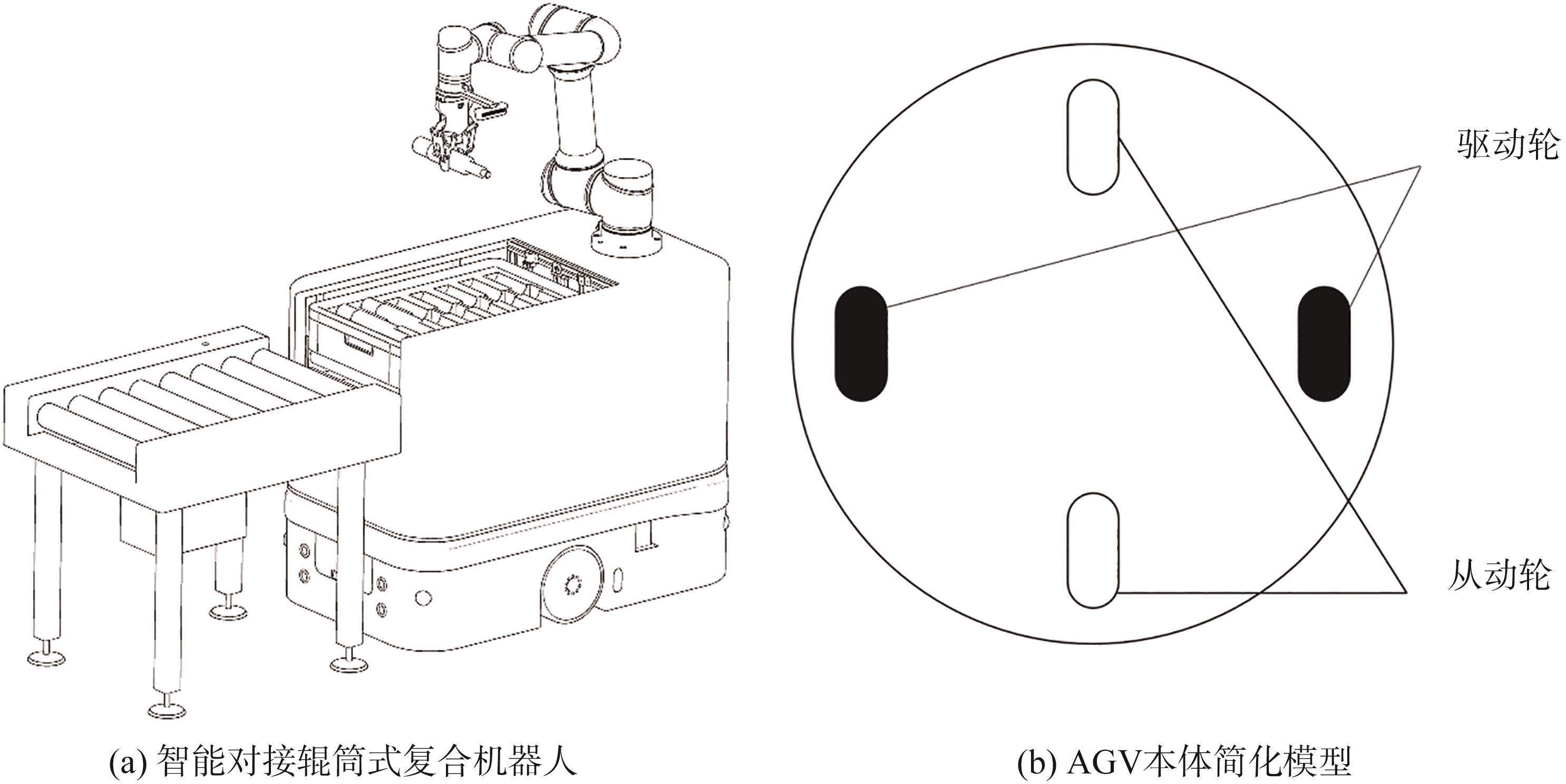
目前多数造纸及印刷企业导向辊生产线中，存在下料车间到主体加工车间的室内外导航精度不足、下料车间到主体加工车间与墙板原料到墙板加工车间物料运输通道共用、导向辊主体加工车间辊筒加工与装配产线交叉等问题。针对此现象，本研究设计了一种智能对接辊筒式复合机器人，以实现多种对接高度并独立完成物料的运输，其结构示意图如图1所示。由图1(b)可知，AGV由主动轮和从动轮组成，主动轮差速运行便可实现AGV的旋转。

图1 智能移动机器人简图

Fig. 1 Intelligent mobile robot schematic

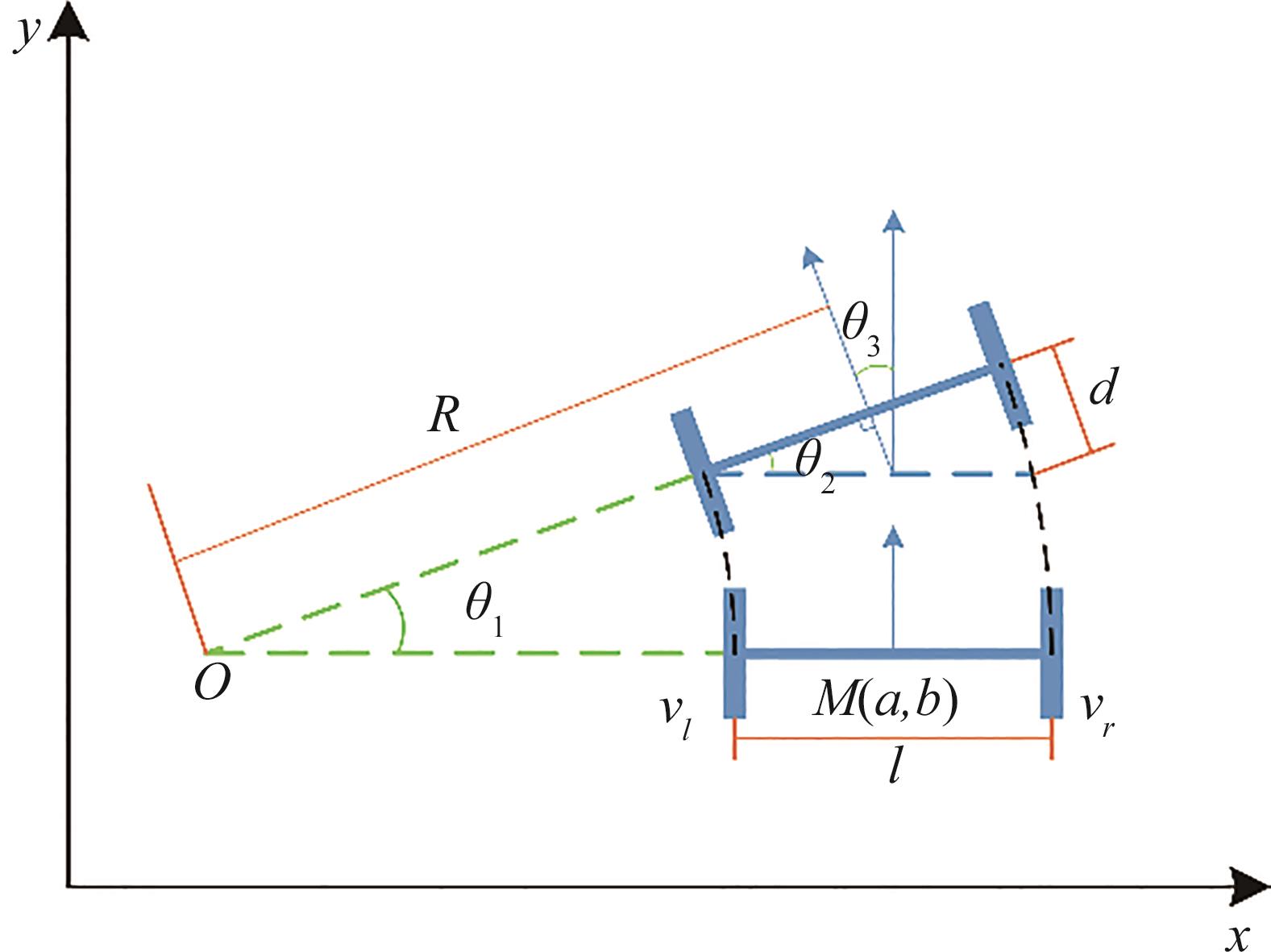
假设车身质量均匀，车的中心位于底座中心，且忽略车轮摩擦，可建立如图2所示的AGV运动模型。从图2可以看出，在坐标系中设两驱动轮的中心点位坐标为M(a,b)，w表示角速度，rad/s；v表示线速度，m/s；n表示驱动轮的转速，r/min；l表示两轮间距，m；d表示两轮中心距，m；R表示驱动轮的轮半径，m；v_r表示AGV右轮某时刻瞬时速度，m/s；v_l表示AGV左轮某时刻瞬时速度，m/s。从起始时刻到t时刻，AGV位姿发生变化为（ $x_{t}, y_{t}, θ_{t}$ ）。

图2 AGV运动模型

Fig. 2 Motion model of AGV

AGV的运动模型可表示为式(1)。

[\begin{matrix} x \\ y \\ θ \end{matrix}] = [\begin{matrix} a \\ b \\ θ_{0} \end{matrix}] + [\begin{matrix} c o s θ_{t} & - s i n θ_{t} & 0 \\ s i n θ_{t} & c o s θ_{t} & 0 \\ 0 & 0 & 1 \end{matrix}] [\begin{matrix} π R (n_{r} + n_{l}) \\ 0 \\ \frac{π R (n_{r} - n_{l})}{d} \end{matrix}] Δ t

（1）

由式(1)可知，通过控制左右两驱动轮的转速就能够实现对AGV的运动控制。

1.2　导向辊生产车间模型构建

某印刷装备制造企业导向辊生产线由导向辊主体加工车间、微弧氧化车间、下料车间和墙板生产车间组成，其中导向辊主体加工车间由铝堵加工单元、钢轴加工单元、导向辊装配单元、辊筒加工单元和导向辊精加工单元组成，导向辊生产车间平面图如图3所示。

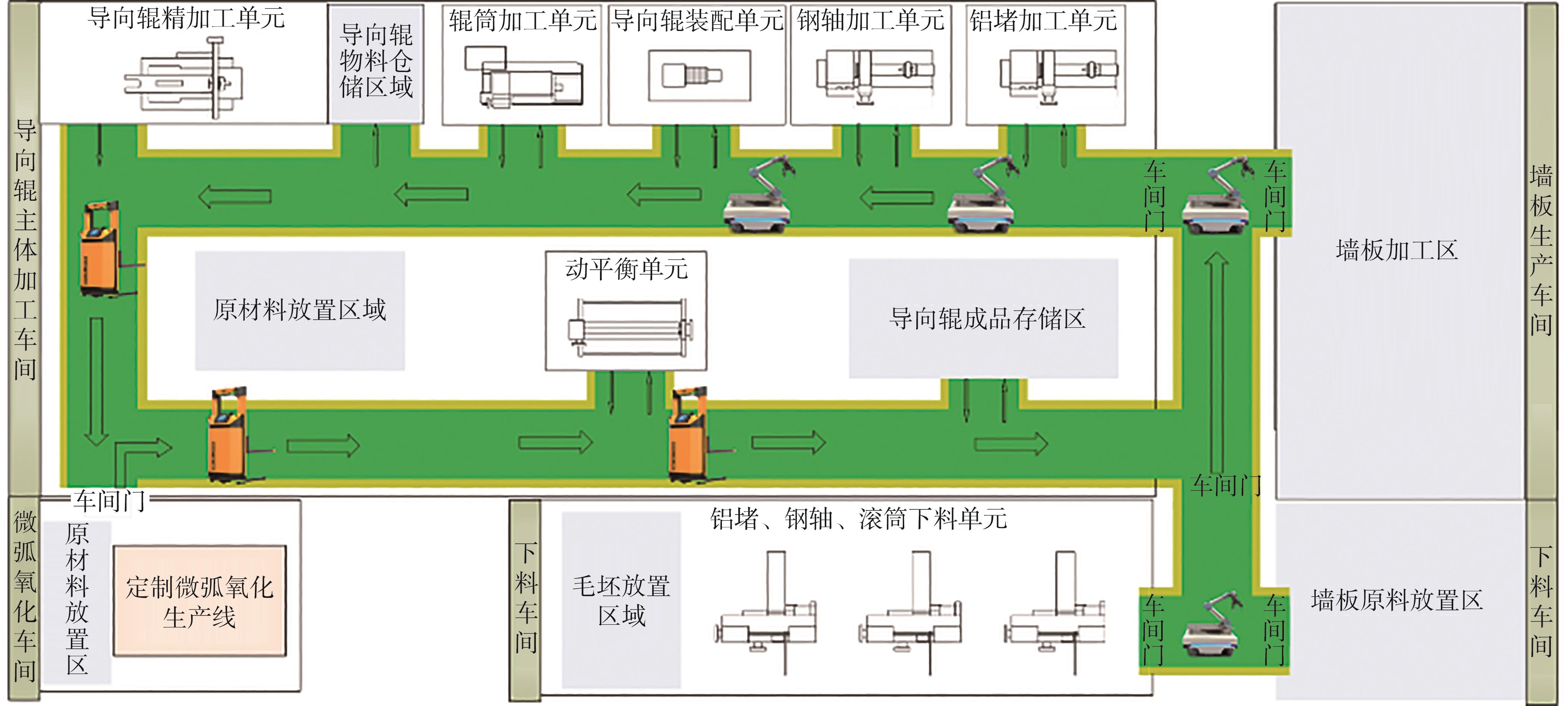
图3 导向辊生产车间平面图

Fig. 3 Guide roller production workshop plan

对构建的三维模型进行三维渲染并转换为DAE格式进行输出，结果如图4所示。

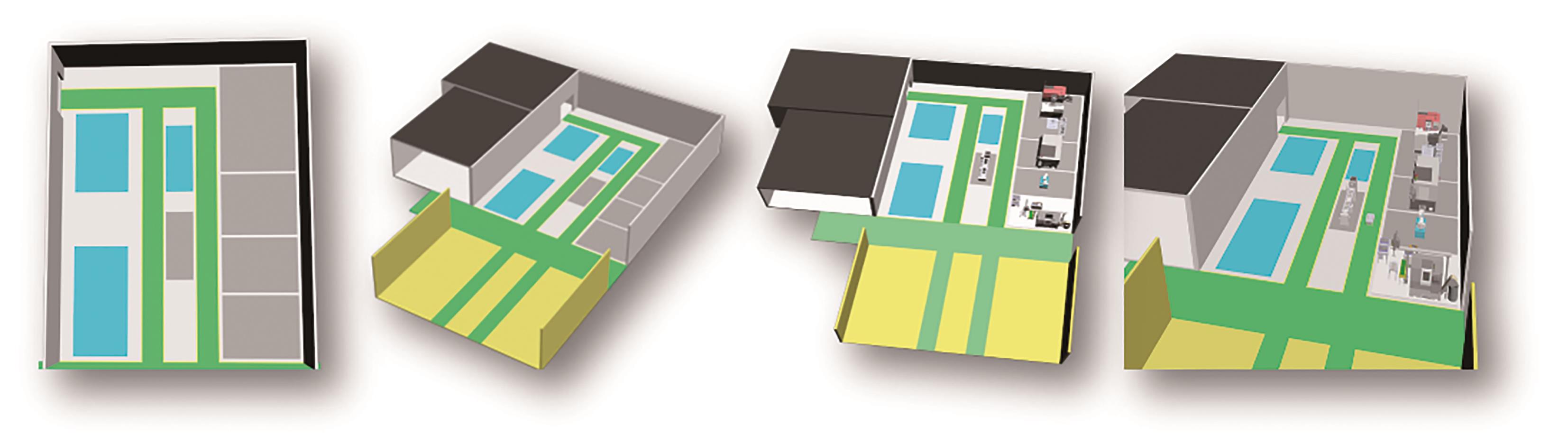
图4 车间三维渲染模型

Fig. 4 3D rendering model of workshop

将保存DAE格式的车间模型导入到ROS系统里进行编译并调用，将车间模型导入到Gazebo里进行仿真，同时打开RVIZ可视化软件实时观察车间仿真模型的情况。车间模型在RVIZ和Gazebo中的显示情况如图5所示。

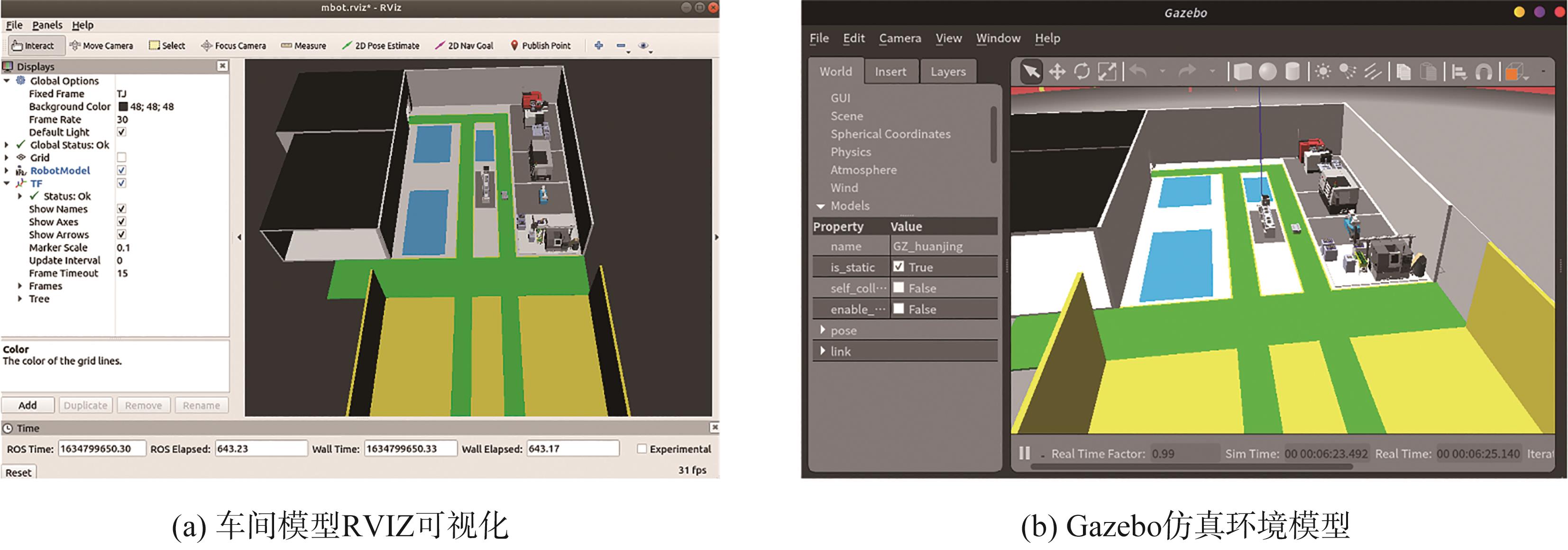
图5 仿真空间的车间模型图

Fig. 5 Workshop model of the simulation space

2 导向辊生产线车间AGV路径规划方法

针对导向辊生产车间人员流动大、机器设备多、移动物体多变等问题，本研究提出局部与全局组合的路径规划方法，将整个车间行驶区域的路径规划进一步划分为局部和全局路径规化，在局部路径规化需要解决避障的问题，在全局路径规化中需要解决最优路径的问题。导向辊生产车间物料运输AGV路径规划总体框架如图6所示。

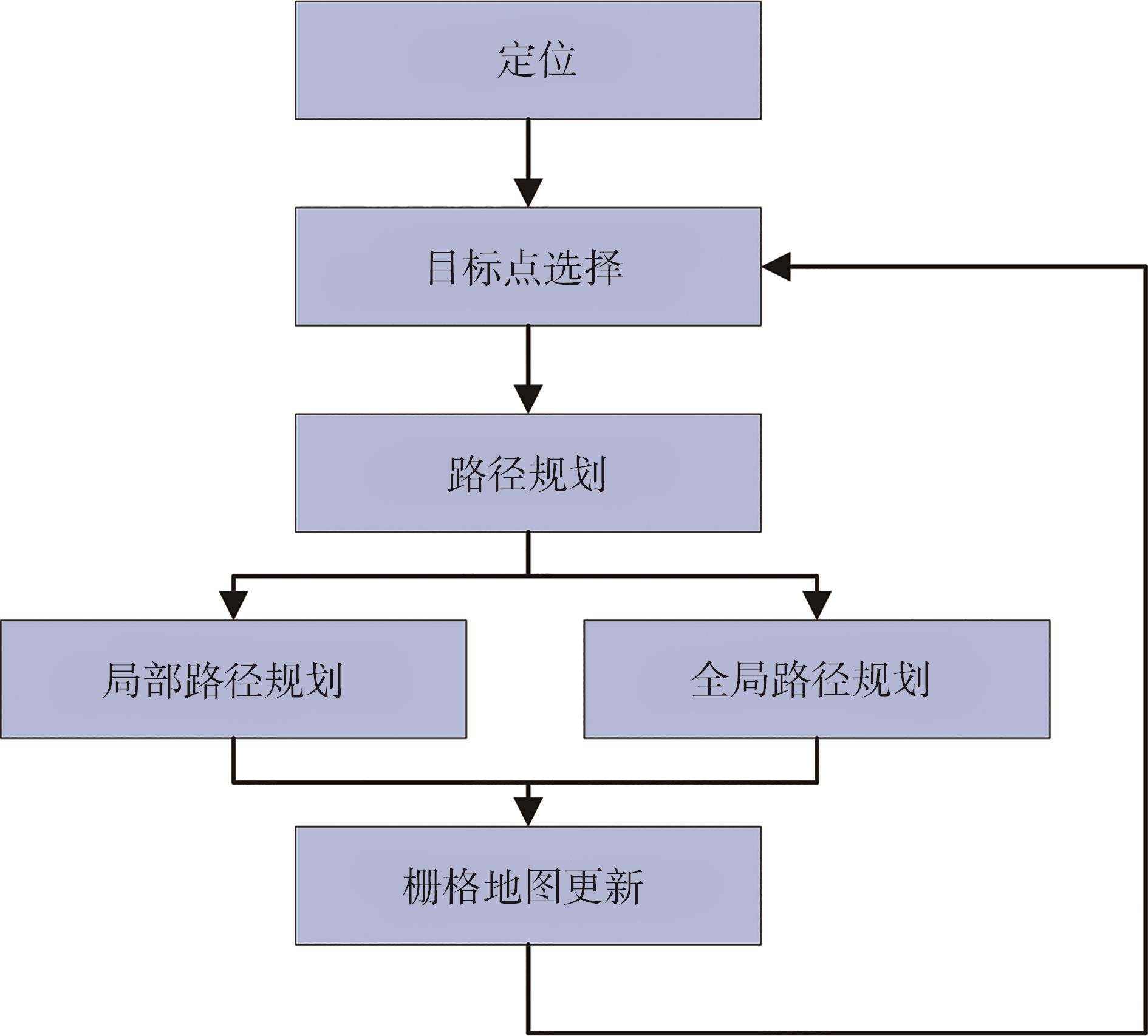
图6 AGV路径规划总体框架

Fig.6 Overall framework of AGV path planning

2.1　局部路径规划算法设计

局部路径规划的任务是将全局路径规划得到的路径转变为速度控制命令，再发送给机器人执行。通过应用DWA算法，有效地解决复杂的局部路径规划问题。通过采样速度空间，DWA算法可以模拟不同速度下的运动轨迹，并利用评估函数来确定最佳的运动轨迹，从而达到最优的运动效果。

在DWA算法中，需要建立机器人的运动模型，进而模拟机器人的运动轨迹。本研究的机器人使用双轮差速结构，其运动模型可表示为式(2)。

\{\begin{array}{l} v = \frac{r_{L} {\dot{φ}}_{L}}{2} + \frac{r_{R} {\dot{φ}}_{R}}{2} \\ w = \frac{r_{R} {\dot{φ}}_{R}}{l} - \frac{r_{L} {\dot{φ}}_{L}}{l} \end{array}

（2）

式中，r_L和r_R分别表示机器人左、右轮径，m。基于该运动模型，可以根据速度推算机器人的航迹，见式(3)。

\{\begin{array}{l} x_{t} = x_{t - 1} + v_{t - 1} Δ t c o s (θ_{t - 1}) \\ y_{t} = y_{t - 1} + v_{t - 1} Δ t s i n (θ_{t - 1}) \\ θ_{t} = θ_{t - 1} + w Δ t \end{array}

（3）

式中， $x_{t}$ 表示机器人在t时刻的横坐标位置； $y_{t}$ 表示机器人在t时刻的纵坐标位置； $θ_{t}$ 表示机器人在t时刻的朝向角度，rad。

利用对速度的采样获取机器人的运动轨迹，并使用评估函数来衡量其精确性和可靠性，速度采样的受限范围见式(4)。

\{\begin{array}{l} (v_{m}, w_{m}) = \{\begin{array}{l} v_{m} \in [v_{m i n}, v_{m a x}], \\ w_{m} \in [w_{m i n}, w_{m a x}] \end{array}\} \\ (v_{d}, w_{d}) = \{\begin{array}{l} v_{d} \in [v_{c} - a_{m a x} Δ t, v_{c} + a_{m a x} Δ t], \\ w_{d} \in [w_{c} - α_{m a x} Δ t, w_{c} + α_{m a x} Δ t] \end{array}\} \\ (v_{a}, w_{a}) = \{\begin{array}{l} v_{a} \leq \sqrt[]{2 d i s t (v, m) a_{m a x}}, \\ w_{a} \leq \sqrt[]{2 d i s t (v, m) w_{m a x}} \end{array}\} \end{array}

（4）

式中，(v_m, w_m)表示受机器人的速度约束构建可行的速度空间；(v_min, v_max)表示机器人的最小线速度和最大线速度，m/s；(w_min, w_max)表示机器人的最小角速度和最大角速度，rad/s；(v_d, w_d)表示当前运动过程中最大的加速度约束下，机器人在固定时间段t的速度变化窗口；v_c和w_c表示当前机器人的线速度（m/s）和角速度（rad/s）；α_max表示机器人的最大加速度（m/s²）和最大角加速度（rad/s²）；v_α和w_α表示保证机器人能够在碰撞到障碍物前以最大加速度停下的速度空间；dist(v, m)是机器人速度配置对应的轨迹到障碍物的最小距离，m。

通过速度采样，获得了可行的速度空间。需要对这些速度空间进行评估，选择最优的速度控制指令，评估函数见式(5)。

\begin{array}{l} e v a l u a t i o n (v, w) = α \cdot h e a d i n g (v, w) + β \cdot d i s t (v, w) + \\ γ \cdot v e l o c i t y (v, w) \end{array}

（5）

式中，heading(v, w)表示机器人速度方向与目标点方向的夹角，rad；dist(v, w)表示机器人速度配置(v, w)对应的轨迹到障碍物的最小距离（m），以保证机器人轨迹无碰撞；velocity(v, w)表示机器人的速度（m/s），保证机器人以最大速度运动；α, β, γ分别表示评估函数的权重。

2.2　全局路径规划算法设计

在确定目标点后，机器人需要规划从当前位置到目标点的路径，具体来说，全局路径规划是在栅格地图中找到一条从起始点到目标点的最优路径，即要求路程尽量短、容易控制。本研究采用的全局路径规划LPA*算法属于基于图的启发式搜索算法，在使用搜索算法前，需要先进行网格绘制。

LPA*算法从第一个网格S_start开始向下扩展，直到扩展到最后一个网格S_end或者向下没有可扩展的网格为止。LPA*算法中存在优先级函数k(s)，其定义如式(6)~式(8)所示。

k (s) = [k_{1} (s); k_{2} (s)]

（6）

k_{1} (s) = m i n (g (s), r h s (s)) + h (s)

（7）

k_{2} (s) = m i n (g (s), r h s (s))

（8）

式中，g(s)表示从S_start到s的各种损失，rhs(s)是g(s)的一步前瞻估计值，即在扩展到s点前的一个前瞻损失。rhs(s)的定义如式(9)所示。

r h s (s) = \{\begin{array}{l} 0, s = S_{s t a r t} \\ m i n_{s} \in p r e d (s) (g (s ’) + c (s ’, s)) 其他 \end{array}

（9）

式中，c(s’，s)表示从s网格到达s’网格的损失，pred(s)是s的路径直接前驱的集合。当g(s)>rhs(s)时，认为网格s是过一致的；当g(s)<rhs(s)时，认为网格s是欠一致的；当g(s)=rhs(s)时，认为网格s是一致的。

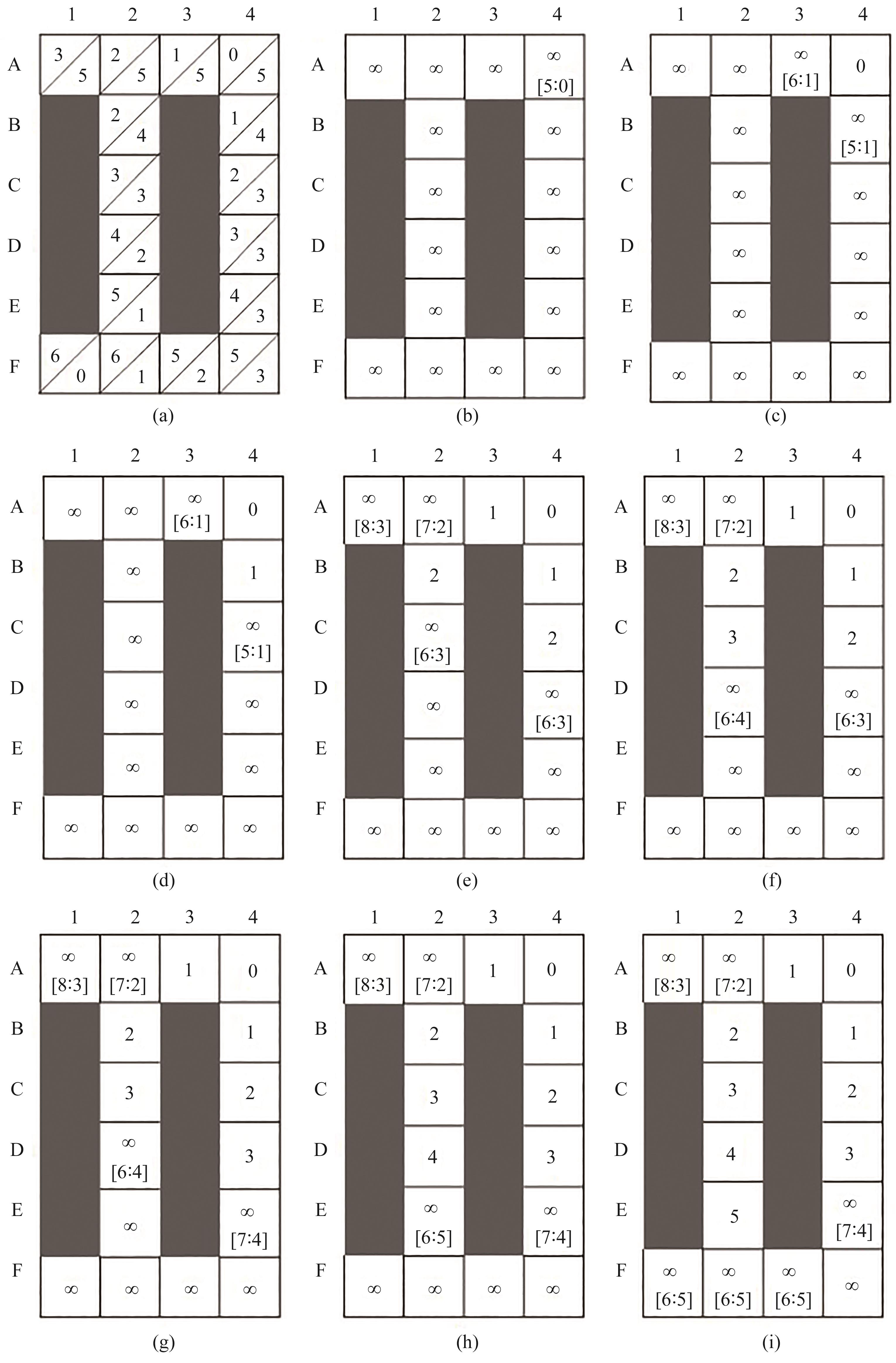
图7为LPA*算法栅格地图。从图7可以看出，假设起始点为A4，目标点为F1，1个方格代表1个栅格，栅格左上角数字代表这个点到起始点的最小代价值g*，栅格右下角数字表示这个点到目标点的估计代价h。对整个栅格进行赋值如图7(a)所示。定义所有的节点rhs和g值均为无穷，从起始点出发将起始点的rhs设置为0，因为A4的rhs和g值不相等，导致变为局部不一致状态，将A4放入到优先队列中进行重新评估，同时得到A4栅格的k值如图7(b)所示。然后以A4作为父节点，此时的rhs<g值；令g值=rhs，遍历A3附近的8个方向子节点，执行如图7(c)所示，此时A3、B4的rhs≠g，同理，将其放入优先队列里，得到相应的k值，把k值最小的节点作为新的父节点。

图7 LPA*算法栅格地图

Fig. 7 Raster map with LPA* algorithm

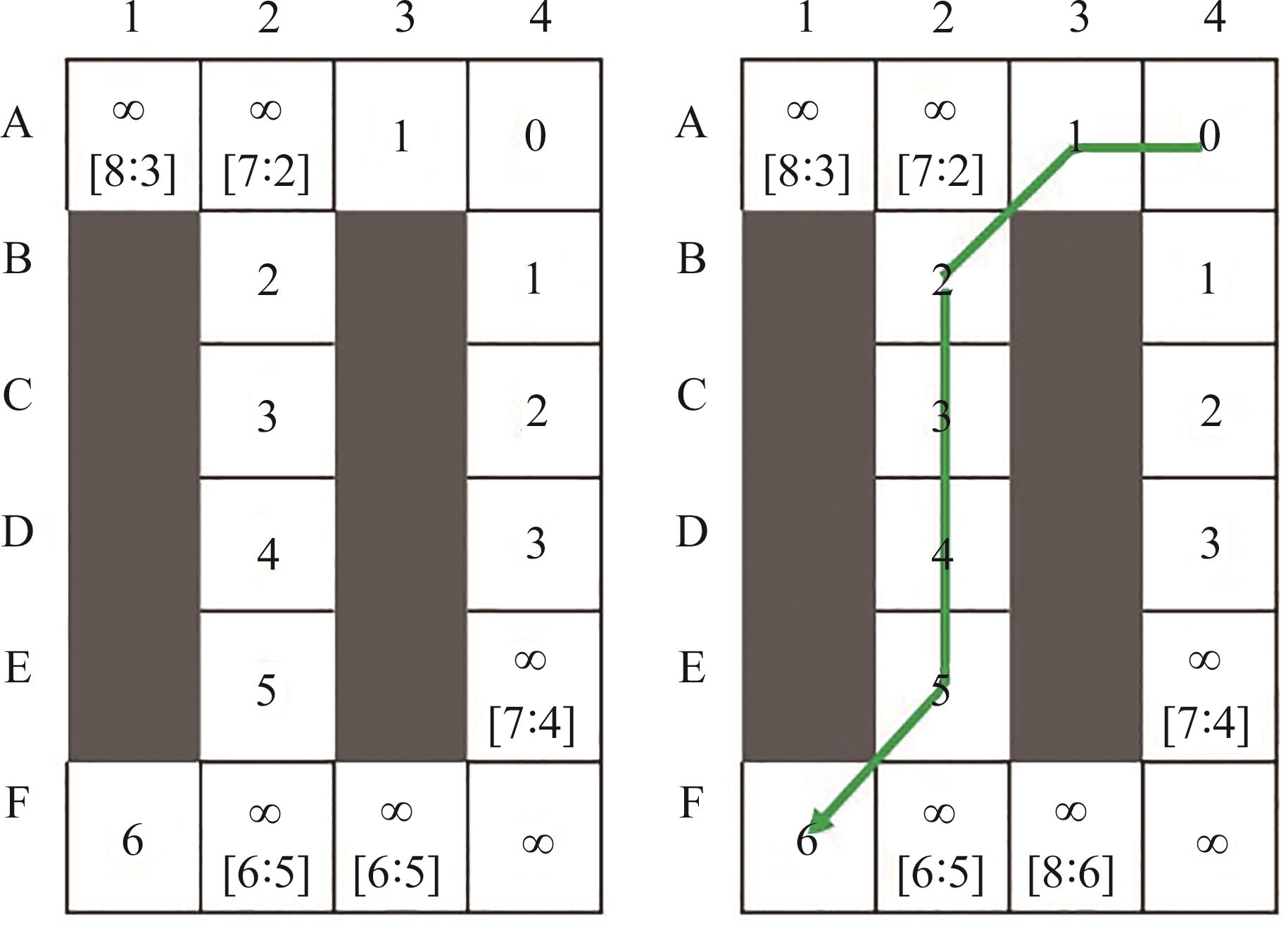
把B4作为k值最小节点选取出来，如图7(d)所示，按照步骤选取C4、C2、D4、D2、E2作为父节点，同时更新节点信息如图7(e)~图7(i)所示。当优先队列的最小k值大于目标点，或目标点的rhs与g值相等且不为无穷时结束循环，见图8。由图8可知，从目标点反推每个子节点的父节点，直至到达起点位置，将这些父节点连接起来就构成了路径，规划出的路径为最短路径。

图8 LPA*算法规划栅格地图

Fig. 8 Raster map planned by LPA* algorithm

使用MATLAB对LPA*算法的路径规划过程进行仿真，在栅格地图中，黑色表示障碍物，白色表示可通行区域，黄色和红色分别为起始点和目标点，规划结果如图9所示。

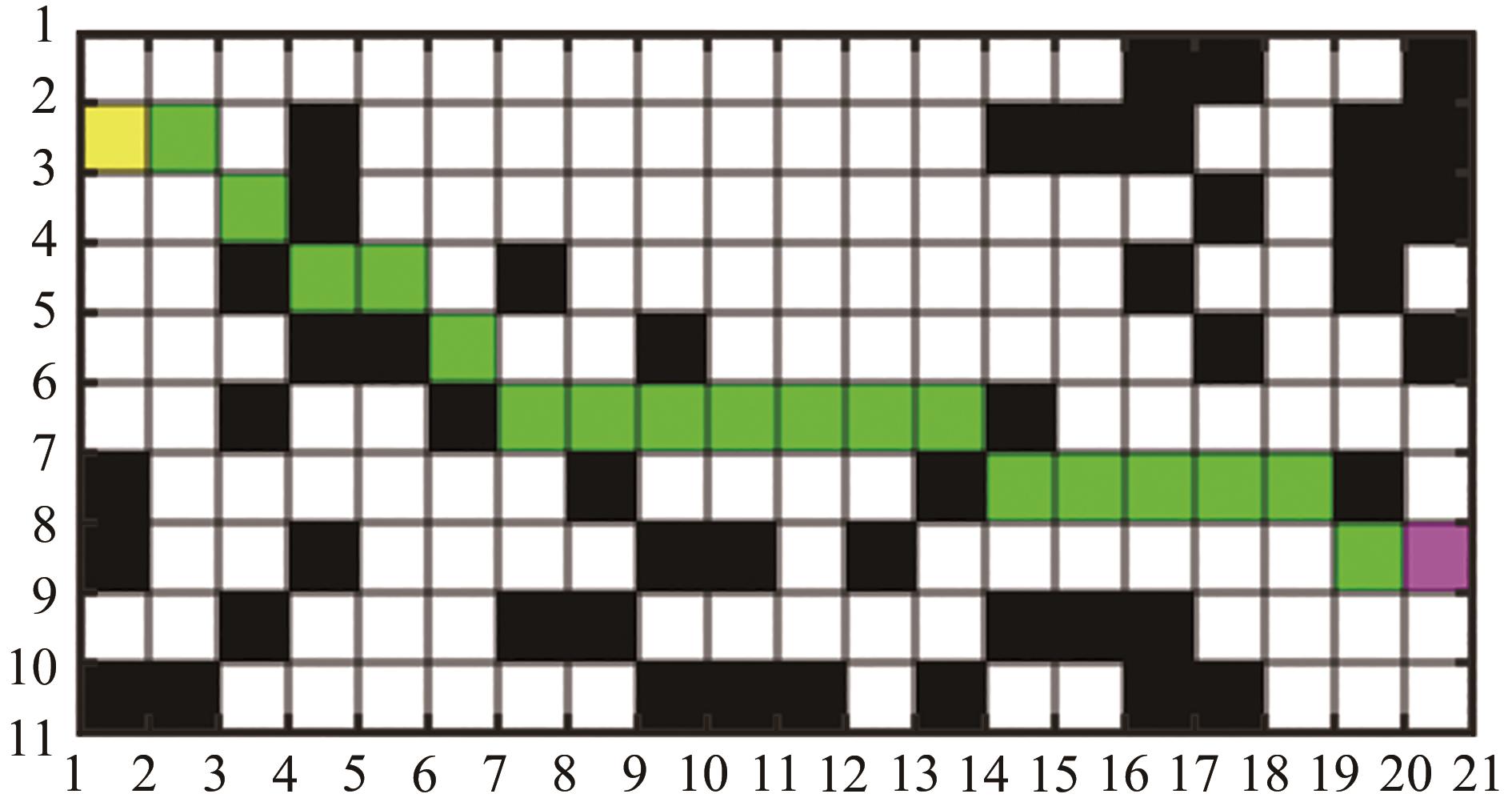
图9 LPA*算法仿真结果图

Fig. 9 Simulation result of LPA* algorithm

3 实验验证

3.1　仿真实验验证

为验证导向辊生产车间AGV的路径规划算法的有效性，给道路2边设置围挡，以此来提示机器人是否到达障碍边界，将导向辊生产车间模型优化如图10所示，便于进行路径规划。

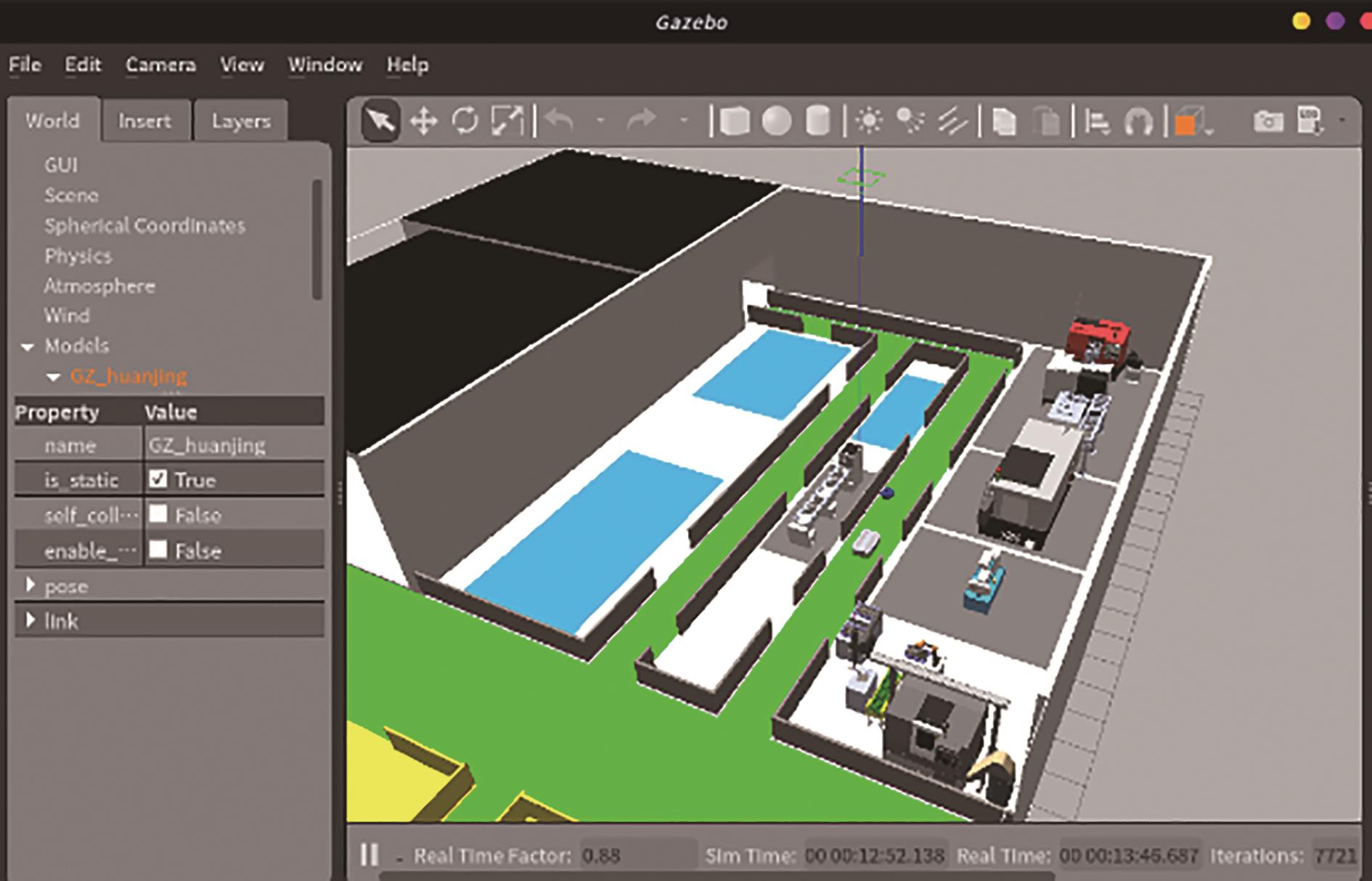
图10 优化后的车间模型图

Fig. 10 Model of optimized workshop

仿真所用的计算机性能参数为：Inter(R) Core(TM) i7-13700H，频率2.40 Hz，内存为16 G，六核CPU，运行系统为Ubuntu18.04，利用Robo Ware Studio软件对DWA和LPA*算法进行仿真，通过对起始点和目标点的输入实现算法的路径规划。

3.1.1　局部路径规划仿真实验验证

DWA算法属于局部路径规划算法，集成在路径规划器move_base中，通过RVIZ可视化窗口可以观察到局部路径规划的结果，如图11所示。

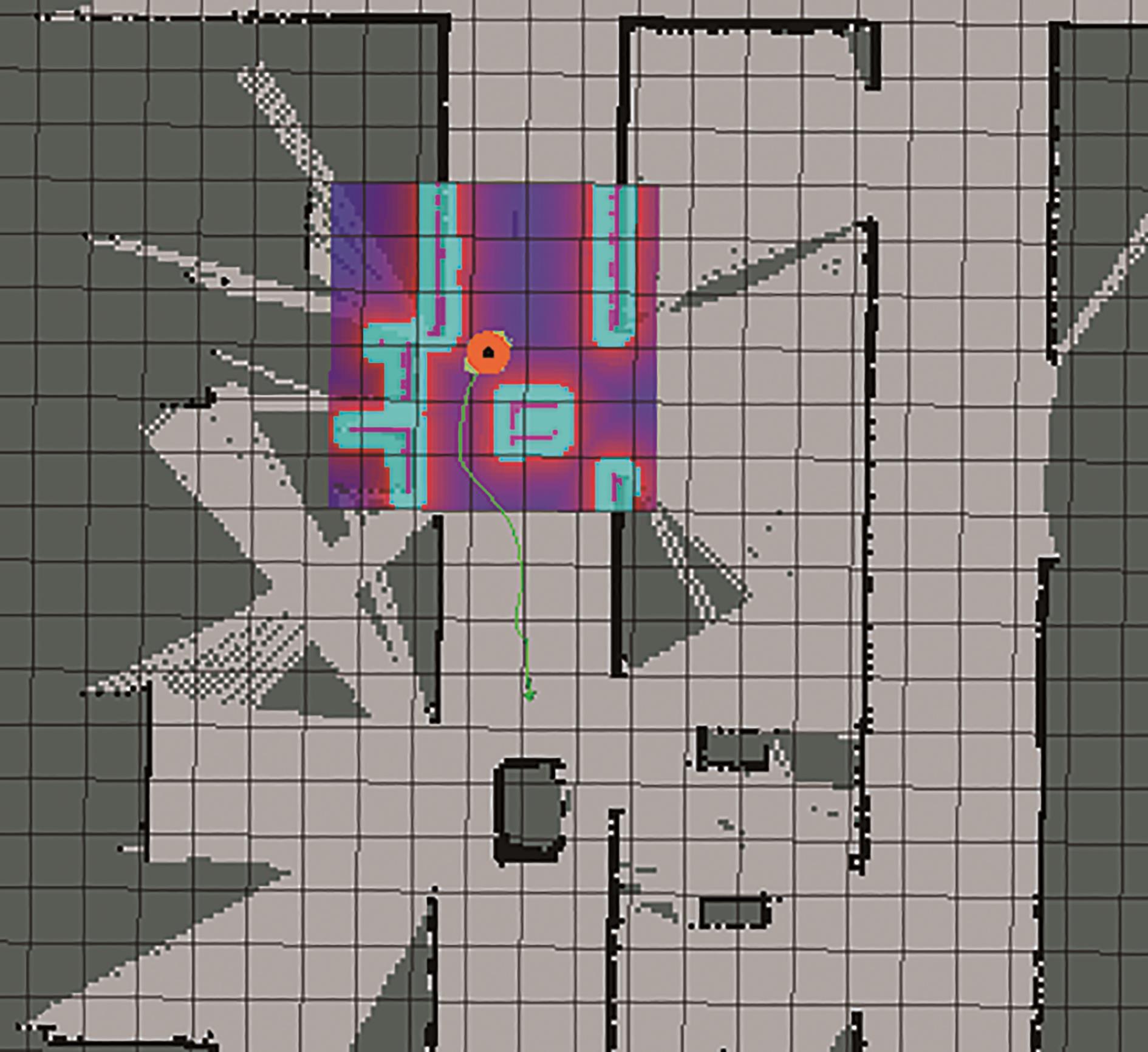
图11 局部路径规划

Fig. 11 Local path planning

图12为躲避出现的障碍物图。如图12(a)和图12(c)所示，道路中设置了长期障碍物和临时障碍物。由图12(b)可知，建立模型时设置一个长期障碍物，在设置目标点进行路径规划时就可直接避开这一障碍物；由图12(d)可知，在仿真空间中加入临时箱子障碍物时，在设置目标点进行路径规划的过程中会实时更新地图，显示出临时障碍物并进行局部路径的规划，从而绕过临时障碍物完成避障。

图12 躲避出现的障碍物

Fig. 12 Avoiding obstacles

3.1.2　全局路径规划仿真实验验证

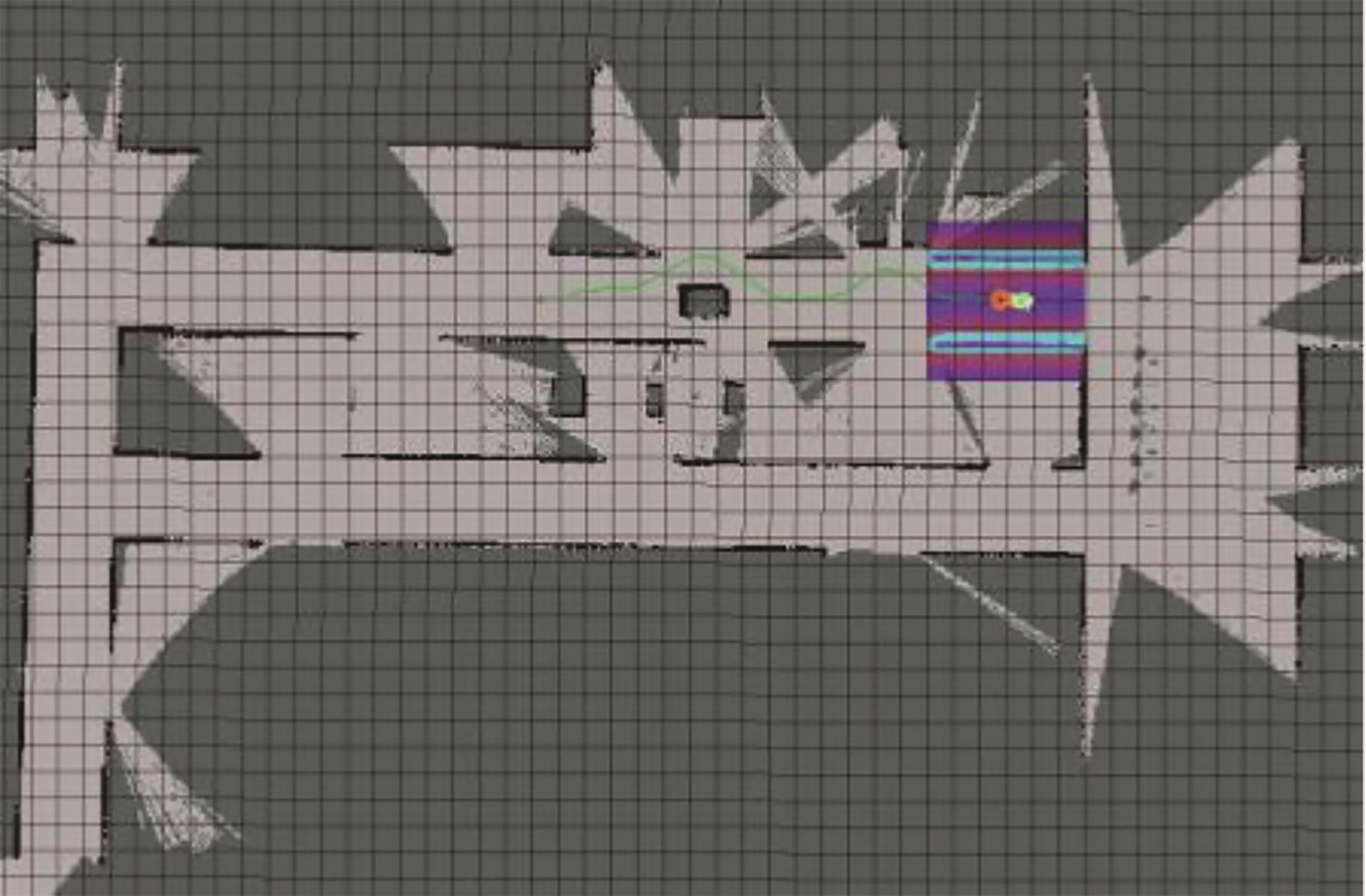
在全局路径规划中，将提前构建好的地图保存为pgm和yaml格式，并把文件存入maps文件夹，对yaml文件参数进行编辑，确定机器人在地图中的坐标位置。运行RVIZ显示地图，给定起始点和目标点，对整个导向辊生产车间进行全局路径规划，见图13。如图13所示，全局路径规划算法只能对已知障碍物进行避障规划，无法对出现的实时动态障碍物进行避障处理。

图13 全局路径规划

Fig. 13 Global path planning

3.1.3　组合路径规划仿真实验验证

针对导向辊生产车间环境多变的问题，采用融合LPA*算法与DWA算法的组合路径规划方法，解决导向辊生产车间AGV避障与路径规划问题。当明确AGV的初始位姿和目标点，就能规划出一条最优的全局路径，当AGV遇到动态障碍物没有到达目标点时进行局部路径规划，做到及时避障，整体流程图如图14所示。

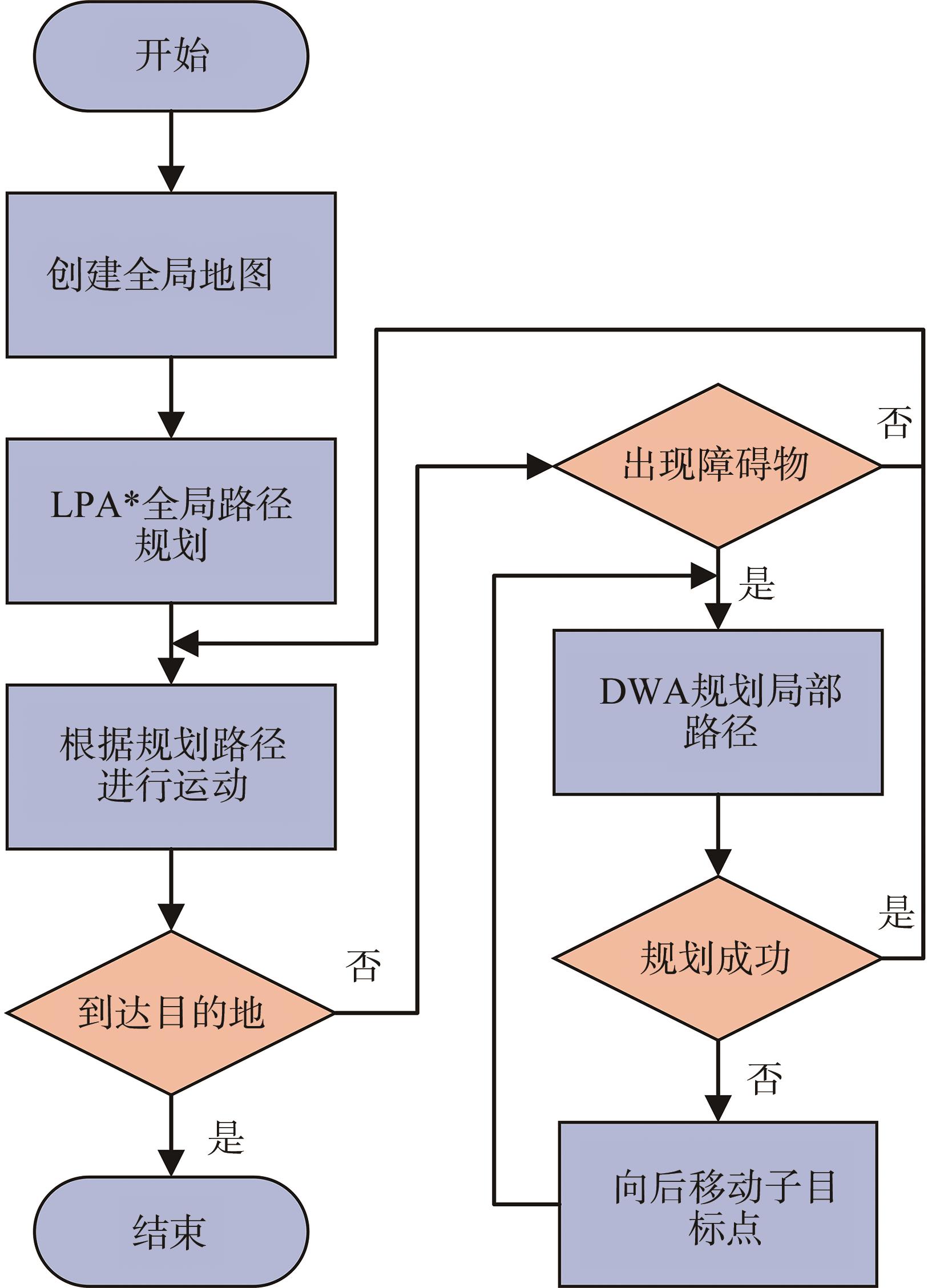
图14 组合路径规划流程图

Fig.14 Process diagram of combinatorial path planning

构建导向辊生产车间的仿真环境和二维栅格地图，并基于此进行组合路径规划的实验，如图15所示。

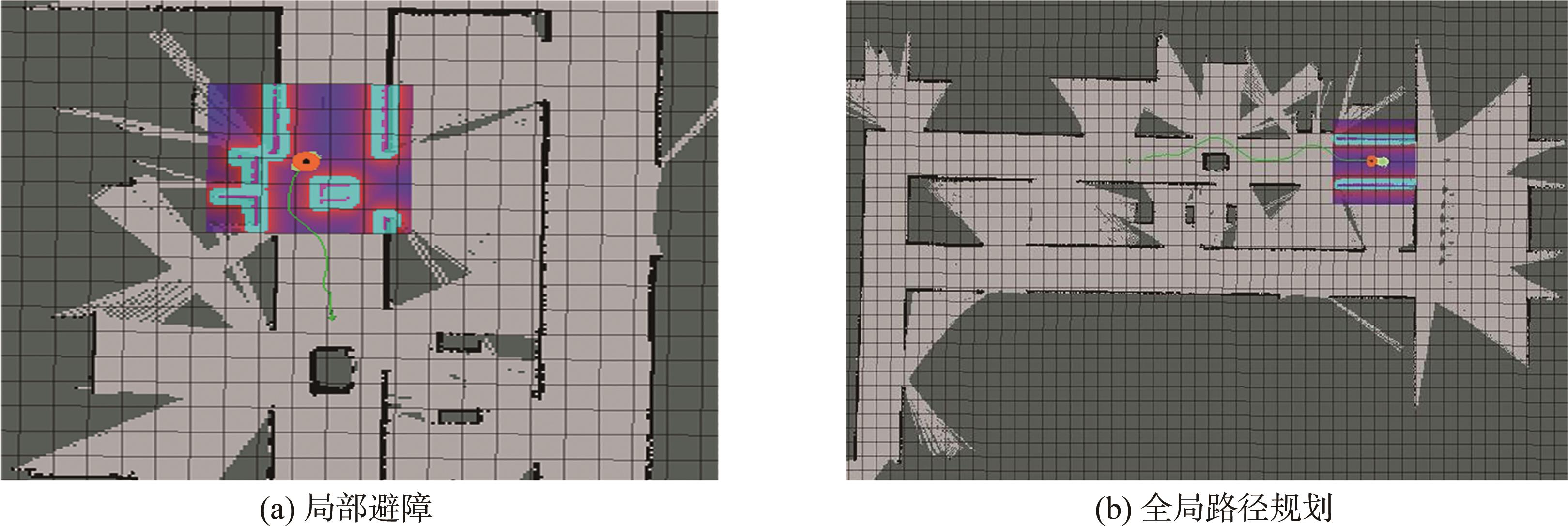
图15 组合路径规划

Fig. 15 Combined path planning

在制造导向辊的二维栅格地图中，设定一个目标点并使用LPA*算法计算出最优的全局路径，在AGV运动的过程中加入临时障碍物，局部路径规划任务通过绕过障碍物完成避障，最终AGV成功到达设置的目标点。

3.2　实地场景验证

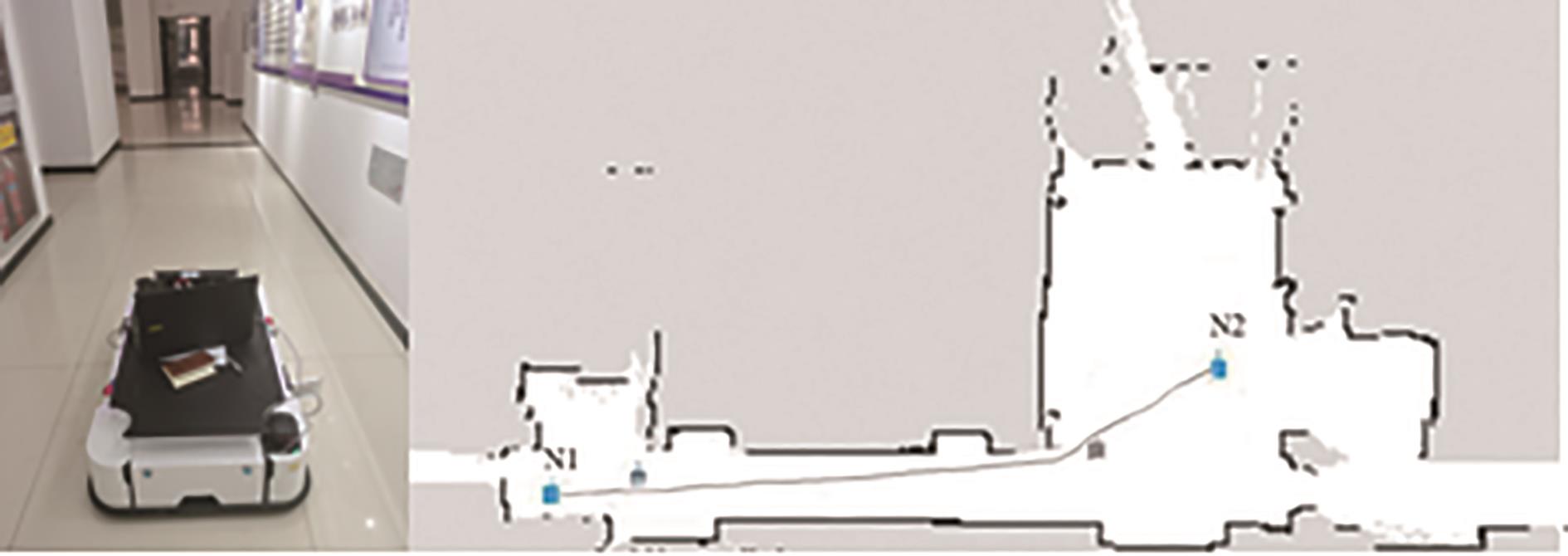
实验场景为综合楼一楼实验室外的一段楼道，见图16。如图16所示，N1为起始位置，N2为目标位置，分别用A*算法、LPA*算法和组合算法进行路径规划。

图16 组合路径规划示意图

Fig. 16 Schematic diagram of combined path planning

路径规划实验结果如表1所示。由表1可知，A*算法的路径规划时间最久，组合路径规划方法所用时间最短。传统的A*算法在实验场景出现障碍物时，会对整个地图重新进行路径计算，但障碍物的改变并不会影响之前求得的最短规划路径，从而导致路径规划时间最久。LPA*算法可以有效地减少地图的遍历次数，从而大大缩短规划时间，可以有效地解决动态环境下从给定起点到给定目标点的最短路径问题，但其只能对已知障碍物进行避障规划，无法对出现的实时动态障碍物进行避障处理。而组合路径规划算法融合了LPA*算法和DWA算法的优点，若已知AGV的初始位姿和目标点，就可规划出一条最优的全局路径，当AGV遇到动态障碍物而没有到达目标点时，将进行局部路径规划，做到及时避障。

表1 路径规划结果

Table 1 Path planning results

路径规划算法	路径长度/m	规划时间/s
A*算法	35.4	10.58
LPA*算法	36.2	4.23
组合路径规划算法	36.0	1.99

从实验结果可以看出，组合路径规划算法与传统A*算法和LPA*算法相比，均表现出了明显的性能优势。在路径长度方面，组合路径规化算法相较于传统A*算法增加了1.7%，相较于LPA*算法减少了0.6%。路径长度变化不明显，是由于组合路径算法对动态障碍物有冲突预判距离，当遇到动态未知障碍物时，可以避开动态障碍物。在规划时间方面，该算法相较于传统A*算法和LPA*算法分别减少了81.2%和52.9%。本研究提出的组合路径规化算法可以有效地完成移动机器人的路径规划，并且寻路时间更短，极大地提升了路径规划的效率。

4 结论

本研究以造纸类机械导向辊生产车间物料运输机器人为研究对象，以车间生产导向辊工艺流程为基础，针对导向辊生产车间各工位间的物料运输问题，首先建立了自动引导车（Automated Guided Vehicle，AGV）运动模型与导向辊生产车间模型；之后提出了局部与全局组合的路径规划算法，采用LPA*算法进行全局路径规划，采用DWA算法进行局部路径规划，可有效解决AGV紧急避障和最优路径选取等问题，提高寻路算法的效率；最后针对构建的导向辊生产车间模型将提出的组合路径规划算法进行实验验证。

组合路径规化算法的实验结果表明，相较于传统A*算法和LPA*算法，该算法的规划时间分别减少了81.2%和52.9%，大大降低路径规划的时间和计算量，解决了AGV工作过程中的实时避障和路径规划时间长等问题，验证了组合算法的可靠性与实用性，极大地提升了规划的效率。

参考文献

魏文光，黄鹏，王胜丹，等. 造纸企业智能仓储系统技术研究［J］. 中国造纸， 2023， 42（10）： 149-154. [百度学术]

WEI W G， HUANG P， WANG S D， et al. Research on Intelligent Warehousing System Technology for Papermaking Enterprises［J］. China Pulp & Paper， 2023， 42（10）： 149-154. [百度学术]

罗喜，张成峰，邱杰. 基于人工智能的安全预警装置在纸卷仓储的应用［J］. 中国造纸， 2023， 42（9）： 145-147. [百度学术]

LUO X， ZHANG C F， QIU J. Application of AI-based Security Warning Device in Paper Roll Warehousing［J］. China Pulp & Paper， 2023， 42（9）： 145-147. [百度学术]

任永杰，赵显，郭思阳，等. 基于wMPS和模糊控制的AGV路径规划控制［J］. 光学学报， 2019， 39（3）： 191-198. [百度学术]

REN Y J， ZHAO X， GUO S Y， et al. AGV Path Planning and Control Based on wMPS and Fuzzy Control［J］. Acta Optica Sinica， 2019， 39（3）： 191-198. [百度学术]

朱大奇，颜明重. 移动机器人路径规划技术综述［J］. 控制与决策， 2010， 25（7）： 961-967． [百度学术]

ZHU D Q， YAN M Z. Overview of Mobile Robot Path Planning Techniques［J］. Control and Decision， 2010， 25（7）： 961-967. [百度学术]

LIMA D G， JOHN G. Fixed Points of N-valued Maps on Surfaces and the Wecken Property—A Configuration Space Approach［J］. Science China（Mathematics）， 2017， 60（9）： 1561-1574. [百度学术]

JUNG I K， HONG K B， HONG S K， et al. Path Planning of Mobile Robot Using Neural Network［C］//Proceedings of the IEEE International Symposium on Industrial Electronics. Sloveniai： IEEE， 1999. [百度学术]

祝继华，周颐，王晓春，等. 基于图像配准的栅格地图拼接方法［J］. 自动化学报， 2015， 41（2）： 285-294. [百度学术]

ZHU J H， ZHOU Y， WANG X C， et al. Grid Map Stitching Method Based on Image Registration［J］. Acta Automatica Sinica， 2015， 41（2）： 285-294. [百度学术]

VADAKKEPAT P. Evolutionary Artificial Potential Fields and Their Application in Real Time Robot Path Planning［C］//Proceedings of the 2000 Congress on Evolutionary Computation. LaJolla： IEEE， 2002： 256-263. [百度学术]

ZHANG Q R， GU G C. Path Planning Based on Improved Binary Particle Swarm Optimization Algorithm［C］//2008 IEEE Conference on Robotics， Automation & Mechatronics. Chengdu： IEEE， 2008： 462-466. [百度学术]

HART P E， NILSSON N J， RAPHAEL B. A Formal Basis for the Heuristic Determination of Minimum Cost Paths［J］. IEEE Transactions on Systems Science & Cybernetics， 1972， 4（2）： 28-29. [百度学术]

DIJKSTRA E W. A Note on Two Problems in Connexion with Graphs［J］. Numerische Mathematik， 1959， 1（1）： 269-271. [百度学术]

STENTZ A. Optimal and Efficient Path Planning for Partially-known Environments［C］//Proceedings of the 1994 IEEE International Conference on Robotics and Automation. San Diego： IEEE， 1994： 3310-3317. [百度学术]

KOENIG S， LIKHACHEV M. Fast replanning for navigation in unknown terrain［J］. IEEE Transactions on Robotics， 2005， 21（3）： 354-363. [百度学术]

HARABOR D D， GRASTIEN A. Online Graph Pruning for Pathfinding on Grid Maps［C］//25th AAAI Conference on Artificial Intelligence. San Francesco：Aaai Conference on Artificial Intelligence. 2011： 1114-1119. [百度学术]

YANG Y， LI J T， PENG L L. Multi-robot Path Planning Based on a Deep Reinforcement Learning DQN Algorithm［J］. CAAI Transactions on Intelligence Technology， 2020， 5（3）： 177-183. [百度学术]

黄程侃. 基于视觉的激光SLAM AGV初定位与路径规划研究［D］. 杭州：浙江工业大学， 2020. [百度学术]

HUANG C K. Research on Initial Positioning and Path Planning of Visual-based Laser SLAM AGV［D］. Hangzhou： Zhejiang University of Technology， 2020. [百度学术]

李生，李明宇，方舟，等. 基于改进LPA*算法的虚拟人路径规划［J］. 装备制造技术， 2022（8）： 82-84. [百度学术]

LI S， LI M Y， FANG Z， et al. Virtual Human Path Planning Based on Improved LPA* Algorithm［J］. Equipment Manufacturing Technology， 2022（8）： 82-84. [百度学术]

ZHANG L Y， HAN Y， JIANG B. Research on Path Planning Method of Unmanned Boat Based on Improved Artificial Potential Field Method［J］. 2022 6th Asion Conference on Artificial Intelligence Technology （ACAIT）. Chengdu： IEEE. 2022： 1-10. CPP [百度学术]

（责任编辑：吕子露） [百度学术]

融合LPA*和DWA算法的导向辊生产车间AGV组合路径规划方法研究

摘要

关键词

1 导向辊生产线车间建模

1.1 AGV运动模型

1.2 导向辊生产车间模型构建

2 导向辊生产线车间AGV路径规划方法

2.1 局部路径规划算法设计

2.2 全局路径规划算法设计