摘要
本文总结了计算机模拟技术在纤维形态模拟中的应用研究进展,并在此基础上分析了多种纤维材料的可视化技术及性能预测与对比,以期为实现纤维在材料中的定位模拟研究和功能材料的开发提供思考。
纤维包括天然纤维和合成纤
由纤维和孔隙组成的多孔纤维材料物理及光学等性能易受纤维本身的性质及孔隙结构影
计算机模拟技术主要是通过几种计算机模拟软件来进行实现的,目前主流使用并应用于多孔材料的计算机模拟软件有Avizo、OpenGL和ANSY
在多孔纤维材料的研究中,Avizo是一种常用的模拟软件工具,可实现图像处理和三维可视化。通过扫描电子显微镜获得包含纤维网络材料的微观结构信息,将其导入至Avizo软件中进行二值化分割,以使纤维和背景分离出来,形成二值化图像,纤维部分为白色,背景部分为黑色,从而可准确提取纤维网络的形态特征。Avizo也可将二值化图像进行三维可视化处理。因此,基于二维图像结构特征参数进行三维模型重构的研究多使用Avizo进行。在Avizo中,通过调整视角、光照和颜色等参数,可观察和分析纤维网络的结构和特性,以了解纤维的连接方式、孔隙分布和纤维间距等信息。对于与纤维材料整体孔隙结构参数相关的性能(如透气性、渗透率等)来说,有着完整重建孔隙结构模块的Avizo更适用于这类研究。
OpenGL是一种图形编程接口,可利用数学模型和坐标点数据来描述纤维的几何形状,以及其在多孔材料中的排列方式,可以使用数学模型和坐标点数据来捕捉纤维的长度、宽度、高度等几何属性,从而更详细地了解纤维的几何特征。也就是说,OpenGL可以胜任从纤维模型开始的纯模拟模型,其建立的纤维几何模型能够定量地分析纤维在多孔材料中的分布和排列。使用OpenGL进行可视化处理,将建模得到的纤维堆积成纸张纤维的三维模型。通过调整渲染参数,如光照、材质和纹理,可以呈现出纤维材料的真实外观和质感。通过改变纤维的参数,如长度、宽度、取向等,来探索不同纤维排列对纸张性能的影响。此外,OpenGL还可以与其他模拟和分析工具结合使用,进一步研究纤维网络的力学行为、孔隙率等关键特性。对抗张强度、撕裂度等性能或以单根纤维为研究对象时,OpenGL则可以发挥其优势。
Aslannejad
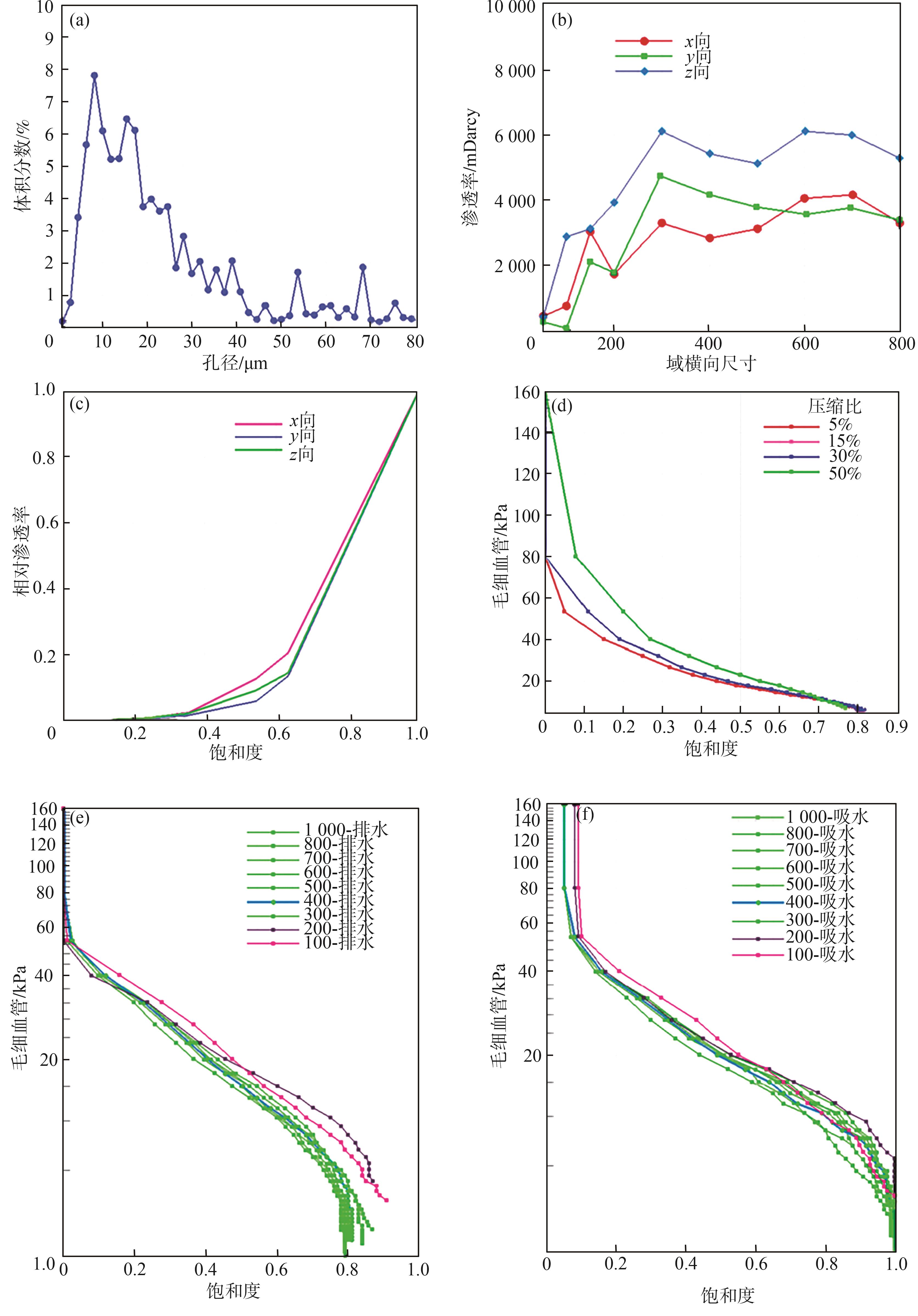
图1 (a)未涂布原纸的孔隙分布;(b)10个不同领域尺寸(x,y;其中x = y,且厚度为150 μm对于所有领域均恒定)的渗透率;(c)基于浸润相分布的相对渗透率曲线;(d)纸张变形对初次浸润曲线的影响; (e)所选域尺寸的排水曲线;(f)所选域尺寸的吸水曲
Fig. 1 (a) Porosity size distribution of the fiber layer, (b) permeability values for 10 different domain sizes (x, y; where x = y, and the thickness was constant at 150 μm for all domains), (c) relative permeability curve based on the distribution of the infiltrating phase, (d) drainage curve for the selected domain size, (e) capillary absorption curve for the selected domain size, (f) influence of paper deformation on the initial infiltration curv
Sen
Afrookhteh

图2 碳纸SEM
Fig. 2 SEM image of carbon pape
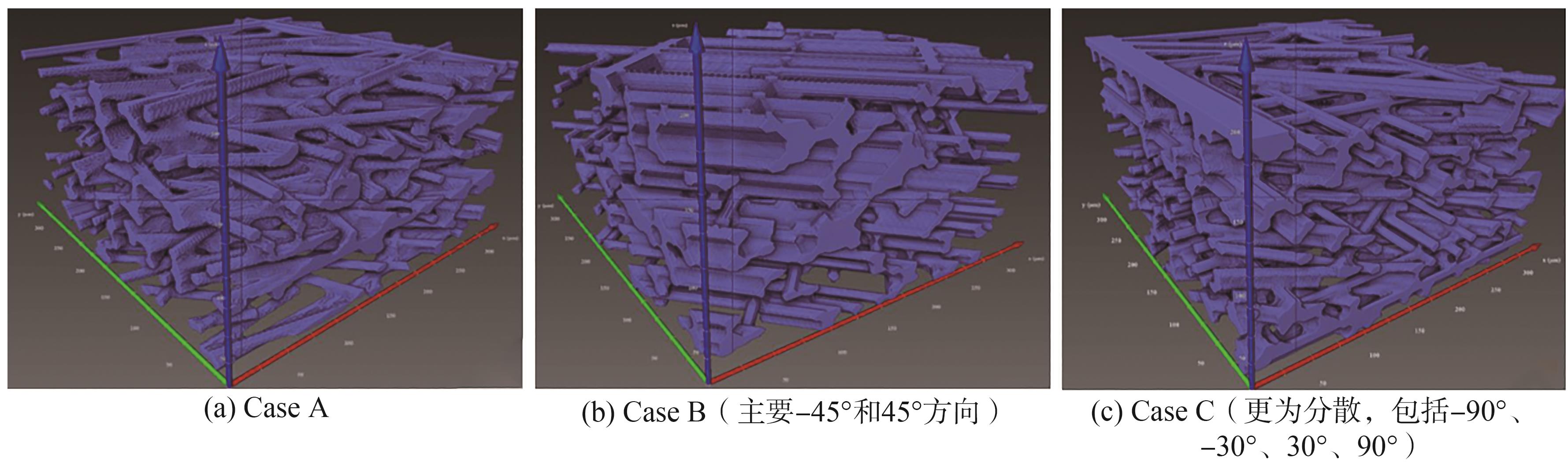
图3 碳纸的3种不同重建模
Fig. 3 Three different reconstruction model
注 浅蓝色为固相(纤维+黏结剂), 孔相透明。
Simaafrookhteh
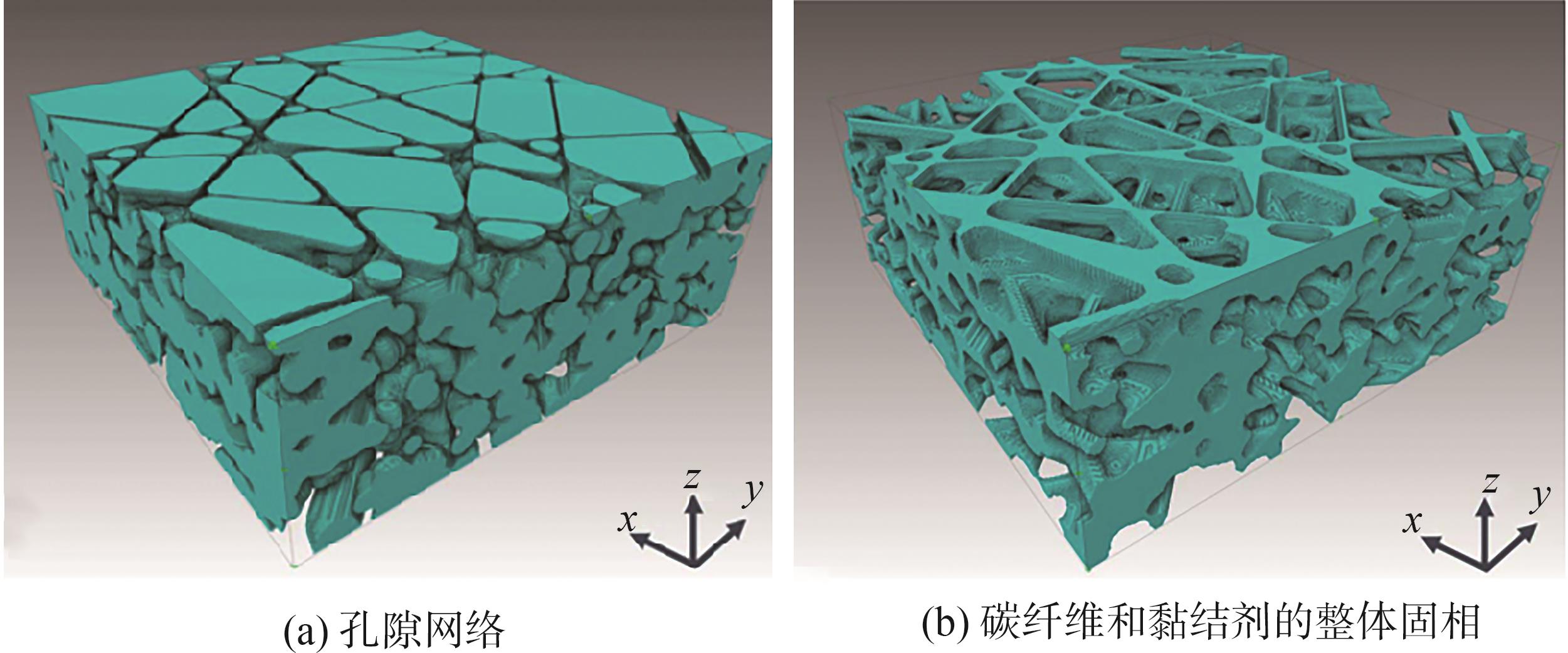
图4 碳纸的三维重构模
Fig. 4 Three-dimensional reconstruction model of carbon pape
Blanc
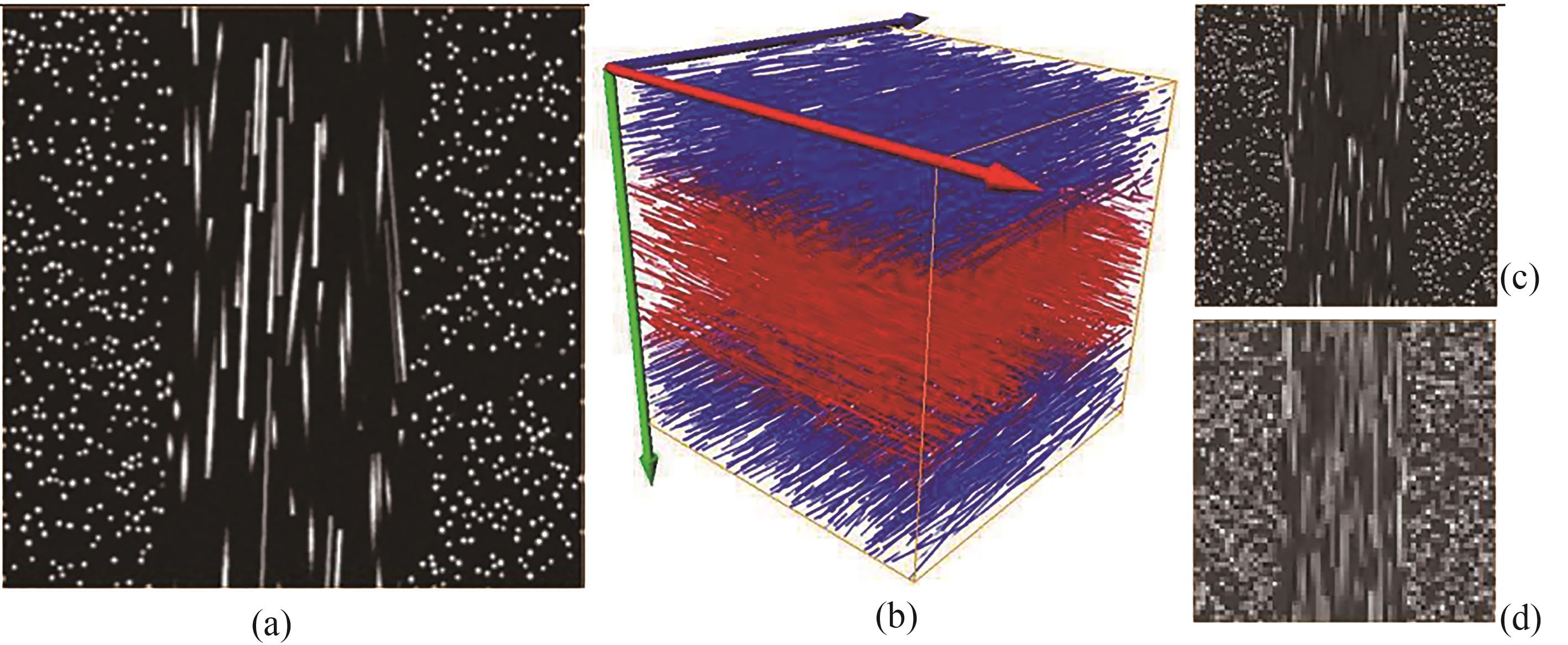
图5 纤维三维重建过
Fig. 5 Fiber three-dimensional reconstruction proces
注 (a)切片; (b)三维体渲染; (c)下采样系数为4; (d)下采样系数为8。
纤维基材料中,纤维间的交织与重叠成为其形成强度的主要来源。在纸张纤维的常规模拟中,常会出现纸张中的纤维在三维空间中相交、重叠或交织在一起的现象,即纤维交叉问题,其会在模拟过程中对纤维的有效长度、纤维之间的接触面积和纸张的孔隙结构造成影响,如
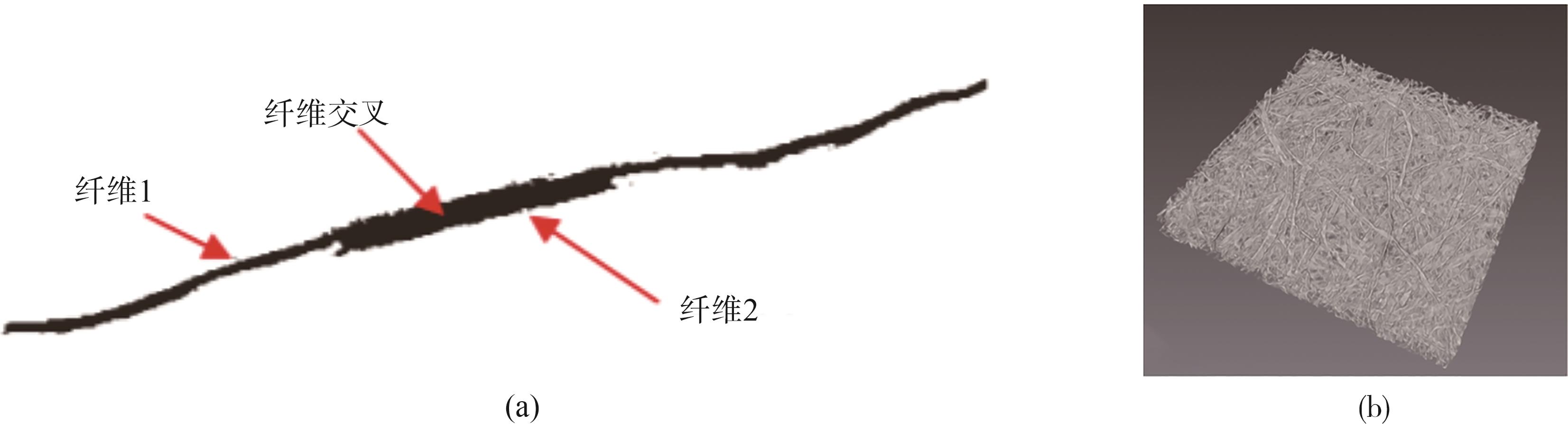
图6 (a) 二值化后纤维交叉示意图;(b)金属纤维纸张三维重建模型(1 mm×1 mm
Fig. 6 (a) Three-dimensional reconstruction model of metallic fiber paper (1 mm×1 mm), (b) schematic diagram of fiber intersections after binarization
Westenberge
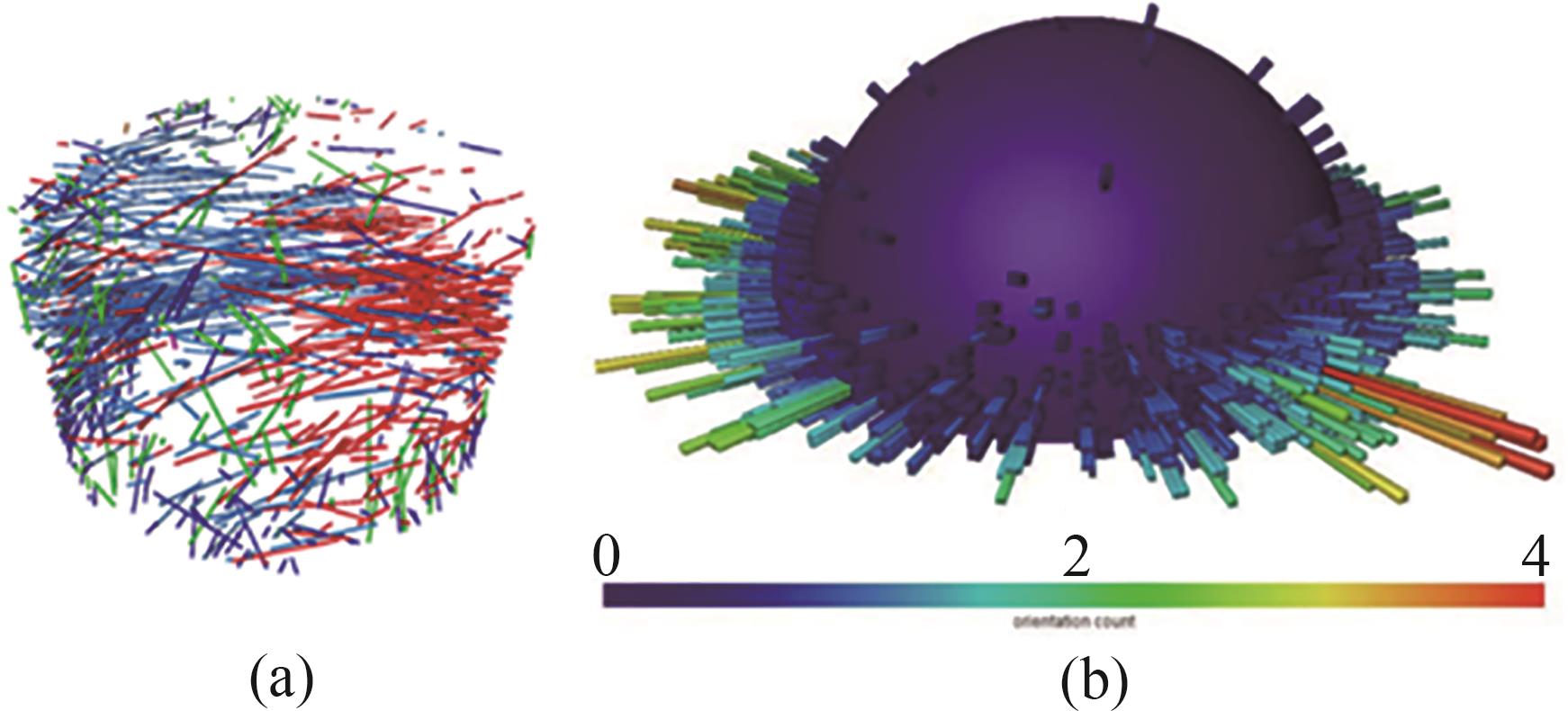
图7 (a) 不同颜色代表不同纤维取向的Avizo三维重建模拟图;(b) 超高性能纤维增强混凝土三维模拟图球状投
Fig. 7 (a) Avizo three-dimensional reconstruction simulation diagram with different colors representing different fiber orientations, (b) spherical projection of ultra-high performance fiber reinforced concrete three-dimensional simulation diagra
立方体模型是Conceição
| | | (1) |
其中,和是指2个最近的相邻单元格和,是任意单元格厚度的正整数。

图8 (a)立方体模型中的纤维表示方法;(b)基于立方体模型的三维结构模
Fig. 8 (a) Representation of fibers in a cubic model, (b) three-dimensional structural model based on the cubic mode
这些小立方体代表空间,且当某块空间被纤维模型占据时,则将立方体以黑色标注;被其他纤维或填充物占据时,以“X”标注;空白的立方体则是代表空闲区域。通过这种方法,不断将小立方体添加对应的标注,则可以得到三维结构模型图,如
Switzer
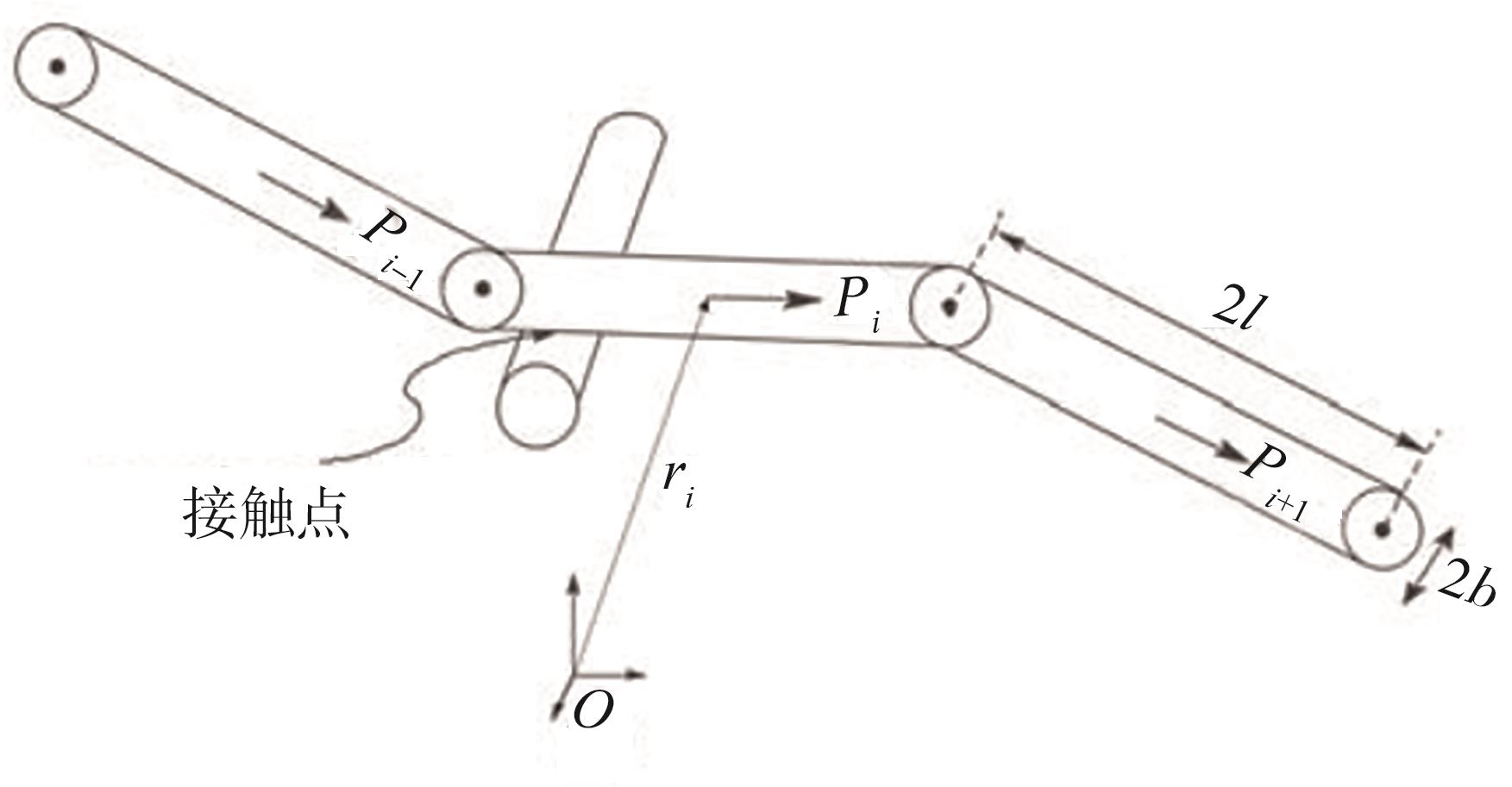
图9 球-棒模
Fig. 9 Schematic diagram of a model linked by ball and socket joint
为了进一步提高模型的精确度,Lavrykov
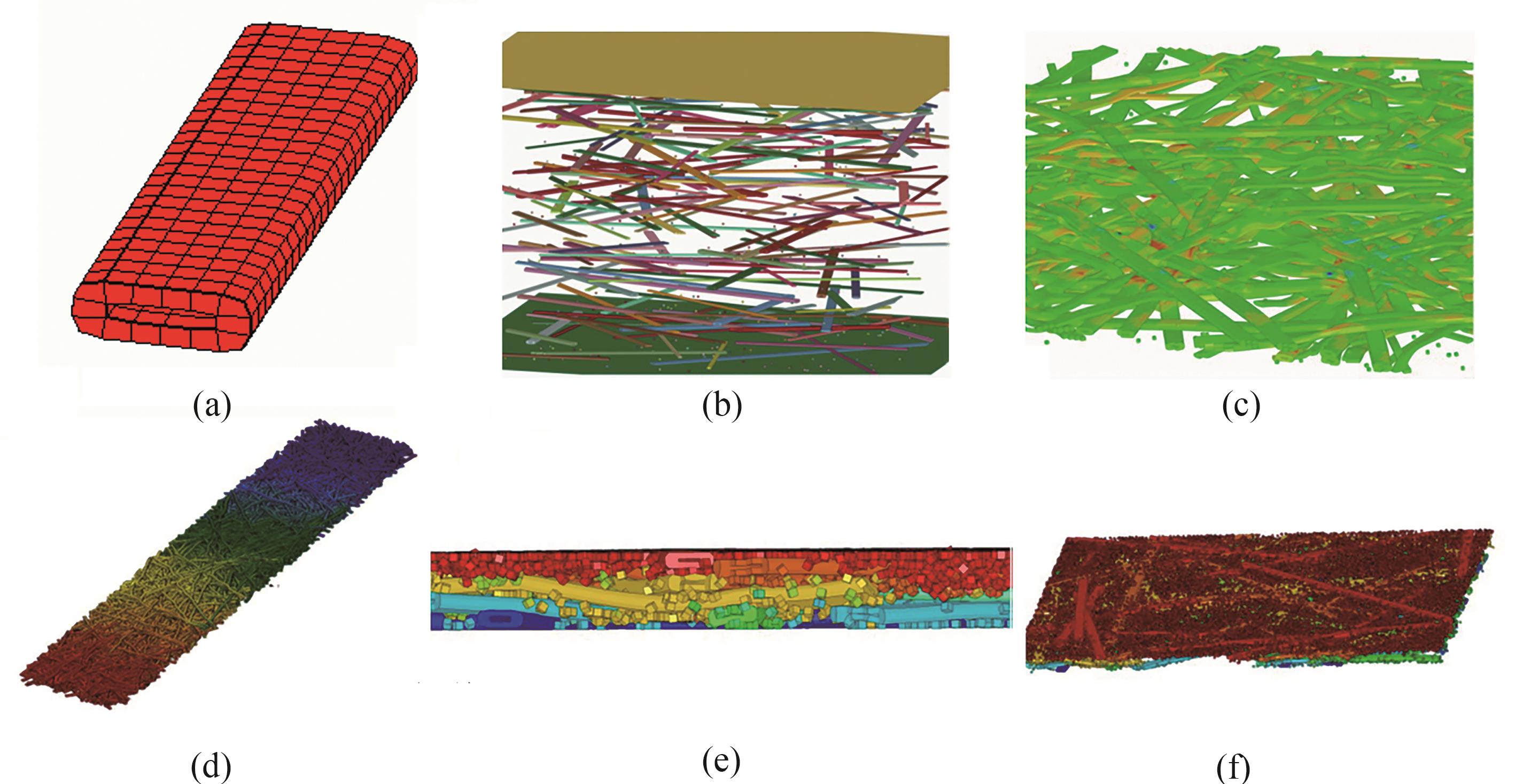
图10 (a) 有限元纤维模型;(b)纤维网络的初始配置示例(展示了所有4种纤维配置和填料颗粒);(c) 图(b)中经过压缩后的纤维网络;(d) 由50%针叶木和50%阔叶木浆纤维混合的样本;(e) 高填料含量的纤维网络的模拟示例;(f)在涂层形成过程中纤维层中填料颗粒的分布示
Fig. 10 (a) Finite element fiber model, (b) an example of initial configuration of fiber network (all four fiber configurations and filler particles are presented), (c) fiber network from Fig. (b) after compression, (d) the sample with 50% mixture of softwood and hardwood pulps, (e) fiber network with high filler content— an example of coating simulation, (f) filler particles distribution in the fiber mat during coating formation
纺织复合纤维材料的领域中,Melenka
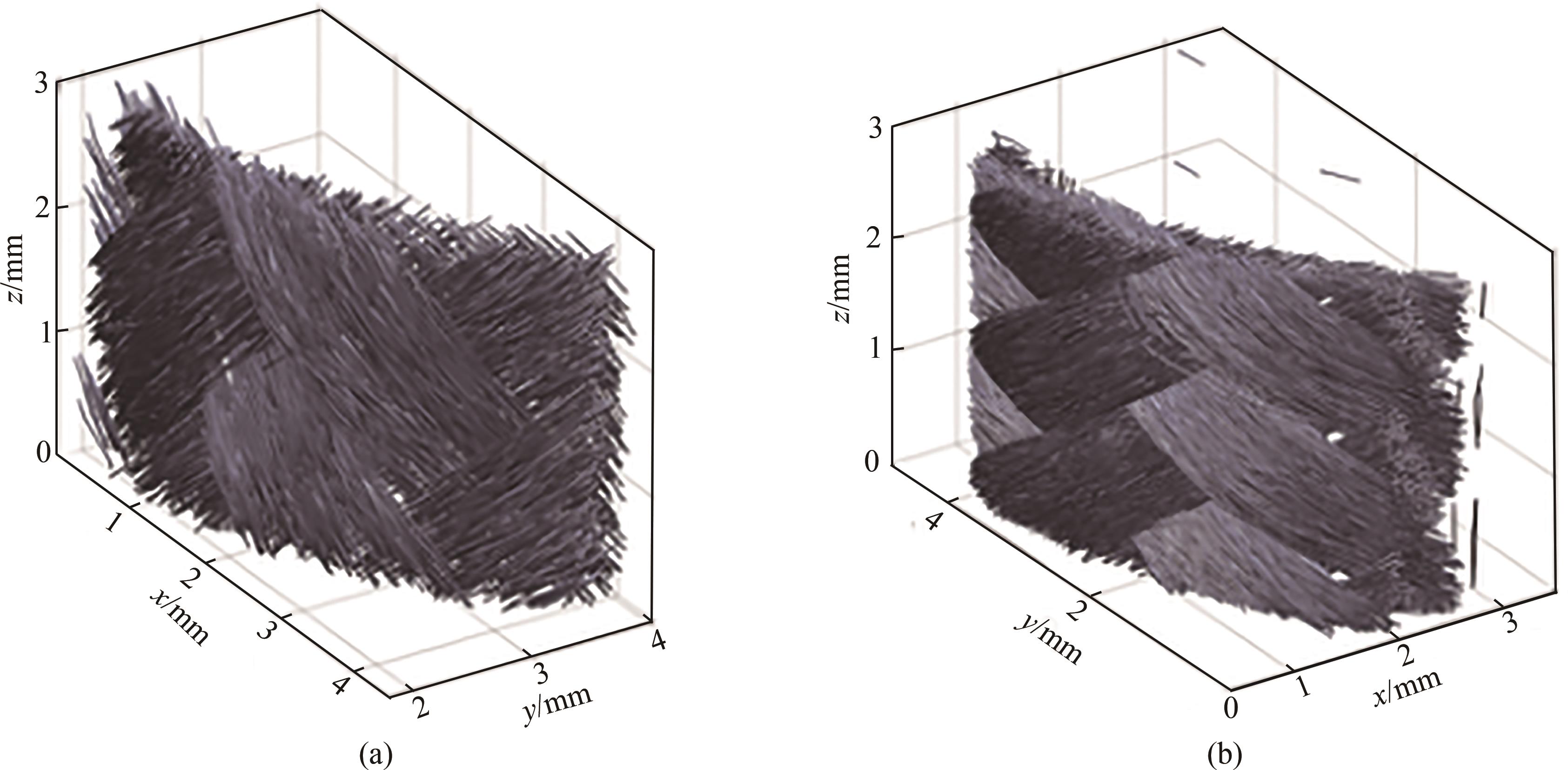
图11 利用纤维路径数据建立编织样的有限元分析网
Fig. 11 Establishing finite element analysis meshes for woven samples using fiber path dat
注 (a)样本1,具有45°的名义编织角;(b)样本2,具有55°的名义编织角。
质点弹簧模型是一种利用质点和弹簧模型取代目标物体原本结构,从而降低模拟复杂度的模拟方
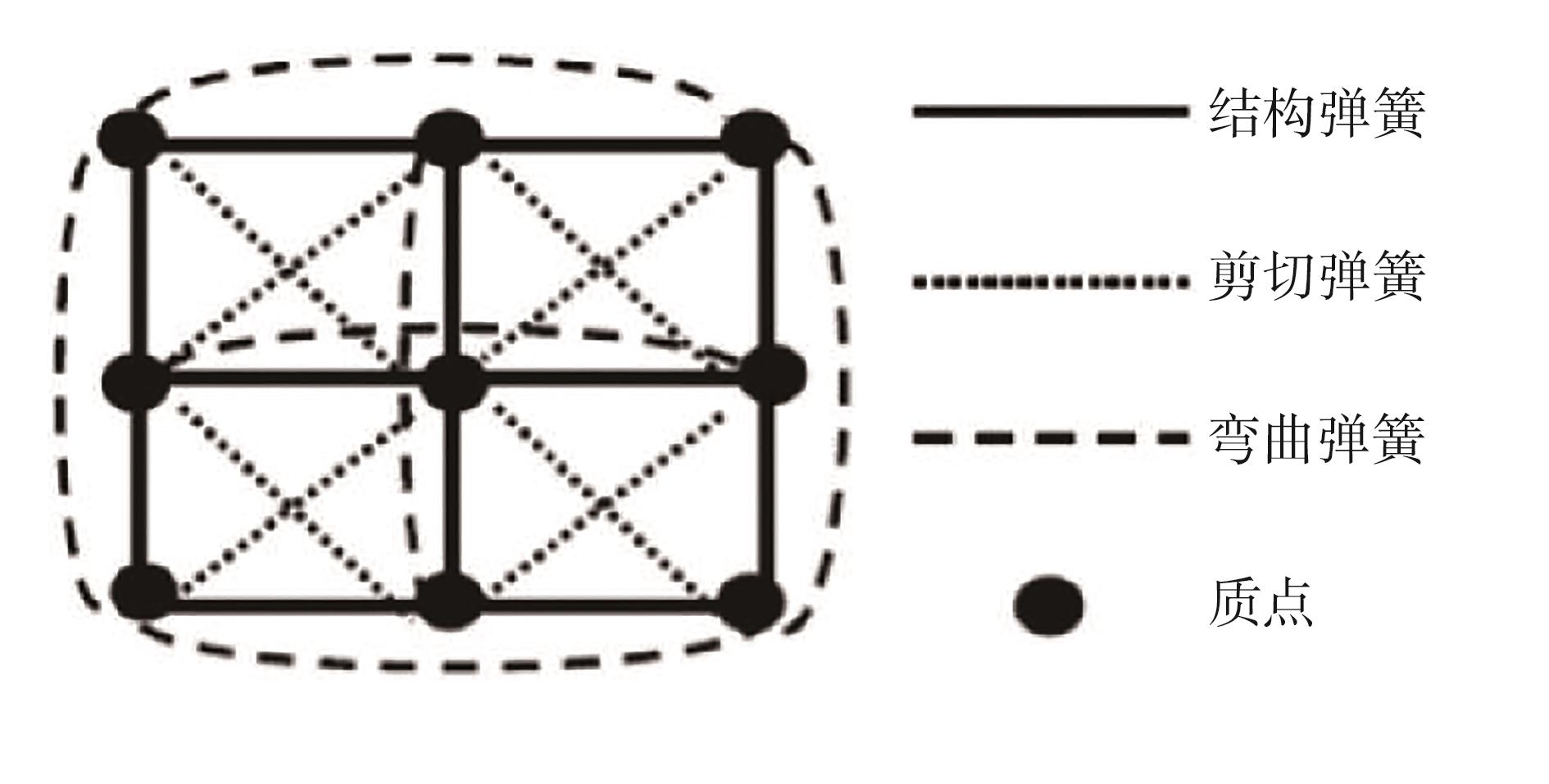
图12 质点-弹簧模型示意
Fig. 12 Schematic diagram of mass-spring mode
刘
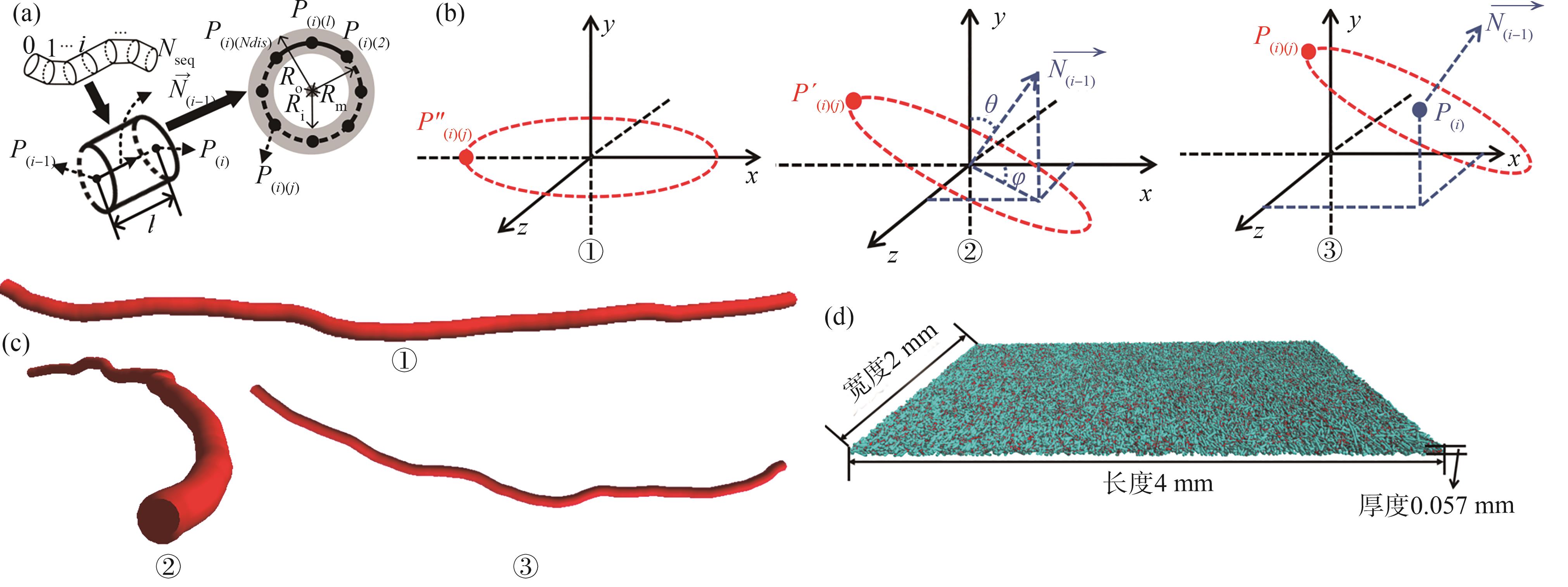
图13 离散化纤维模型使用OpenGL实现可视化
Fig. 13 Visualization of the discretized fiber model implemented using OpenGL
注 (a)植物纤维静态几何模型构造图;(b)纤维模型截面离散点坐标计算方法示意图;(c)植物纤维3D 模型在OpenGL 中的三视图;(d)3D 纸张结构模型示意图
三维梁沉积堆叠模型是由Motamedian

图14 三维梁沉积堆叠模型,不同的纤维网络中新纤维沉积的步
Fig. 14 Three-dimensional beam deposition and stacking model, different steps of deposition of a new fiber in the networ
注 (a) 查找与先前沉积的纤维的交点; (b) 提升交点; (c) 平滑纤维。
本文探讨了纤维形态与材料性能之间的关系,介绍了建立纤维基三维立体模型的理论基础以及相关的计算机模拟软件工具。通过模拟和预测纤维材料的性能理解纤维形态与材料性能之间的关系,并为纤维基材料领域的工艺改进和优化提供科学依据。然而,由于纤维的交叉、重叠及卷曲等形态复杂性和多样性,纤维形态和材料性能间的构效关系仍无法精确表达。通过引入反向传播神经网络算法、图像滤波算法、角点检测算法等与图像匹配、三维重建和目标识别等相关的先进算法以提高计算精度,从而可能实现符合不同纤维特性的模拟与仿真;通过引入灰度共生矩阵、碰撞模型等克服孔洞不连贯、纤维层偏移等不良因素对模拟精度的阻碍,从而更好地明确纤维参数对复合材料性能的影响,并进一步扩大计算机模拟技术在纤维材料的实际应用范围。
参考文献
CHANDRAMOHAN D, MARIMUTHU K. A review on natural fibers [J]. International Journal of Research and Reviews in Applied Sciences, 2011, 8 (2):194-206. [百度学术]
WANG J, DAI Q, SI R, et al. Investigation of properties and performances of Polyvinyl Alcohol (PVA) fiber-reinforced rubber concrete [J]. Construction and Building Materials, 2018, 193:631-642. [百度学术]
DU X, XIN B, CHUN W, et al. Waterproof and moisture permeable nanofibrous membranes with multi-scale cross-linked structure [J]. Journal of Natural Fibers, 2022, 19 (13):5088-5100. [百度学术]
COSTA L R, SILVA L E, MATOS L C, et al. Cellulose nanofibrils as reinforcement in the process manufacture of paper handsheets [J]. Journal of Natural Fibers, 2022, 19 (14):7818-7833. [百度学术]
MILANOVIC J, LAZIC T, ZIVKOVIC I, et al. The effect of nanofibrillated tempo-oxidized cotton linters on the strength and optical properties of paper [J]. Journal of Natural Fibers, 2022, 19 (11):3993-4006. [百度学术]
MOURA M J, FERREIRA P, FIGUEIREDO M. Mercury intrusion porosimetry in pulp and paper technology [J]. Powder Technology, 2005, 160 (2):61-66. [百度学术]
AXELSSON M. Image analysis for volumetric characterisation of microstructure [M]. Uppsala: Centre for Image Analysis, Swedish University of Agricultural Sciences, 2009:9-77. [百度学术]
AXELSSON M, SVENSSON S. 3D pore structure characterisation of paper [J]. Pattern Analysis and Applications, 2010, 13:159-172. [百度学术]
DELERUE J, PERRIER E, YU Z, et al. New algorithms in 3D image analysis and their application to the measurement of a spatialized pore size distribution in soils [J]. Physics and Chemistry of the Earth, 1999, 24 (7):639-644. [百度学术]
HUANG S, GOEL A, RAMASWAMY S, et al. Transverse and in-plane pore structure characterisation of paper [J]. Appita Journal, 2002, 55 (3):230-234. [百度学术]
OSMANI S A. Variation of stresses at different nodal points in a isotropic beam using ANSYS [J]. American Journal of Engineering Research, 2015,5 (3):105-110. [百度学术]
ASLANNEJAD H, HASSANIZADEH S. Study of hydraulic properties of uncoated paper: Image analysis and pore-scale modeling [J]. Transport in Porous Media, 2017, 120:67-81. [百度学术]
SENG D W. Visualization of Composite Materials’ Microstructure with OpenGL [J]. Applied Mechanics and Materials, 2012, 189:478-481. [百度学术]
AFROOKHTEH S S, JAMALI J, SHAKERI M, et al. Stochastic reconstruction of carbon fiber paper gas diffusion layers of PEFCs: A comparative study [J]. Energy Equipment and Systems, 2018, 6 (1):51-59. [百度学术]
SIMAAFROOKHTEH S, TAHERIAN R, SHAKERI M. Stochastic microstructure reconstruction of a binder/carbon fiber/expanded graphite carbon fiber paper for PEMFCs applications: mass transport and conductivity properties [J]. Journal of the Electrochemical Society, 2019, 166 (7):3287-3299. [百度学术]
BLANC R, WESTENBERGER P. Comparison of fiber orientation analysis methods in Avizo[C]//Proceedings of the 7th Conference on Industrial Computed Tomography (iCT2018), Leuven: Research Group Computed Tomography, 2017:1-5. [百度学术]
BEZRUKOV A, STOYAN D. Simulation and statistical analysis of random packings of ellipsoids [J]. Particle & Particle Systems Characterization, 2006, 23 (5):388-398. [百度学术]
WOLFINGER T, WESTENBERGER P. Evaluation of specific network properties of paper using computer tomography and the latest Avizo fire analysing tools[C]//Proceedings of the 5th Conference on Industrial Computed Tomography (iCT 2014), Wels: Research Group Computed Tomography, 2014:97-102. [百度学术]
WESTENBERGER P, ESTRADE P, LICHAU D. Fiber orientation visualization with Avizo Fire®[C]//Proceedings of the Conference of Industrial Computed Tomography (iCT2012), Jounieh: Research Group Computed Tomography, 2012:99-104. [百度学术]
CONCEIÇÃO E L, CURTO J M, SIMõES R M, et al. Coding a simulation model of the 3D structure of paper[C]//Proceedings of the Computational Modeling of Objects Represented in Images: Second International Symposium, Buffalo: Springer, 2010: 299-310. [百度学术]
SWITZER L H, KLINGENBERG D J, TIM C. Handsheet formation and mechanical testing via fiber-level simulations [J]. Nordic Pulp & Paper Research Journal, 2004, 19 (4):434-439. [百度学术]
LAVRYKOV S, RAMARAO B, LINDSTRöM S, et al. 3D network simulations of paper structure [J]. Nordic Pulp & Paper Research Journal, 2012, 27 (2):256-263. [百度学术]
MELENKA G W, GHOLAMI A. Fiber identification of braided composites using micro-computed tomography [J]. Composites Communications, DOI:10.1016/J.COCO.2021.100813. [百度学术]
RIGORT A, GüNTHER D, HEGERL R, et al. Automated segmentation of electron tomograms for a quantitative description of actin filament networks [J]. Journal of Structural Biology, 2012, 177 (1):135-144. [百度学术]
WEBER B, GREENAN G, PROHASKA S, et al. Automated tracing of microtubules in electron tomograms of plastic embedded samples of Caenorhabditis elegans embryos [J]. Journal of Structural Biology, 2012, 178 (2):129-138. [百度学术]
BYUN J H . The analytical characterization of 2D braided textile composites [J]. Composites Science and Technology, 2000, 60 (5):705-716. [百度学术]
MELENKA G, PASTORE C, KO F, et al. Advances in 2D and 3D braided composite material modeling [J]. Handbook of Advances in Braided Composite Materials, DOI:10.1016/b978-0-08-100369-5.00009-x. [百度学术]
MOZAFARY V, PAYVANDY P. Study and comparison techniques in fabric simulation using mass spring model [J]. International Journal of Clothing Science and Technology, 2016, 28 (5):634-689. [百度学术]
HWANG S M, SONG B H, YUN H K. Fuzzy inference of textile animation based on Mass-Spring model[C]//Proceedings of the 16th North-East Asia Symposium on Nano, Information Technology and Reliability, Macao: IEEE, 2011: 130-135. [百度学术]
PROVOT X. Deformation constraints in a mass-spring model to describe rigid cloth behaviour[C]//Proceedings of the Graphics interface, Québec: Canadian Information Processing Society, 1995: 147-154. [百度学术]
刘 寅. 基于造纸纤维特性模型的纸页结构计算机模拟及性能预测方法研究 [D]. 广州:华南理工大学, 2020. [百度学术]
LIU Y. Methodology Study on the Paper Structure Simulation and Property Prediction Based on Paper Fiber Property Modeling [D]. Guangzhou:South China University of Technology,2020. [百度学术]
MOTAMEDIAN H R, KULACHENKO A. Simulating the hygroexpansion of paper using a 3D beam network model and concurrent multiscale approach [J]. International Journal of Solids and Structures, 2019, 161:23-41. [百度学术]
FEYNMAN C R. Modeling the appearance of cloth [D]. Boston: Massachusetts Institute of Technology, 1986. [百度学术]
TERZOPOULOS D, PLATT J, BARR A, et al. Elastically deformable models[C]// Proceedings of the the 14th annual conference on computer graphics and interactive techniques, Anaheim: Association for Computing Machinery, 1987: 205-214. [百度学术]
DAI X, LI Y, ZHANG X. Simulating anisotropic woven fabric deformation with a new particle model [J]. Textile Research Journal, 2003, 73 (12):1091-1099. [百度学术]
EBERHARDT B, WEBER A, STRASSER W. A fast, flexible, particle-system model for cloth draping [J]. IEEE Computer Graphics and Applications, 1996, 16 (5):52-59. [百度学术]
HU J, CHEN S F, TENG J. Numerical drape behavior of circular fabric sheets over circular pedestals [J]. Textile Research Journal, 2000, 70 (7):593-603. CPP [百度学术]