网刊加载中。。。

使用Chrome浏览器效果最佳，继续浏览，你可能不会看到最佳的展示效果，

确定继续浏览么?

复制成功，请在其他浏览器进行阅读

摘要

本研究采用深度学习算法，对造纸废水处理过程的温室气体（GHG）排放进行建模与分析，以期为温室气体减排控制提供参考。结合造纸废水处理温室气体产生机理，在基准仿真1号模型（BSM1）的实验基础上，将深度神经网络（DNN）模型和长短期记忆网络（LSTM）模型用于造纸废水处理过程中温室气体排放建模与分析，以辅助温室气体在线监测和分析。结果表明，深度学习模型可以有效地捕捉温室气体排放的特征。模型验证结果R²>0.99，平均相对误差不超过1%。基于DNN的灵敏度分析结果表明，曝气强度、污泥排放量、溶解氧浓度及内循环流量是影响造纸废水处理过程温室气体排放的关键操纵变量，水质变量和操纵变量间的相互作用是影响温室气体排放的潜在因素。

关键词

深度神经网络; 长短期记忆; 造纸废水处理; 温室气体

造纸过程需要消耗大量的新鲜水，同时会产生含高浓度BOD的废水^[

1]。造纸废水中的BOD在微生物的分解作用下形成小分子的CO₂、CH₄和N₂O^{[参考文献 2

百度学术}2]，导致大量的温室气体（GHG）排放，妨碍了造纸工业的可持续发展。因此，控制造纸废水处理过程中的GHG排放成为了行业碳减排的重要任务。

建立GHG排放模型有助于改进在线测量技术和制定减排控制策略，而不干扰实际过程。城市废水处理过程N₂O排放的研究受到广泛关注。研究人员基于活性污泥模型（ASM）^[

3]，开发了一些动态机理模型，用于计算N₂O的排放^{[参考文献 4-5}4-5]。关于生物脱氮过程N₂O的形成机制，展开了相应研究^{[参考文献 6-7}6-7]。在ASM机理模型上拓展和改进N₂O动态机理模型，大多基于不同场景下的假设，适用性较差。数据驱动方法也被用于废水处理过程GHG排放的评估。基于现场和中试数据，利用人工神经网络建立了N₂O排放量的预测模型^{[参考文献 8

百度学术}8]。K均值聚类、主成分分析、随机森林等机器学习方法被用于研究废水生物脱氮过程中N₂O排放量与在线操作变量之间的相关性^{[参考文献 9

百度学术}9]。面对大量长期非线性动态废水数据，深度学习方法被广泛用于废水处理过程变量的预测^{[参考文献 10-11}10-11]。

目前相关研究提出的模型主要集中在对城市废水处理过程N₂O的建模。对于氮含量较低的造纸废水，其生化处理过程产生的N₂O远远少于CO₂，但厌氧处理过程中直接排放的CH₄往往被忽略。另外，由于生产端产品种类的切换和工艺条件的变化，造纸厂废水水质波动具有较大的不确定性，进一步导致废水处理过程GHG排放的不确定性^[

12]。这给造纸废水处理过程GHG减排带来了巨大的挑战。

深度学习作为最强大的机器学习工具之一，通过深度架构来学习和表示大数据的分层特征，在解决复杂过程建模问题中发挥重要作用。本研究通过机理和深度学习方法，建立完整的造纸废水处理过程GHG排放模型，为开发高效的造纸废水处理过程GHG减排方案提供依据，以促进造纸工业智能化和可持续发展。

1 实验

1.1　基于BSM1的造纸废水处理过程建模

基准仿真1号模型（BSM1）可以很好地描述废水生化处理过程中，不同物质的浓度变化及微生物的生长，被广泛应用于城市废水处理过程建模^[

13]。

BSM1是按照市政污水的负荷来设计的，而本研究对象为造纸工业废水，入水流量和污染物浓度均比市政废水较高。为使BSM1更适合工业废水处理过程，需要对其进行修正，以适应高负荷的工业废水处理过程。需要修正的值包括：反应动力学参数、反应器和沉淀池的尺寸及操纵变量的取值。

反应动力学参数主要受温度的影响，可采用Arrhenius公式对部分动力学参数进行修正^[

14]。设计参数和操纵变量的修正根据入水负荷决定。造纸废水的污染物负荷远高于BSM1模型中市政污水数据。废水厂的处理能力与设备尺寸之间不是简单的线性关系，并且操纵变量的修正也会导致处理能力的改变，这使得设备尺寸和控制变量的调整变得复杂。

为了确定最佳参数和操纵变量组合，采用现场水质和流量数据进行测试。通过调整设备尺寸和操纵变量，使用修正了动力学参数的BSM1进行开环仿真，记录每次仿真结果，并计算出水水质，水质达标率越高，表示所选取的设备尺寸和操纵变量越合适，迭代修正流程如图1所示。

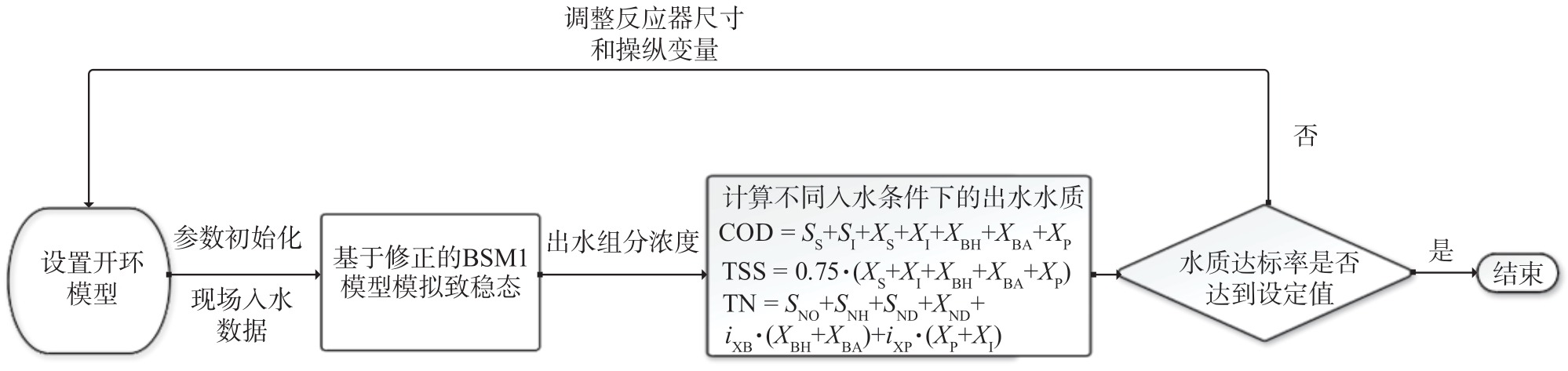
图1 BSM1模型修正流程图

Fig. 1 Flowchart of BSM1 correction

1.2　GHG机理模型

1.2.1　厌氧过程

厌氧反应器中，废水中的有机物一部分参与合成微生物细胞，另一部分则在厌氧条件下分解为CO₂和CH₄。另外，部分微生物通过内源性呼吸进一步转化为CO₂和CH₄。根据化学反应式的质量守恒关系，BOD去除过程中CO₂和CH₄的排放速率分别表示为 $M_{C O_{2}, B O D}^{A n}$ 和 $M_{C H_{4}, B O D}^{A n}$ ，其计算分别见式(1)和式(2)^[

15]。

M_{C O_{2}, B O D}^{A n} = 0.27 \times [Q_{i n}^{A n} \cdot (B O D_{i n}^{A n} - B O D_{o u t}^{A n}) - 1.42 P_{b i o}^{A n}]

（1）

M_{C H_{4}, B O D}^{A n} = 0.25 \times [Q_{i n}^{A n} \cdot (B O D_{i n}^{A n} - B O D_{o u t}^{A n}) - 1.42 P_{b i o}^{A n}]

（2）

式中， $Q_{i n}^{A n}$ 表示进入厌氧反应器的废水流量， $B O D_{i n}^{A n}$ 和 $B O D_{o u t}^{A n}$ 分别表示进出厌氧反应器的BOD浓度， $P_{b i o}^{A n}$ 表示厌氧过程由于BOD氧化所生成的微生物的量，具体计算见式(3)。

P_{b i o}^{A n} = \frac{0.004 M_{C_{5} H_{7} O_{2} N}}{0.02 M_{C_{10} H_{19} O_{3} N}} \cdot Q_{i n}^{A n} \cdot (B O D_{i n}^{A n} - B O D_{o u t}^{A n})

（3）

内源性呼吸过程的CO₂和CH₄排放速率分别表示为 $M_{C O_{2}, V S S}^{A n}$ 和 $M_{C H_{4}, V S S}^{A n}$ ，其计算分别见式(4)和式(5)。

M_{C O_{2}, V S S}^{A n} = 0.58 M_{V S S, d e c a y}^{A n}

（4）

M_{C H_{4}, V S S}^{A n} = 0.35 M_{V S S, d e c a y}^{A n}

（5）

式中， $M_{V S S, d e c a y}^{A n}$ 表示厌氧阶段微生物通过自身内源性呼吸所衰变微生物的量。

1.2.2　好氧过程

好氧过程与厌氧过程类似，也包含有机物的氧化分解和微生物的内源呼吸，这2个过程CO₂排放速率分别表示为 $M_{C O_{2}, B O D}^{A e}$ 和 $M_{C O_{2}, V S S}^{A e}$ ，其计算分别见式(6)和式(7)。

M_{C O_{2}, B O D}^{A e} = 0.33 \times (\frac{Q_{i n}^{A e} \cdot (B O D_{i n}^{A e} - B O D_{o u t}^{A e})}{f} - 1.42 P_{b i o}^{A e})

（6）

M_{C O_{2}, V S S}^{A e} = 1.56 M_{V S S, d e c a y}^{A e}

（7）

式中， $Q_{i n}^{A e}$ 表示进入厌氧反应器的废水流量， $B O D_{i n}^{A e}$ 和 $B O D_{o u t}^{A e}$ 分别表示进出厌氧反应器的BOD浓度， $f$ 表示为5天生化需氧量与总生化需氧量的比值， $M_{v s s, d e c a y}^{A e}$ 为好氧阶段微生物通过自身内源性呼吸所衰变微生物的量。

在好氧环境下还会发生硝化和反硝化反应，其中硝化过程会消耗CO₂，反硝化过程会生成CO₂，其排放速率分别用 $M_{C O_{2}, n i t}^{A e}$ 和 $M_{C O_{2}, d e n i t}$ 表示，计算分别见式(8)和式(9)。

M_{C O_{2}, n i t}^{A e} = 0.25 \times [Q_{i n}^{A e} \cdot (T K N_{i n}^{A e} - T K N_{o u t}^{A e}) - 0.12 \cdot P_{b i o}^{A e}]

（8）

M_{C O_{2}, d e n i t} = 2.81 \cdot Q_{i n}^{A e} \cdot N O_{x}

（9）

式中， $T K N_{i n}^{A e}$ 和 $T K N_{o u t}^{A e}$ 分别表示进出好氧反应器的凯氏氮浓度， $N O_{x}$ 表示硝化过程被硝化的氨态氮的量，可通过质量守恒求得。

整个生物脱氮过程N₂O的排放速率 $M_{N_{2} O}$ ，可用排放因子 $R_{N_{2} O}$ 乘以总氮的去除量进行计算，如式(10)所示。

M_{N_{2} O} = R_{N_{2} O} \cdot Q_{i n} \cdot (T N_{i n} - T N_{o u t})

（10）

式中， $Q_{i n}$ 表示进入废水处理系统的废水流量， $T N_{i n}$ 和 $T N_{o u t}$ 分别表示进出整个废水处理系统的总氮浓度。

1.3　深度学习模型

受生产过程产品种类的切换和工艺条件变化的影响，造纸废水水质波动具有较大的不确定性。复杂的造纸废水来源，使废水处理过程形成了一个多输入、多输出、高度非线性、处理机理复杂的系统^[

15]。基于BSM1的机理模型能够计算实际温室气体排放量，但其参数优化和设计的计算成本过高^{[参考文献 16

百度学术}16]。建立过程机理模型的机器学习代理模型可以解决这类问题。但传统的机器学习在处理有限样本时，容易出现过拟合和梯度消失等问题。深度学习方法通过引入Dropout函数缓解过拟合，采用ReLU激活函数解决梯度消失问题^{[参考文献 17

百度学术}17]，在过程建模和预测领域有广泛应用。

深度神经网络（DNN）是一种典型的深度学习模型，包括多层结构、非线性变换、层级特征学习和逐层抽象表示，将其用于处理复杂数据和任务，能够对多输入多输出系统进行建模，表现出强大的非线性拟合能力。长短期记忆网络（LSTM）是一种循环神经网络，被广泛应用于时序数据的动态预测。LSTM通过引入门结构来控制信息传递路径及累积速度，可有效解决简单循环神经网络存在的梯度爆炸或消失问题，可处理时间序列数据的依赖关系。

因此，本研究针对造纸废水处理系统高度非线性的特点，基于过程仿真和温室气体机理模型，建立了入水和操纵变量与温室气体排放之间的DNN过程模型，为过程分析和优化控制提供基础。针对造纸废水水质波动的不确定性，导致温室气体排放的不确定性，基于动态BSM1仿真得到的温室气体时序数据，建立了LSTM时序预测模型，以期辅助温室气体的在线监测和动态优化控制。

1.4　全局灵敏度分析

全局灵敏度分析（GSA）方法能够量化单变量或多变量相互作用对输出参数的贡献程度，稳定性较高, 在过程建模分析领域有广泛的应用。常用的GSA方法有Morris、FAST、Sobol和Kucherenk等方法。其中，Sobol和Kucherenko方法具有数值稳定性、非线性、交互效应以及在高维空间适用性强^[

18-19]等优点，非常适用于多变量、非线性、强耦合的造纸废水处理系统的分析。

1.4.1　Sobol 方法

Sobol方法^[

18]是一种基于方差分解的GSA方法，可以通过参数对输出方差的贡献比例进行灵敏度分级。Sobol法的核心思想是将模型设为单一参数及各参数间互相组合的函数，可分别得到参数一阶、二阶及更高阶的灵敏度。最常用的指数是一阶Sobol指数

S_{i}

和全局Sobol指数

S_{T i}

。Sobol的一阶指数通过条件方差

V a r [E (y |x_{i})]

量化了输入变量

x_{i}

对总输出方差

V a r [y]

的单独贡献，其计算见式(11)。

S_{i} = \frac{V a r [E (y |x_{i})]}{V a r [y]}

（11）

全局指数 $S_{T i}$ 量化了输入变量 $x_{i}$ 对总输出方差的总贡献，还包括由于该输入变量与其他输入变量的交互作用而产生的贡献。该指数的计算如式(12)所示。

S_{T i} = 1 - \frac{[V a r E (y |x_{- i})]}{V a r [y]}

（12）

其中， $[V a r E (y |x_{- i})]$ 表示除 $x_{i}$ 外所有变量的条件方差。全局指数和一阶指数之差可作为模型其他输入变量于 $x_{i}$ 之间相互作用对模型输出影响的度量。

1.4.2　Kucherenko方法

Kucherenko方法考虑输入变量之间的相互依赖关系，将输入空间X划分为2个互补子集 $X_{y}$ 和 $X_{z}$ ，并将模型的总输出方差分解为 $Y = f (X)$ ^[

19]。一阶Kucherenko指数和全局Kucherenko指数计算分别见式(13)和式(14)。

S_{i} = \frac{V a r [E_{z} (f (X_{y}, {\bar{X}}_{z}))]}{V a r [Y]}

（13）

S_{T i} = \frac{E_{z} [V a r [Y |f ({\bar{X}}_{y}, X_{z})]]}{V a r [Y]}

（14）

式中， $X_{z}$ 和 ${\bar{X}}_{z}$ 分别表示从先验已知的联合概率密度函数和先验已知的条件分布函数生成的随机向量。

2 结果与讨论

2.1　GHG排放特征

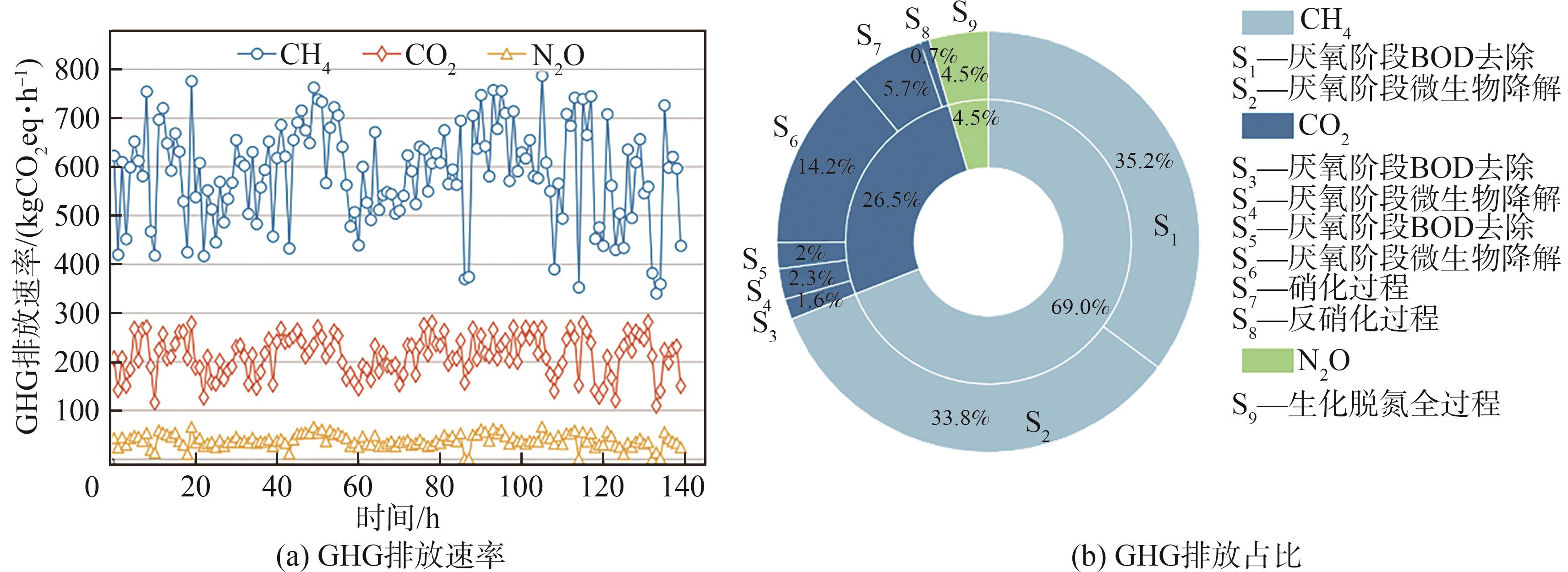
基于稳态仿真结果，计算了不同入水条件和操作条件下CO₂、CH₄和N₂O的排放速率（按CO₂当量计），并统计了各个子过程产生温室气体的分布和比例，如图2所示。从图2(a)可以看出，排放速率随着入水流量和污染物浓度的变化而变化。CH₄是造纸废水生化处理过程对温室效应贡献最大的温室气体，其平均排放速率约为600 kgCO₂eq/h。CO₂的贡献次之，其平均排放速率约为200 kgCO₂eq/h，N₂O的贡献最小，其平均排放速率只有40 kgCO₂eq/h。在A/O工艺中，厌氧反应器是主要的污染物降解场所，废水中的有机物大部分在厌氧生化反应器内被厌氧菌分解为CH₄和CO₂，而好氧反应器起到次要降解作用，进一步降低出水COD。

图 2 温室气体排放计算结果

Fig. 2 Calculation results of GHG

从图2(b)可以看出，整个生化处理过程CH₄对温室效应的贡献达69.0%，CO₂占26.5%，N₂O只占4.5%。其中产生CH₄的2个子过程，也是所有子过程中温室效应贡献最大的2个过程，分别贡献了35.2%和33.8%。产生CO₂的过程中，好氧反应器内内源性衰变的贡献最大。硝化过程消耗的CO₂占比最少，也是唯一一个会减少GHG排放的过程。尽管CH₄的贡献最大，但其来源只有2个子过程，CO₂的来源有6个过程。从反应动力学角度来看，废水处理各个过程之间存在相互联系。如含氮有机物的分解会产生氨态氮，而氨氮是硝化过程的反应物，硝化过程产生的硝态氮又会参与到反硝化过程。这些过程之间的相互作用耦合对制定温室气体减排的方案不可忽视。造纸废水生化处理过程减排方案的制定应该综合考虑多个过程之间的联系，CO₂和N₂O的控制也比较关键。

2.2　DNN预测结果

图3展示了4个最优DNN模型的温室气体排放强度预测结果。由图3可以看出，每处理1 L的造纸废水，约直接排放0.1~0.45 kgCO₂、0.3~1.2 kgCO₂eq的CH₄，以及0.015~0.08 kgCO₂eq的N₂O，总GHG排放在0.5~1.7 kgCO₂eq范围内。总体上来看，4个DNN模型在多数情况下可以替代GHG机理模型，平均相对误差（MAPE）均在1%以内。

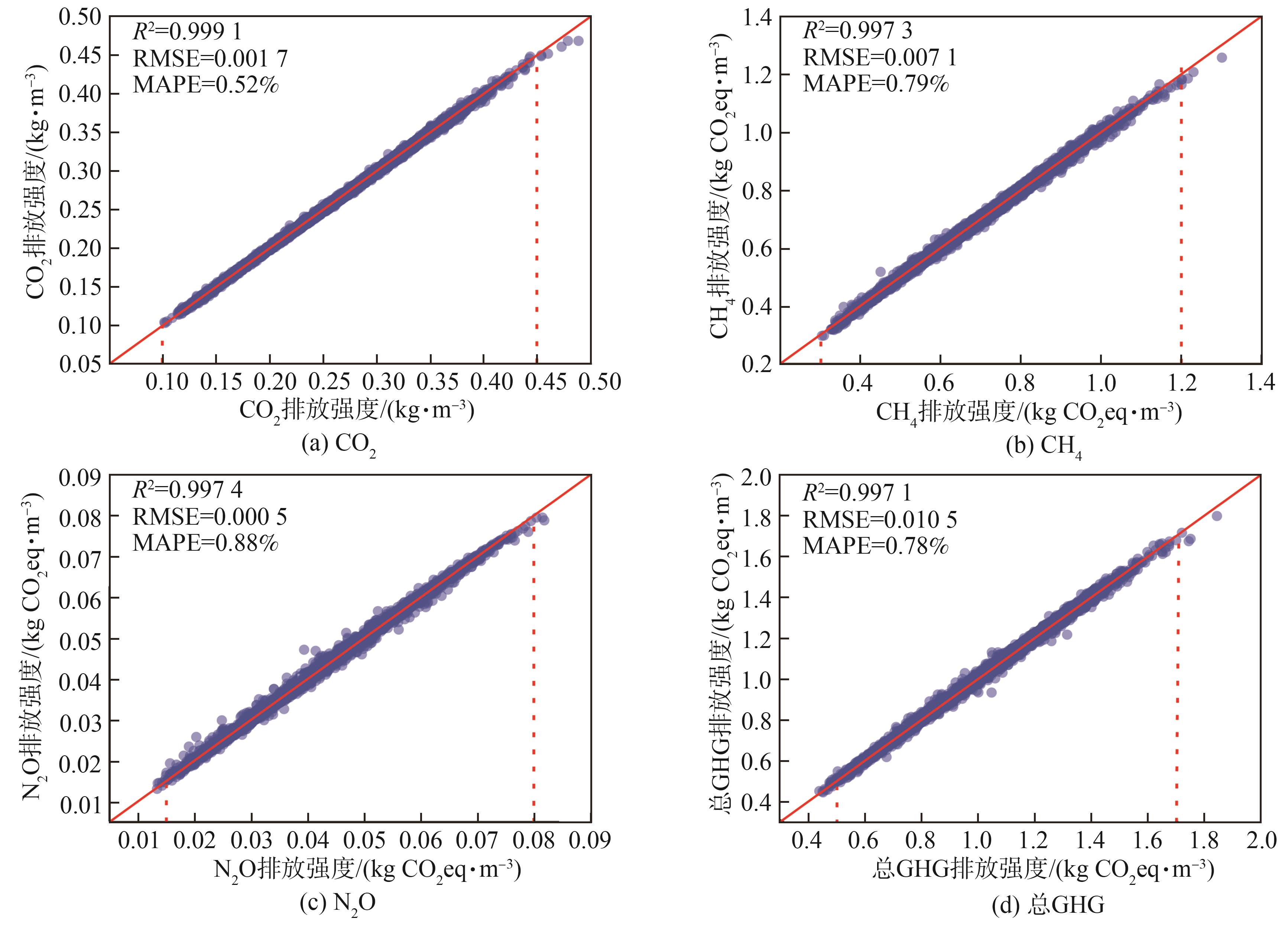
图 3 基于DNN的GHG排放计算模型

Fig. 3 GHG emission calculation model based on DNN

本研究中，每次训练预测CO₂、CH₄和N₂O模型所采用的输入数据、模型结构、激活函数、超参数及训练次数均保持一致，但预测不同的目标确得到了不同精度的模型。这表明造纸废水处理过程不同温室气体产生机理的复杂程度存在一定的差异，模型的性能越差，对应的温室气体产生机理越复杂。在不断调整参数以训练出更高精度模型的过程中，发现预测N₂O排放的模型性能几乎总是最差的。这表明造纸废水处理过程N₂O的产生机理最为复杂。

此外，本研究将DNN模型与支持向量回归（SVR）和随机森林（RF）2个传统的机器学习算法进行了对比。保持模型训练过程的训练集和测试集一致，在预测总温室气体排放强度时，模型的评价指标结果如表1所示。

表 1 DNN与传统机器学习对比

Table 1 DNN versus traditional machine learning

学习算法	R²	RMSE	MAPE
SVR	0.789 4	0.001 2	0.129 6
RF	0.990 6	0.011 59	0.030 1
DNN	0.997 1	0.010 5	0.007 8

从表1对比结果可以看出，SVR的效果最差，模型的拟合优度R²相对最小，均方误差（RMSE）和MAPE相对较大。RF和DNN的R²均在0.99以上，拟合效果较好，但RF的平MAPE比误差远远大于DNN模型。总体来看，DNN模型的性能最优，更适用对造纸废水处理过程温室排放建模。

2.3　LSTM预测结果

图4展示了LSTM预测动态GHG排放速率结果。动态条件下，GHG排放速率比稳态模拟条件下计算的结果小，排放总量在200~600 kgCO₂eq/h之间波动。这是因为动态模拟情况下，水质和流量随着时间发生变化，这种波动导致废水处理系统在不同状态之间频繁切换，使整个系统的稳定性降低，污染物的去除量降低，GHG排放也减少。

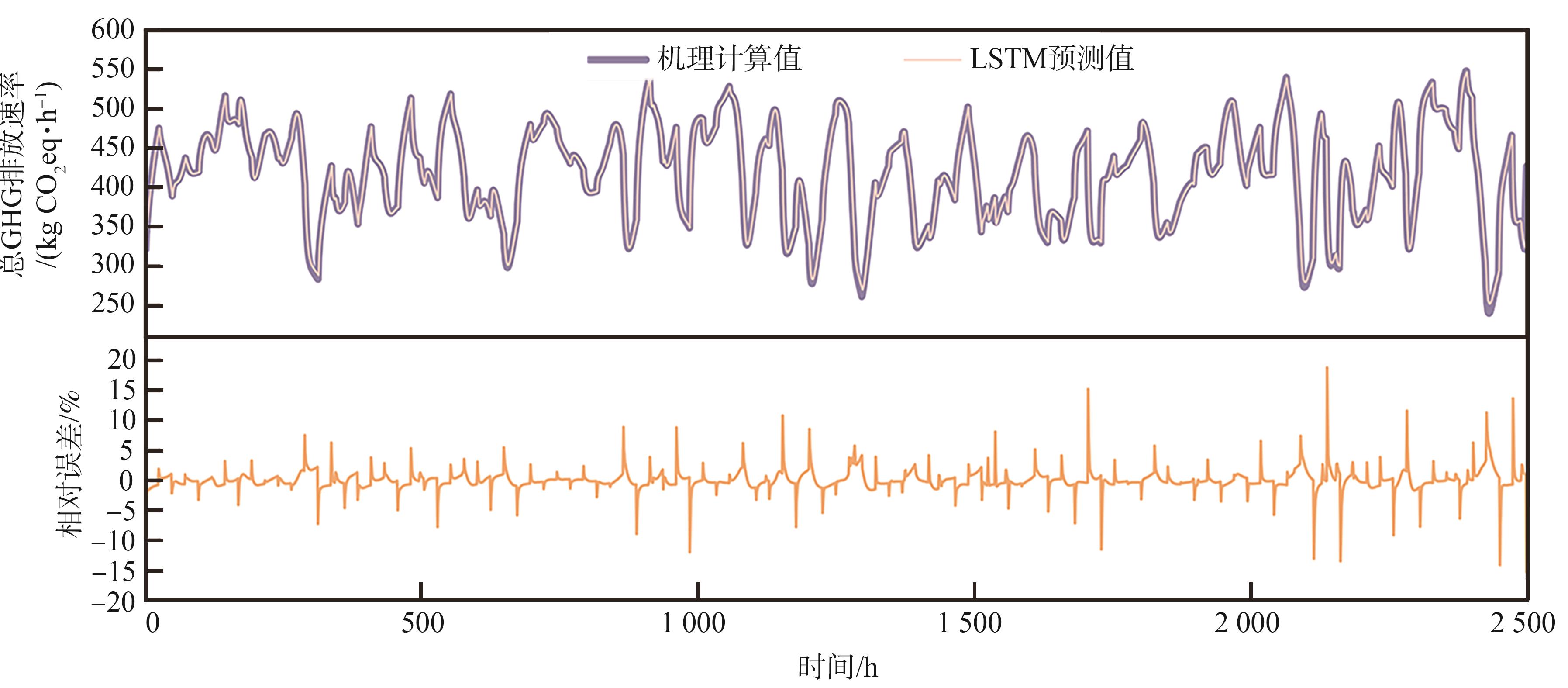
图 4 LSTM预测动态GHG排放速率

Fig. 4 Dynamic GHG emissions rate predicted by LSTM

LSTM描述了废水处理过程的GHG排放动态变化特征，和机理模型计算的结果之间具有良好的相关性，平均相对误差也较小。从相对误差的变化情况来看，在预测时段内LSTM预测结果的相对误差基本在-5%~5%之间波动。但在波峰和波谷处相对误差较大，最大相对误差接近20%。另外，随着预测时段向前延伸，在峰点和谷点的相对误差绝对值总体上呈现逐渐增大的趋势。这是因为在输入采样时，笔者设定了采样范围使得BSM1仿真过程尽可能在符合实际情况的条件下稳定运行。因此，训练模型过程主要是对正常入水条件下的温室气体排放进行拟合，忽略了异常入水情况下的温室气体动态排放特征，这导致了LSTM在异常条件下性能下降。

DNN过程模型和LSTM预测模型均可以描述废水处理过程GHG排放的特征。DNN描述过程工艺参数与目标值之间的对应关系，能反应过程机理的复杂程度，但是建立DNN模型需要多维度的过程工艺参数数据作为模型的输入。LSTM对预测目标的时间序列进行分段，构建时间尺度上的映射关系，描述预测目标随时间变化的动态特征，建立LSTM预测模型只需要预测目标的时间序列数据，但无法体现过程反应机理。因此，DNN模型适用于过程建模，能够反应实际过程的复杂程度和工艺特征。LSTM模型从时间尺度上反映过程动态变化特征，适用于对时序变量的短期预测。

2.4　GSA分析结果

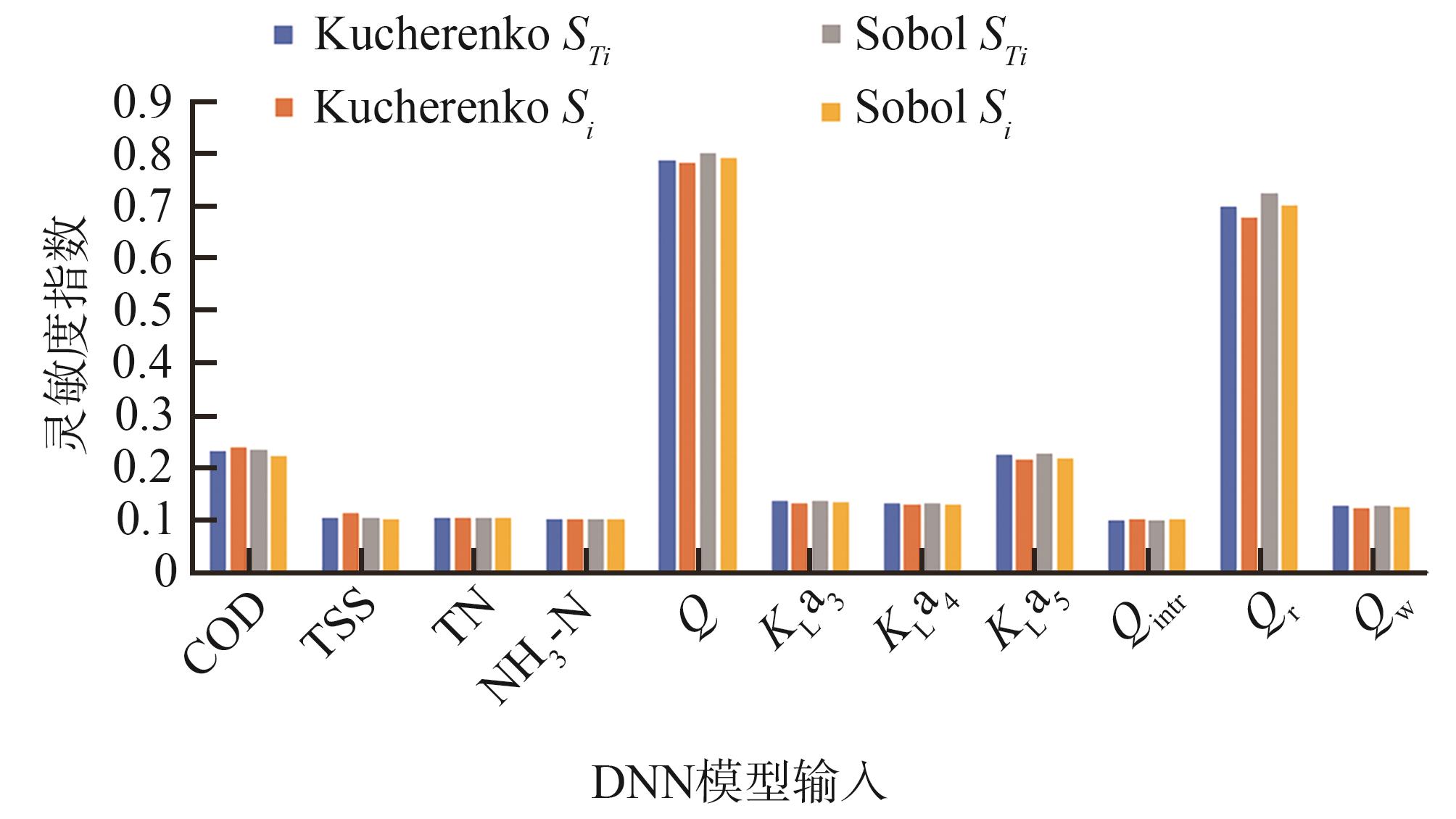
本研究使用GSA确定了总GHG排放速率贡献最大的因素。基于DNN模型，采用Sobol指数和Kucherenko指数2种不同的GSA方法。2种方法的采样均保持操纵变量之间相互独立。Sobol方法采样保证水质数据之间也相互独立。Kucherenko方法在采样过程中保证了水质数据之间的相关性。图5展示了GHG排放速率的Sobol和Kucherenko灵敏度分析的结果。

图 5 基于DNN的GHG排放强度灵敏度分析结果

Fig. 5 GHG emission rate sensitivity analysis results based on DNN

图5中K_La₃、K_La₄和K_La₅分别表示BSM1中3个好氧反应器的氧传递系数，用于控制曝气强度来调节反应器内溶解氧浓度；Q_intr和Q_r分别表示内、外循环流量；Q_W表示污泥排出系统的速率。GSA表明入水水质和流量对过程GHG排放量的方差贡献度要大于控制变量的影响。其中K_La₅和Q_W是影响GHG排放的关键控制变量。流量Q和COD是影响GHG排放的关键入水变量。Sobol指数和Kucherenko指数之间的差异并不明显，这表明水质变量相互依赖关系对过程GHG的排放影响并不重要。另外，关键变量的一阶指数 $S_{i}$ 和全局指数 $S_{T i}$ 之间存在一定差距，这表明废水处理系统过程参数之间存在的交互作用是影响GHG排放的潜在因素。

3 结论

本研究建立了基于BSM1的造纸废水处理过程温室气体（GHG）排放机理模型，进一步结合深度神经网络（DNN）模型和长短期记忆网络（LSTM）预测模型，对造纸废水处理过程不同温室气体的产生进行了全局灵敏度分析。

3.1　CH₄是造纸废水A/O生化处理过程对温室效应贡献最大的气体，每处理1 m³的造纸废水直接排放约0.35~1.7 kgCO₂eq的GHG。

3.2　深度学习算法揭示了过程变量与GHG排放之间的联系以及动态变化特征，DNN模型R²在0.99以上，LSTM相对误差集中在5%以内，能够满足GHG减排控制、优化和辅助在线监测的需要。

3.3　曝气强度（K_La）和污泥排放速率（Q_W）是影响GHG排放的关键操纵变量，变量间的相互作用是影响GHG排放的潜在因素，是实现造纸企业废水处理减污降碳最优化运行的关键。

参考文献

徐峻，李军，陈克复. 制浆造纸行业水污染全过程控制技术理论与实践［J］. 中国造纸， 2020， 39（4）： 69-73. [百度学术]

XU J， LI J， CHEN K F. Whole-process Control of Water Pollution in Theory and Practices for Pulp and Paper Industry［J］. China Pulp & Paper， 2020， 39（4）： 69-73. [百度学术]

张欣，张放，蔡慧，等. 典型制浆造纸厂的CO₂排放及碳强度的算法和分析［J］中国造纸学报， 2019， 34（1）： 36-42. [百度学术]

ZHANG X， ZHANG F， CAI H， et al. Calculation and Analysis of CO₂ Emissions and Carbon Intensity of a Typical Integrated Paper Mill in China［J］. Transactions of China Pulp and Paper， 2019， 34（1）： 36-42. [百度学术]

HENZE M， GUJER W， MINO T， et al. Activated sludge models ASM1， ASM2， ASM2d and ASM3 ［M］. London： IWA Publishing， 2000：6-15. [百度学术]

BLOMBERG K， KOSSE P， MIKOLA A， et al. Development of an Extended ASM3 Model for Predicting the Nitrous Oxide Emissions in a Full-scale Wastewater Treatment Plant［J］. Environmental Science & Technology， 2018， 52（10）： 5803-5811. [百度学术]

MASSARA T M， SOLíS B， GUISASOLA A， et al. Development of an ASM2d-N₂O model to describe nitrous oxide emissions in municipal WWTPs under dynamic conditions［J］. Chemical Engineering Journal， 2018， 335： 185-196. [百度学术]

TERADA A， SUGAWARA S， HOJO K， et al. Hybrid Nitrous Oxide Production from a Partial Nitrifying Bioreactor： Hydroxylamine Interactions with Nitrite［J］. Environmental Science & Technology， 2017， 51（5）： 2748-2756. [百度学术]

HUANG X， XU Y， HE T， et al. Ammonium transformed into nitrous oxide via nitric oxide by Pseudomonas putida Y-9 under aerobic conditions without hydroxylamine as intermediate［J］. Bioresource Technology， 2019， 277： 87-93. [百度学术]

SUN S， BAO Z， LI R， et al. Reduction and Prediction of N₂O Emission from an Anoxic/Oxic Wastewater Treatment Plant Upon DO Control and Model Simulation［J］. Bioresource Technology， 2017， 244： 800-809. [百度学术]

VASILAKI V， VOLCKE E I P， NANDI A K， et al. Relating N₂O emissions during biological nitrogen removal with operating conditions using multivariate statistical techniques［J］. Water Research， 2018， 140： 387-402. [百度学术]

裴力锋，陈伟杰，徐敬生，等. 基于自注意力机制的污水处理厂精确加药模型预测控制［J］环境工程， 2023， 41（11）：84-92，140. [百度学术]

PEI L F， CHEN W J， XU J S， et al. Model predictive contorl for accurate dosing in wastewater treatment plants based on self-attention mechanism［J］ Environmental Engineering， 2023， 41（11）：84-92，140. [百度学术]

HWANGBO S， AL R， CHEN X， et al. Integrated Model for Understanding N₂O Emissions from Wastewater Treatment Plants： A Deep Learning Approach［J］. Environmental Science & Technology， 2021， 55（3）： 2143-2151. [百度学术]

陆造好，满奕，李继庚，等. 基于深度强化学习的造纸废水处理过程多目标优化［J］. 中国造纸， 2023，42（3）：13-22，103. [百度学术]

LU Z H， MAN Y， LI J G， et， al. Multi-objective Optimization of Papermaking Wastewater Treatment Process Based on Deep Reinforcement Learning［J］. China Pulp & Paper， 2023，42（3）：13-22， 103. [百度学术]

COPP J B. The COST Simulation Benchmark-Description and Simulator Manual［J］. Office for Official Publications of the European Community Luxembourg， 2001， 1： 1-58. [百度学术]

MAN Y， SHEN W， CHEN X， et al. Dissolved oxygen control strategies for the industrial sequencing batch reactor of the wastewater treatment process in the papermaking industry［J］. Environmental Science： Water Research & Technology， 2018， 4（5）： 654-662. [百度学术]

郑鸿泽，何正磊，洪蒙纳，等. 造纸废水处理过程温室气体排放代理模型研究［J］.中国造纸学报， 2023， 38（2）： 59-68. [百度学术]

ZHENG H Z， HE Z L， HONG M N， et al. Study on Surrogate Model of Greenhouse Gas Emission in Papermaking Wastewater Treatment Process［J］. Transactions of China Pulp and Paper， 2023， 38（2）： 59-68. [百度学术]

NEWHART K B， HOLLOWAY R W， HERING A S， et al. Data-driven performance analyses of wastewater treatment plants： A review［J］. Water Research， 2019， 157： 498-513. [百度学术]

马源，曾淦宁，戴孟铮，等. 基于DNN的活性炭吸附预测及性能评价［J］. 化学工程， 2022， 50（12）： 27-31. [百度学术]

MA Y， ZENG G N， DAI M Z， et al. Construction of deep neural network aided adsorption prediction and performance evaluation［J］. Chemical Engineering， 2022， 50（12）： 27-31. [百度学术]

SOBOL’ I M. Global sensitivity indices for nonlinear mathematical models and their Monte Carlo estimates［J］. Mathematics and Computers in Simulation， 2001， 55（1）： 271-280. [百度学术]

KUCHERENKO S， TARANTOLA S， ANNONI P. Estimation of global sensitivity indices for models with dependent variables［J］. Computer Physics Communications， 2012， 183（4）： 937-946. CPP [百度学术]

基于DNN⁃LSTM的造纸废水处理过程温室气体排放分析模型

摘要

关键词

1 实验

1.1 基于BSM1的造纸废水处理过程建模

1.2 GHG机理模型

1.3 深度学习模型

1.4 全局灵敏度分析

2 结果与讨论

2.1 GHG排放特征

2.2 DNN预测结果

2.3 LSTM预测结果

2.4 GSA分析结果