网刊加载中。。。

使用Chrome浏览器效果最佳，继续浏览，你可能不会看到最佳的展示效果，

确定继续浏览么?

复制成功，请在其他浏览器进行阅读

摘要

本课题基于奇异非混沌优化（SNO）改进了极限学习机（ELM），并用于解决纸机横幅（CD）定量系统的耦合问题。首先，采用基于分段逻辑映射的SNO方法，对输入层和隐藏层之间随机生成的权重和阈值进行优化，解决了ELM优化不足的缺点。然后，设计奇异非混沌优化极限学习机（SNOELM）解耦器，对多变量系统进行解耦。最后，将其与已提出的改进ELM、鲸鱼优化极限学习机（WOELM）和粒子群优化极限学习机（PSOELM）进行了比较。仿真结果表明，SNOELM解耦方法比ELM具有更好的优化能力，比WOELM和PSOELM具有更高的解耦精度和更快的解耦速度。

关键词

纸张定量; 静态解耦; 极限学习机; 优化

定量是单位面积纸张的质量，是评价造纸过程中纸张质量的最重要性能指标之一^[

1]。高速印刷机的广泛使用对纸张纤维的均匀分布也有更严格的要求。纸张纤维的均匀分布主要体现在定量分布上^{[参考文献 2

百度学术}2]，因此，改善定量分布的均匀性可以有效地维持高速打印机的稳定工作，提高打印效率和质量。同时，为了保护环境、节约成本，纸和纸板的低定量化是一种必然趋势，因此，定量的控制尤为重要。目前，纸机横幅（CD）定量控制是改善定量分布和实现纸张低定量的主要控制方法^{[参考文献 3

百度学术}3]。

CD定量控制通过调节安装在稀释水流浆箱上的执行器实现^[

4]。执行器数量众多，并紧密布置在稀释水流浆箱上。当执行器向纸浆中注入稀释水时，由于流体的冲击和扩散作用，相邻区域的纸浆浓度也会受到影响，显示出强烈的耦合特性^{[参考文献 5

百度学术}5]。执行器之间的耦合特性不利于CD定量的均匀分布，因此有必要找到一种有效且快速的解耦方法来维持定量的均匀分布。目前，神经网络因其具有处理非线性输出的优点，已广泛应用于解耦算法。Sun等人^{[参考文献 6

百度学术}6]针对无轴承永磁同步电机（BPMSM）提出了一种使用神经网络逆（NNI）方法的新型解耦方案，以实现BPMSM系统的快速响应和高精度性能。Dong等人^{[参考文献 7

百度学术}7]针对系统的非线性、死区和强耦合特性，提出了一种基于神经网络和预测原理的解耦方法，取得了较好的控制效果。上述研究均是基于反向传播（BP）算法的神经网络，然而，这种基于梯度的迭代学习算法通常速度较慢，阻碍了其广泛应用。近年来，极限学习机（ELM）^{[参考文献 8

百度学术}8]作为一种高效的解耦方式已经被应用于多变量解耦。与BP神经网络相比，ELM简化了学习参数的设置，并通过设置输入层和隐藏层的神经元权重参数和阈值参数，来更新单个隐藏层的权重。因此，ELM在学习速度和泛化能力方面具有优势。虽然ELM训练速度快，泛化能力强，但存在优化不足和多重共线性等问题。因此，大量的优化算法被应用于ELM，如粒子群优化^{[参考文献 9

百度学术}9]、遗传算法^{[参考文献 10

百度学术}10]和鲸鱼优化算法^{[参考文献 11

百度学术}11]。

奇异非混沌动力学是非线性动力学领域的研究热点之一^[

12]，这是一种有边界的不稳定动力学行为。奇异非混沌系统产生的奇异非混沌序列，表现出遍历性和对控制参数的敏感依赖性。因此，控制参数的微小变化将导致未来动力学行为的巨大差异。基于上述特点，奇异非混沌理论已被应用于许多领域。优化是奇异非混沌动力学研究的一个重要应用领域^{[参考文献 13

百度学术}13]。基于奇异非混沌动力学的优化算法具有易于实现、执行时间短和脱离局部最优的优点。

针对CD定量系统的强耦合问题，本课题首次将奇异非混沌动力学应用于极限学习机，并提出了一种基于奇异非混沌优化极限学习机（SNOELM）的分布式解耦算法，以提高ELM的性能，包括解耦精度和解耦速度。

1 极限学习机及其改进算法

1.1　极限学习机

极限学习机（ELM）是一种基于广义逆矩阵新的单隐层前馈神经网络，具有良好的泛化性能和快速学习能力。经典的BP神经网络基于梯度下降法调整权重和阈值。而ELM的权值和阈值是人为设置的，可以大大提高网络的训练速度。图1显示了极限学习机网络结构。X_i=[x_i₁, x_i₂, …, x_im]是ELM的第i个m维输入。W_m_·_z和β_z_·_l分别是输入权重和输出权重。Y_i=[y_i₁, y_i₂, …, y_i_l]是ELM的第i个l维输出，与X_i关系见式(1)。

Y_{i}

\sum_{j = 1}^{z} β_{j} g (X_{i} \cdot w_{j} + b_{j})

（1）

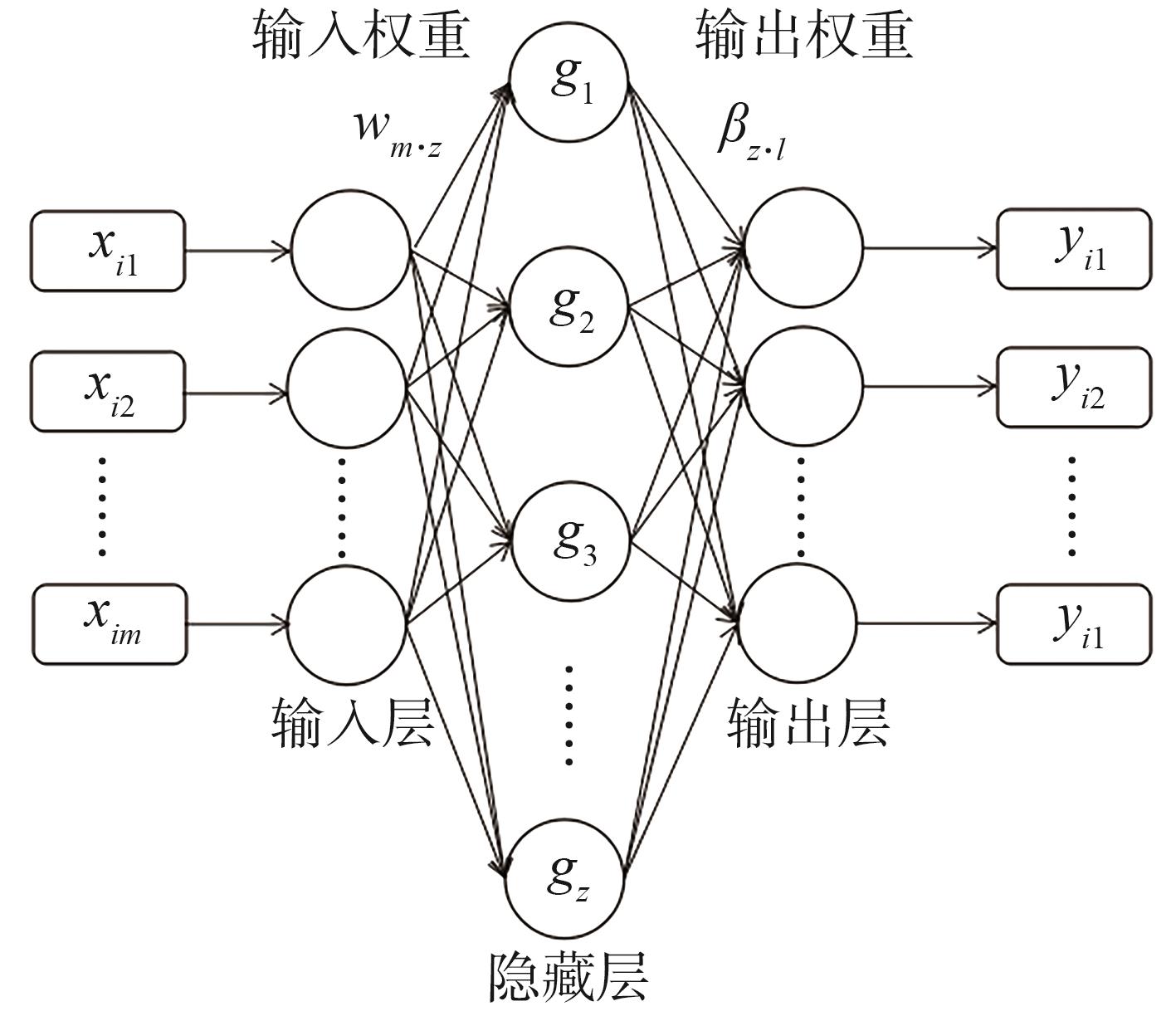
图1 ELM网络结构

Fig. 1 Network structure of ELM

其中，b_j是第j个隐藏层神经元的偏置。g(Z)是隐藏层的激活函数，通常用sigmoid函数表示，见式(2)。

g (Z)

\frac{1}{1 + e^{- Z}}

（2）

在ELM中，输入层和隐藏层之间的权重和偏置由人工设置或随机生成。在设置权重和偏置后，输出层的权重可以通过式(3)计算。

β = H^{- 1} T

（3）

H是隐藏层节点的输出，其计算见式(4)。

H

{[\begin{array}{l} g (w_{1} \cdot X_{1} + b_{1}) \dots g (w_{z} \cdot X_{1} + b_{z}) \\ ⋮ \dots ⋮ \\ g (w_{1} \cdot X_{n} + b_{1}) \dots g (w_{z} \cdot X_{n} + b_{z}) \end{array}]}_{n \cdot z}

（4）

对于式(3)和式(4)，β=[β₁^T, β₂^T, …, β_z^T]_l_·_z^T是输出权重，T=[T₁^T, T₂^T, …, T_n^T]_l_·_n^T是预期输出。

1.2　奇异非混沌优化

奇异非混沌优化算法是基于奇异非混沌动力学的现代启发式优化算法。优化过程是模拟一个奇异非混沌吸引子随时间变化的运动过程。基于确定性系统中奇异非混沌动力学的遍历性和伪随机性，得到目标函数的最大值或最小值，并得到最优解。本节使用的奇异非混沌系统如式(5)所示。

\begin{array}{l} x (n + 1) = \{\begin{array}{l} (a + b c o s (2 π φ (n))) \cdot x (n) \cdot (1 - x (n)) i f x (n) < 1 / 2 \\ 1 / 2 i f x (n) = 1 / 2 \\ (a + b c o s (2 π φ (n))) \cdot x (n) \cdot (x (n) - 1) + 1 i f x (n) > 1 / 2 \end{array} \\ φ (n + 1) = φ (n) + ω (m o d 1) \end{array}

（5）

式中，n为迭代次数，a和b为系统控制参数。奇异非混沌吸引子通过Lyapunov指数λ_x和相敏感函数Γ_n来表征。具体表达式分别见式(6)和式(7)。

λ_{x} = \underset{N \to \infty}{l i m} \frac{1}{N} \sum_{i = 1}^{N} l n |\frac{\partial f}{\partial x_{i}}|

（6）

Γ_{n} (a, b) = \underset{x_{0}, φ_{0}}{m i n} (\underset{0 \leq n \leq N}{m a x} |\frac{\partial x (n)}{\partial φ}|) = n^{μ}

（7）

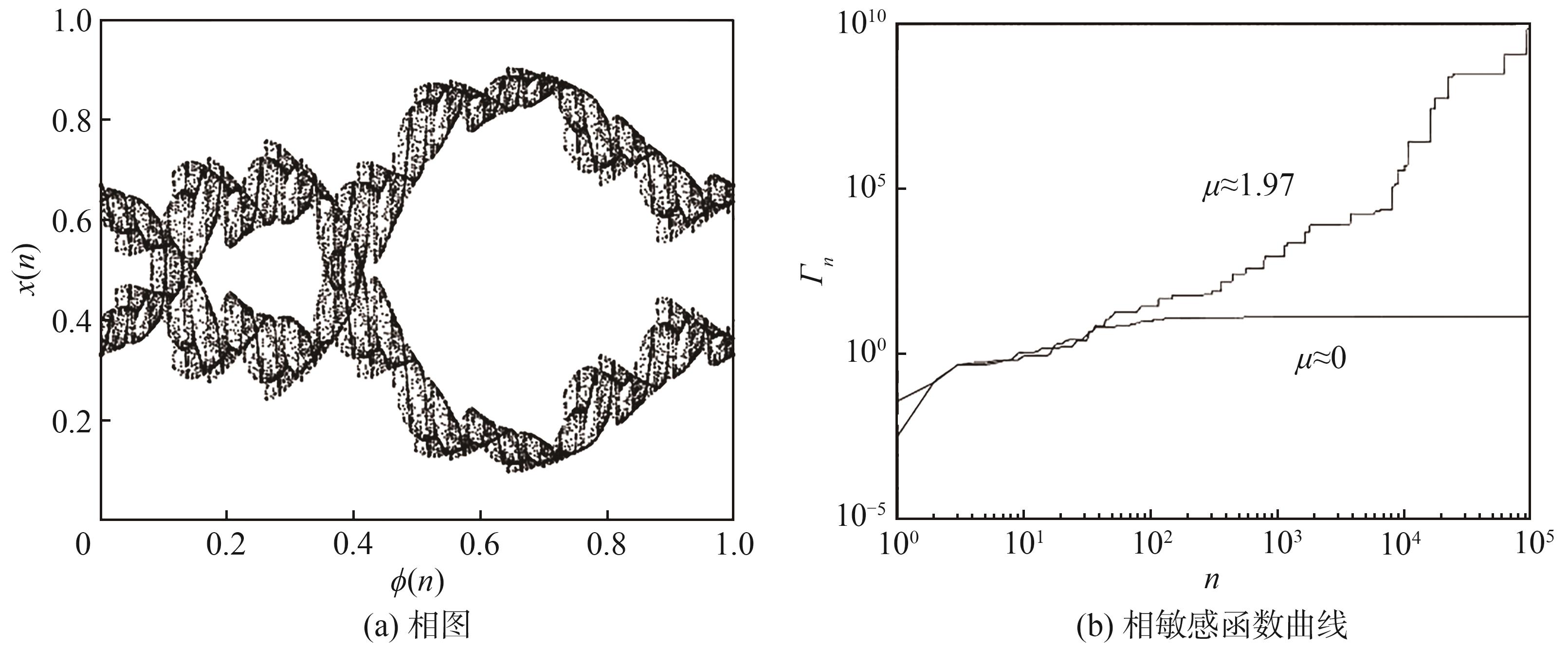
奇异非混沌吸引子具有1个负的Lyapunov值和正的μ值。当参数a和b固定为a=3.09和b=0.55时，图2(a)显示了1个分形吸引子，其最大Lyapunov指数为-0.011，相位灵敏度指数为1.97（如图2(b)所示）。因此确认该分形吸引子是奇异非混沌吸引子。图3(a)为该奇异非混沌序列的伪随机特性。奇异非混沌序列的伪随机点在确定的区间内均匀分布，如图3(b)所示。同时，奇异非混沌吸引子的存在范围由最大Lyapunov指数λ_x和相位灵敏度指数μ决定，这为奇异非混沌优化算法的参数选择奠定了基础（见图4）。

图2 奇异非混沌吸引子的相图和相敏感函数曲线

Fig. 2 Phase diagram of SNA and plot of phase sensitivity function

图3 奇异非混沌吸引子的时间序列图和点分布图

Fig. 3 Time sequence diagram and point distribution diagram of SNA

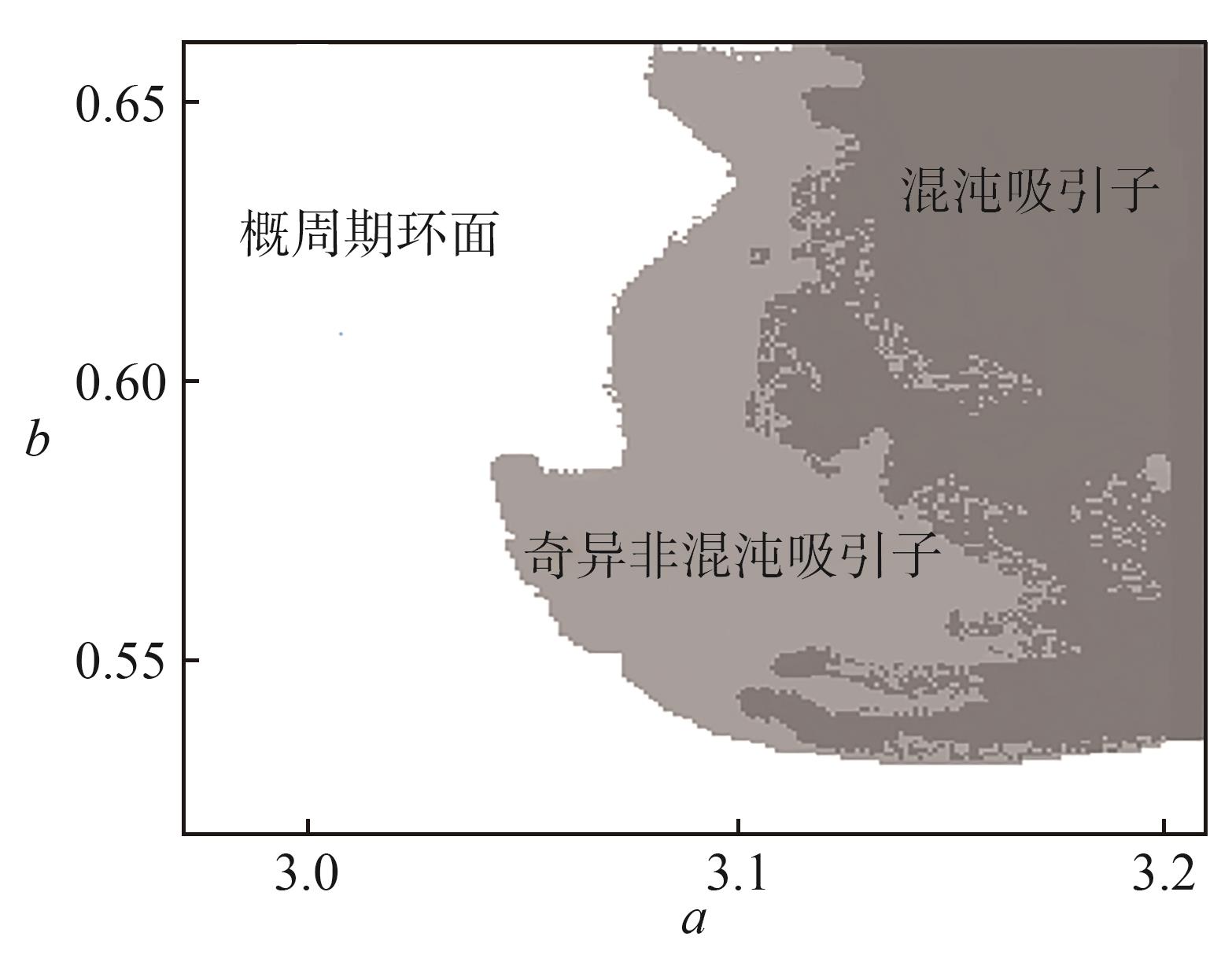
图4 系统(5)在(a-b)平面上的相图

Fig. 4 Phase diagrams for system (5) in the (a-b) plane

1.3　奇异非混沌优化极限学习机

利用奇异非混沌优化算法优化ELM的训练过程中随机产生的输入层与隐含层之间的偏置和权重，在ELM的隐含层神经元数量确定后，其优化过程如下。

（1）初始化奇异非混沌优化算法的参数，包括奇异非混沌系统的参数a、b和均方误差（MSE）的参考值 $\bar{E}$ 等；

（2）对由奇异非混沌系统生成的奇异非混沌序列进行归一化；

（3）奇异非混沌序列用于替换由神经元数量和输入维度确定的N维目标变量（权重和阈值）；

（4）计算损失函数（均方差 $E$ ）；

（5）比较 $\bar{E}$ 和 $E$ 的值，如果 $E$ < $\bar{E}$ ， $\bar{E}$ = $E$ ；其他 $\bar{E}$ = $\bar{E}$ 。

重复步骤（3）~（5）以获得最佳解。

2 改进极限学习机在纸张横幅定量系统解耦中的应用

2.1　应用背景

图5给出了纸张定量控制系统结构图。造纸机扫面架上的定量传感器来回扫描，测得纸张的横幅定量，然后通过调节稀释水流浆箱上的稀释水阀维持定量稳定。单个稀释水水阀的工作会影响周围稀释水阀的控制区域，在控制上表现出强耦合特性。利用稀释水流浆箱本体结构优化解决这种耦合特性造价高昂，且效果有限，因此利用软件解耦相对实用性更高。由于造纸过程中存在的非线性因素和外界干扰，对机器学习的模型及其优化方法要求较高，普通的模型难以取得良好的效果。

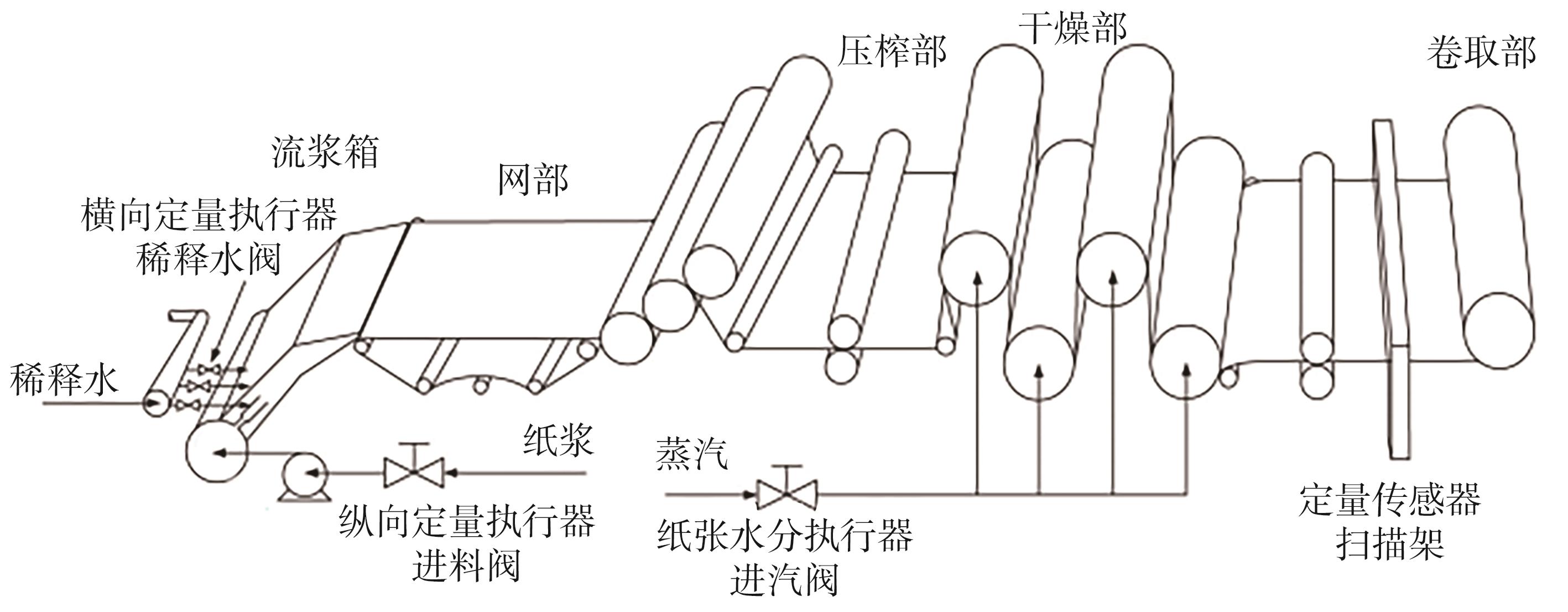
图5 定量控制系统结构

Fig. 5 Structure of basis weight control system

2.2　极限学习机网络解耦

本课题利用文献[

14]中给出的横幅定量系统获取解耦数据。横幅定量系统如式（8）所示。

Y (s) = G_{0} h (s) U (s) + δ (s)

（8）

$Y (s) = [y_{1} (s), y_{2} (s), \dots, y_{n} (s)]$ 是扫面仪测得的实际CD定量输出值， $U (s) = [u_{1} (s), u_{2} (s), \dots, u_{n} (s)]$ 是标准的CD定量设定值。 $G_{0} \in R^{n \cdot n}$ 是降维后的关联矩阵，代表耦合关系。传递函数h(s)为一阶惯性加时滞环节， $δ (s)$ 为外界干扰， $δ (s)$ 是均值为0，标准差为0.16的白噪声。本课题以五输入五输出系统为研究对象，分析了SNOELM解耦方法的优越性。此时设置n=5, G₀=[1, 0.7, 0.3, 0, 0; 0.7, 1, 0.7, 0.3, 0; …; 0, 0, 0.3, 0.7, 1]；h(s)=e^-^s/(2s+1)。此时极限学习机网络设置为五输入五输出，其解耦控制框图如图6所示。其中C₁, …, C₅代表常规PID控制器，V₁, …, V₅为系统G的原始输入，y₁, …, y₅是系统G的原始输出。解耦的目的在于加入ELM网络NN后，整个系统的广义传递函数为5个单回路系统。因此只需保证极限学习机网络解耦器的输入输出为原系统的输入输出的逆，即y₁, …, y₅为ELM网络的输入数据，V₁, …, V₅为ELM网络的输出数据，即可完成解耦。因此取y₁, …, y₅和V₁, …, V₅作为ELM的输入输出进行训练。

图6 ELM解耦框图

Fig. 6 Decoupling block diagram of ELM

通过随机产生的200组数据生成y₁, …, y₅和V₁, …, V₅确定ELM的隐藏层神经元个数；然后利用优化算法得到网络的权值和阈值，得到所需稍微静态ELM解耦器；最后通过50组随机数据验证了基于ELM的解耦算法。

3 算法验证

3.1　算法参数的选择

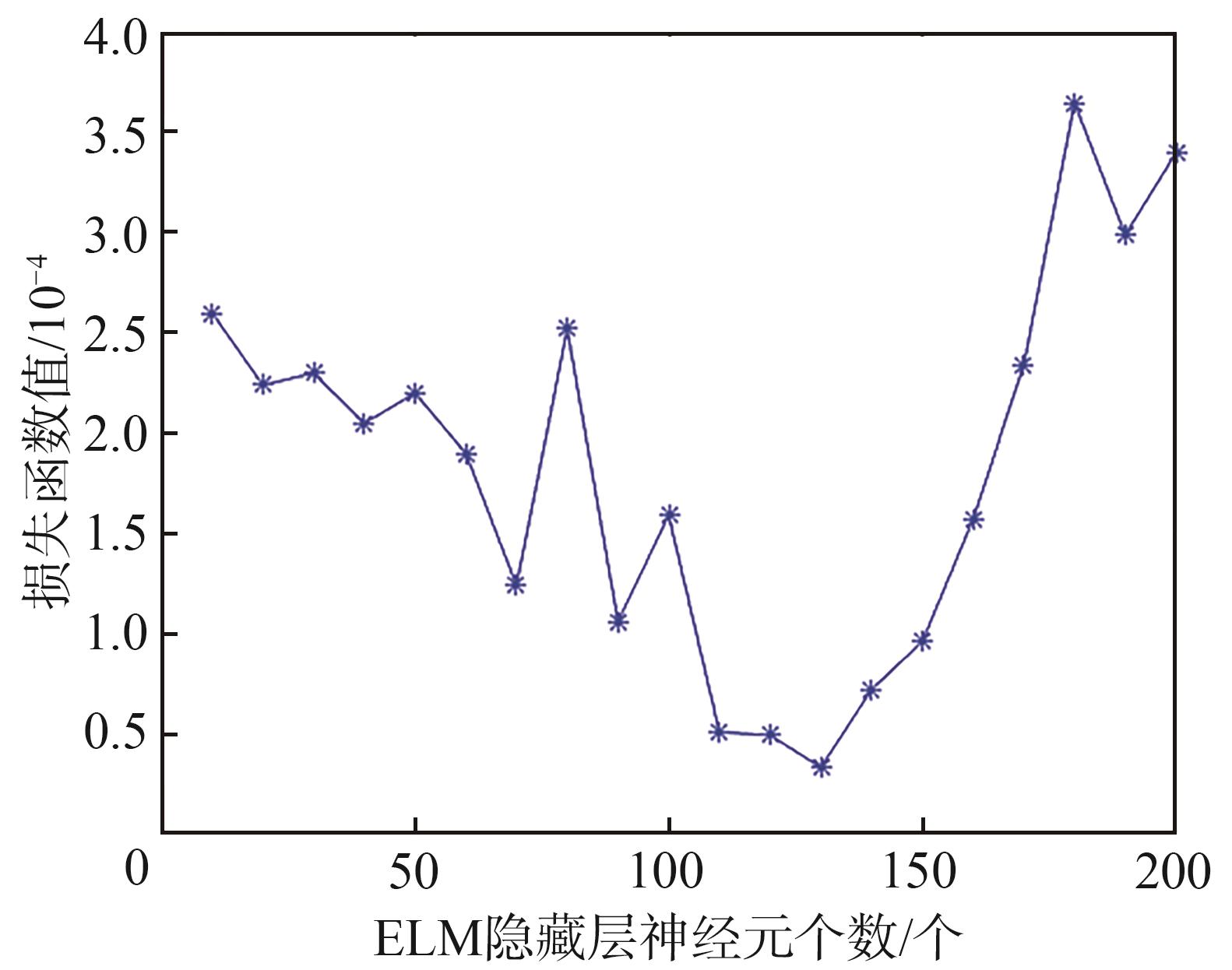
本节利用测试数据确定了最佳ELM的隐藏神经元个数（图7）。由图7可知，ELM在神经元个数达到130个时，损失函数的值趋于最小，当神经元个数超过130个时，出现过拟合，损失函数的值反而增大。因此ELM的隐藏层神经元个数确定为130个。

图7 损失函数随ELM隐藏层神经元个数的变化

Fig. 7 Change of loss function with the number of ELM hidden layer neurons

在PSOELM中，设置种群个数为100，最大迭代次数为40，个体学习率和社会学习率分别为2，最大速度为0.9，惯性系数为0.8。在WOELM中，设置种群个数为100，最大迭代次数为40，a的值从2线性递减到0。在SNOELM中，迭代次数设置为100。

3.2　实验结果

表1为4种ELM解耦器的性能指标。从表1可知，一般ELM存在优化不足和解耦精度低的缺点。然而，SNOELM、WOELM和PSOELM可以克服这些问题。值得注意的是，SNOELM的性能指标（训练时间和性能指标）优于WOELM和PSOELM。

表1 使用ELM、PSOELM、WOELM、SNOELM解耦器的解耦性能

Table 1 Decoupling performance for decoupler using ELM, SNOELM, WOELM, and PSOELM

解耦方法	隐藏层神经元个数/个	训练时间/s	性能指标（MSE）
ELM	130	6.938	3.32×10^-5
PSOELM	130	48.536	5.47×10^-8
WOELM	130	10.354	3.26×10^-8
SNOELM	130	9.262	3.15×10^-8

图8显示了五输入五输出横向定量系统的耦合结果和解耦结果。当输入为[u₁, u₂, u₃, u₄, u₅]=[10, 9, 8, 7, 6]时，耦合输出如图8(a)所示。很明显，输出结果不能满足设定值的要求。图8(b)显示了使用SNOELM的解耦结果，输出结果可以很好地跟踪设定值。为了验证SNOELM的解耦性能，图8(c)显示了将u₁值增加到u₁=12时的解耦结果。很明显，只有输出y₁随设定值u₁的变化而变化，其他输出没有变化。因此，本课题所提出的解耦方法有效。此外，本课题还验证了解耦方法的鲁棒性。图8(d)显示了失配模型h(s)=e^-^s/(2.5s+1)的解耦效果，证明了基于SNOELM的解耦方法具有良好的鲁棒性。

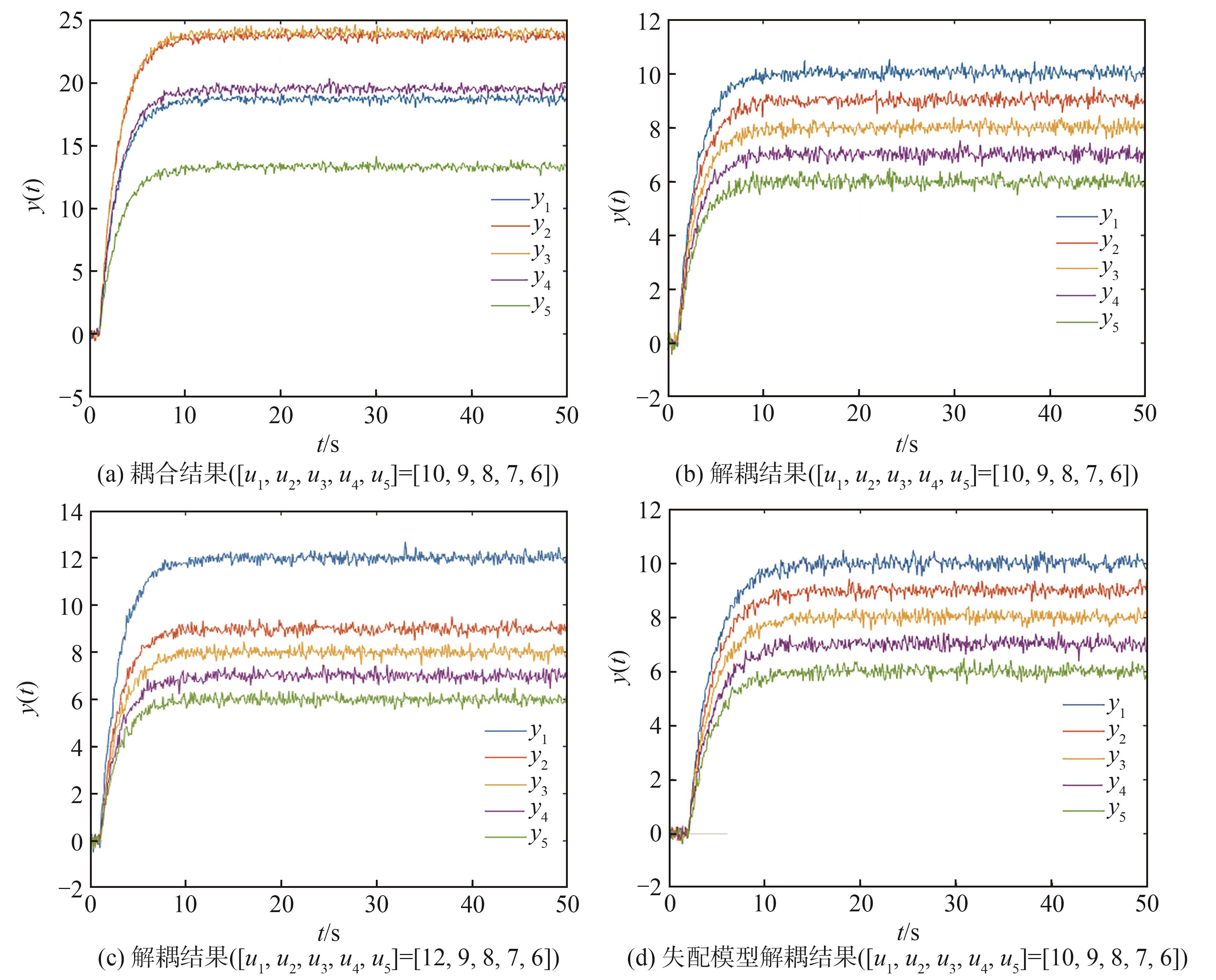
图8 耦合结果和解耦结果

Fig. 8 Results of coupling and decoupling

4 结论

本课题在基于奇异非混沌动力学和极限学习机，提出了一种奇异非混沌优化极限学习机（SNOELM）算法，并将其应用于造纸过程横向定量系统的解耦实验中。实验结果表明，SNOELM比鲸鱼优化极限学习机（WOELM）和粒子群优化极限学习机（PSOELM）具有更短的训练时间和更高的解耦精度；可以同时实现过程比其他算法更加简单，更加适用于造纸过程的横向定量系统的解耦。

参考文献

BAKI H， WANG H， SOYLEMEZ M T， et al. Implementing Machine-directional Basis Weight Control for a Pilot Paper Machine［J］. Control Engineering Practice， 2001， 9： 621-630. [百度学术]

汤伟，王孟效，李明辉，等. 流浆箱先进控制策略及解耦控制算法［J］. 中国造纸学报， 2006， 21（1）： 108-114． [百度学术]

TANG W， WANG M X， LI M H， et al. The Advanced Control Strategies and Decoupling Algorighms of Headbox ［J］. Transactions of China Pulp and Paper， 2006， 21（1）： 108-114. [百度学术]

SHAN W， LIU B. Multidimensional Interpolation Decoupling Strategy for CD Basis Weight of Papermaking Process［J］. Symmetry， DOI： 10.3390/sym12010149. [百度学术]

陈航，汤伟，刘文波，等. 稀释水水力式流浆箱结构与控制［J］. 中国造纸， 2013， 32（12）： 38-44. [百度学术]

CHEN H， TANG W， LIU W B， et al. Structure and Control of a Hydraulic Headbox with Dilution Water［J］. China Pulp & Paper， 2013， 32（12）： 38-44. [百度学术]

宋执环，王慧，吴江. 纸张定量横向分布控制系统的建模与预测控制［J］. 中国造纸学报， 1996， 11（1）： 54-59. [百度学术]

SONG Z H， WANG H， WU J. Cross-direction Basis Weight Profile Modelling and Its Dynamic Matrix Control［J］. Transactions of China Pulp and Paper， 1996， 11（1）： 54-59. [百度学术]

SUN X， LONG C， JIANG H， et al. High-performance Control for a Bearingless Permanent-magnet Synchronous Motor Using Neural Network Inverse Scheme Plus Internal Model Controllers［J］. IEEE Transactions on Industrial Electronics， 2016， 63： 3479-3488. [百度学术]

DONG D， MENG X， FAN L. Decoupling Control of Double-level Dynamic Vacuum System Based on Neural Networks and Prediction Principle［J］. Vacuum， 2011， 86： 218-225. [百度学术]

XIAO C， SUTANTO D， MUTTAQI K M， et al. Online Sequential Extreme Learning Machine Algorithm for Better Predispatch Electricity Price Forecasting Grids［J］. IEEE Transactions on Industry Applications， 2021， 57： 1860-1871. [百度学术]

CHU Z， MA Y， CUI J. Adaptive Reactionless Control Strategy via the PSO-ELM Algorithm for Free-floating Space Robots during Manipulation of Unknown Objects［J］. Nonlinear Dynamics， 2018， 91： 1321-1335. [百度学术]

DONG Z. Extreme Learning Machine based Genetic Algorithm and Its Application in Power System Economic Dispatch［J］. Neurocomputing， 2013， 102： 154-162. [百度学术]

LI L， SUN J， TSENG M， et al. Extreme Learning Machine Optimized by Whale Optimization Algorithm Using Insulated Gate Bipolar Transistor Module Aging Degree Evaluation［J］. Expert Systems with Applications， 2019， 127： 58-67. [百度学术]

SHEN Y， ZHANG Y， JAFARI S. Coexistence of Strange Nonchaotic Attractors in a Quasiperiodically Forced Dynamical Map［J］. International Journal of Bifurcation and Chaos， DOI： 10.1142/S0218127420501837. [百度学术]

SHEN Y， TANG W. Tuning of Two-degree-of-freedom IMC based on a Strange Nonchaotic Optimization Approach for Large Time-delay Processes［J］. Fractals， DOI： 10.1142/s0218348x22500670. [百度学术]

单文娟，汤伟，刘炳. 纸张横幅定量多变量解耦控制策略研究［J］. 中国造纸学报， 2018， 33（4）： 44-50. [百度学术]

SHAN W J， TANG W， LIU B. Multivariable Decoupling Control Strategy for Cross-direction Basis Weight of Papermaking Process［J］. Transactions of China Pulp and Paper， 2018， 33（4）： 44-50. [百度学术]

CPP [百度学术]

优化极限学习机算法及其在纸张横幅定量系统解耦中的应用

摘要

关键词

1 极限学习机及其改进算法

1.1 极限学习机

1.2 奇异非混沌优化

1.3 奇异非混沌优化极限学习机

2 改进极限学习机在纸张横幅定量系统解耦中的应用

2.1 应用背景

2.2 极限学习机网络解耦