网刊加载中。。。

使用Chrome浏览器效果最佳，继续浏览，你可能不会看到最佳的展示效果，

确定继续浏览么?

复制成功，请在其他浏览器进行阅读

芳纶纸撕裂度测量不确定度分析方法的研究

- ORCID：
严瑾
- ORCID：
王雪明
✉
- ORCID：
林晓凤
- ORCID：
杨刚
- ORCID：
刘茜

中航复合材料有限责任公司，复合材料检测技术中心，北京，101300

中图分类号： TS761.2

最近更新：2023-12-21

DOI：10.11980/j.issn.0254-508X.2023.12.007

摘要

本研究根据纸张撕裂度测量的基本要求，对3 mil（厚度0.088 mm）间位芳纶纸进行横向撕裂度测量，对不确定度分量进行分析量化，给出评定方法与步骤，并对芳纶纸横向撕裂度测量不确定度离散区间进行定量评估。结果表明，按置信区间为95%，同一批次5组杜邦T412-3 mil间位芳纶纸撕裂度分别为（3084±24）、（3161±102）、（3092±92）、（3064±134）和（3145±162）mN，覆盖因子k=2，离散区间位于24~162 mN间。按照标准进行符合规范的测量前提下，纸样均匀性引入的不确定度是芳纶纸撕裂度测量不确定度的主要来源；其次是撕裂度仪的校准引入的不确定度；切口长度误差、裁切误差引入的不确定度影响较小；温湿度、试样层数等因素对测量不确定度影响可以忽略。

关键词

芳纶纸; 撕裂度测量; 误差分析; 不确定度

芳纶纸又称聚芳酰胺纤维纸，以其优异的物理性能（高抗张强度、撕裂度、耐磨性等）、良好的耐温性和化学稳定性、优良的阻燃和电绝缘性，广泛应用于国防、航空航天、高速列车、电工绝缘等领域，且市场需求强劲，行业发展前景好^[

1]。

以芳纶纸为原材料，经涂胶、叠合、压制、切割、拉伸、定型、浸胶、固化、切片等工艺制备成的芳纶纸蜂窝芯材是飞机机身次承力结构和舱内结构的重要材料^[

2-3]。因此，航空级芳纶纸蜂窝芯材需具有较高的比强度和比刚度（约为钢的9倍）^{[参考文献 4

百度学术}4]。作为蜂窝芯材的增强体，芳纶纸的机械性能，如撕裂度、抗张强度、断裂伸长率、弹性模量、表面强度等与蜂窝的性能密切相关，因此，对其要求也更为严格^{[参考文献 5

百度学术}5]。根据我国工信部最新发布的《重点新材料首批次应用示范指导目录（2021年版）》，芳纶纸的纵横向撕裂度指标值分别不低于650 mN和1100 mN^{[参考文献 6

百度学术}6]。

对于航空级芳纶纸，其撕裂度可间接影响到后续产品的外观表现及芳纶纸蜂窝的力学性能^[

7-8]，对其他用途的蜂窝芯材同样重要。撕裂度表示纸张抗撕裂的能力。由于撕裂过程中会发生剪应力破坏，且剪应力垂直于裂纹扩展方向，纸张撕裂度是评价纸张抗剪切性能的技术指标^{[参考文献 9

百度学术}9]。此外，撕裂度还与纸张的抗张强度、弹性模量等其他主要机械性能有着极高的关联度，共同影响着芳纶纸蜂窝芯材的力学性能。

由于所取试样不能完全代表该批纸卷，且撕裂度测量结果的准确性通常受仪器测量力值准确性、测量重复性、试样撕裂方向裁切误差和切口长度误差及其他因素（如温湿度、取样层数等）的影响，因此，通过对撕裂度测量不确定度进行评定可判定测量数据的可靠性，增强测量结果之间的可比性，明确不确定度来源，从而减小测量不确定度分量。此外，不确定度评估方法的建立不仅对提高芳纶纸撕裂度检测水平有一定指导意义，也对准确评价航空用芳纶纸的撕裂度等机械性能有一定帮助^[

10-11]。现有文献仅报道了新闻纸、包装纸等撕裂度测量不确定度的评定，缺少对芳纶纸撕裂度测量不确定度分析方法的研究和定量评估。其评定方法存在一定局限性，如忽略了裁切平行度引入的不确定度、有限的测试次数导致测量不确定度评定方法不适用等，均不适用于航空用芳纶纸撕裂度测量不确定度的评定。

本研究通过对杜邦Nomex^® T412-3 mil间位芳纶纸进行不确定度的检测，分析不确定度分量的来源，建立评定方法和步骤，得到不确定度离散区间，从而为准确评估芳纶纸蜂窝用关键原材料的性能提供评价方法和参考依据。

1 实验

1.1　原料及仪器

间位芳纶纸，牌号T412，规格3 mil，厚度0.088 mm，定量65.5 g $/$ m²，杜邦公司。

SLY-S1型撕裂度仪（埃莱门多夫法），济南兰光机电技术有限公司。

1.2　实验方法

1.2.1　试样处理

将芳纶纸卷按GB/T 10739—2002《纸、纸板和纸浆将试样处理和试验的标准大气条件》的要求放置在温度不高于40 ℃，相对湿度10%~35%环境下预处理24 h。取样根据GB/T 450—2008《纸和纸板试样的采取及试样纵横向、正反面的测定》进行，在距纸卷边缘15 mm以外处裁切300 mm×300 mm的纸张若干张，再按照GB/T 10739—2002的要求，悬挂在恒温恒湿实验室中平衡水分4 h以上。实验室环境为温度(23±1) ℃，相对湿度(50±2)%。

1.2.2　试样的测试

依据GB/T 455—2002《纸和纸张撕裂度的测定》，每组测试在同一批次纸卷上取一叠（4层）纸张进行横向撕裂度的测试，沿纸张横向裁切63 mm×50 mm的试样至少40张，以保证1组测试可获得10个有效数据，共测5组。纸张的横向与试样长边平行；对撕裂度仪进行水平、动平衡和静平衡的调节；夹持试样时保证2张正面朝向刀口、2张反面朝向刀口，用冲刀切割20 mm长的预切口，顺着切口撕开，在计算机软件中读取撕裂43 mm试样所需要的力值。

2 测量结果不确定度的评定

2.1　测试方法与评定流程

芳纶纸撕裂度不确定度评定的主要流程见图1。

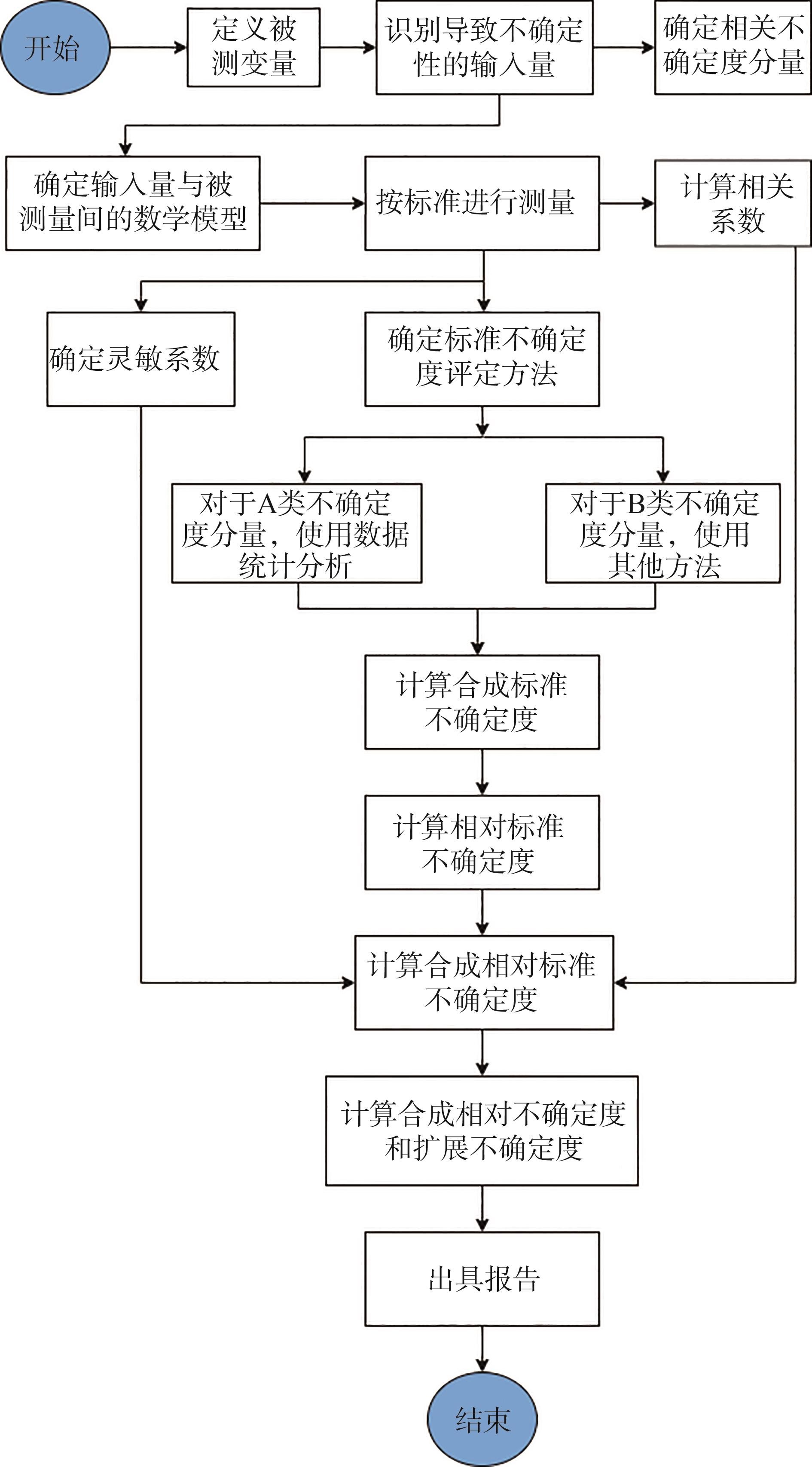
图1 芳纶纸撕裂度不确定度评定流程

Fig. 1 Flow chart for estimation of measurement uncertainty in tearing resistance measurement of aramid paper

2.2　数学模型

在评定不确定度前，根据GB/T 455—2002检测标准的规定建立数学模型，见式（1）。

F = \frac{S \cdot P}{n}

（1）

式中， $F$ 表示撕裂度，mN； $S$ 表示实验方向上的平均刻度读数，mN； $P$ 表示换算因子，即刻度的设计层数，一般为16； $n$ 表示同时撕裂的试样层数，标准规定4层。

2.3　测量不确定度的来源

根据对数学模型和测量步骤的分析，可得芳纶纸撕裂度测量不确定度的来源如下^[

12]。

（1）撕裂度测量引入的不确定度分量，包括撕裂度仪测量力值准确性和测量重复性引入的不确定度分量。

（2）试样撕裂方向裁切误差引入的不确定度分量，包括裁切尺寸误差和裁切平行度误差引入的不确定度分量。

（3）试样切口长度误差引入的不确定度分量。

（4）其他因素引入的不确定度，包括温度和相对湿度、试样均匀性和取样层数等。

2.4　相对标准不确定度的评定

2.4.1　撕裂度测量引入的相对标准不确定度

撕裂度测量引入的标准不确定度主要来源于测量重复性引入的标准不确定度 $u_{1} (\bar{F})$ 和撕裂度仪测量力值准确性引入的标准不确定度 $u_{2} (\bar{F})$ 。

2.4.1.1 $u_{1} (\bar{F})$

测量重复性引入的不确定度为A类不确定度，由重复性实验数据的统计分析得到。依据GB/T 455—2002检测标准，对同一批次T412-3 mil间位芳纶纸的每组撕裂度评定进行10次重复性测试，共测5组，结果见表1，撕裂度平均值 $\bar{F}$ 的计算见式（2）。

表1 撕裂度测量重复性实验结果

Table 1 Repeat test results for trearing resistance

测试次数/次	撕裂度/mN
测试次数/次	第1组	第2组	第3组	第4组	第5组
1	3022	3001	3317	3366	3366
2	3082	3424	2864	2786	3624
3	3110	3186	3210	3065	3004
4	3106	3119	2988	2975	3104
5	3098	2881	3020	3386	3415
6	3054	3241	3151	2969	2885
7	3132	3109	2964	2781	2903
8	3060	3221	3008	3121	3018
9	3082	3340	3253	3220	3145
10	3099	3085	3150	2974	2987
撕裂度平均值 $\bar{F}$ /mN	3084	3161	3092	3064	3145
测量重复性引入的标准不确定度 $u_{1} (\bar{F})$ /mN	10.1	50.0	45.9	67.0	77.5
撕裂度仪测量力值准确性引入的标准不确定度 $u_{2} (\bar{F})$ /mN	0.058	0.289	0.265	0.387	0.447
撕裂度测量引入的合成标准不确定度 $u (\bar{F})$ /mN	10.1	50.0	45.9	67.0	77.5
撕裂度测量引入的相对标准不确定度 $u_{r e l} (\bar{F})$ /%	0.33	1.58	1.48	2.19	2.46

\bar{F} = \frac{1}{n} \sum_{i = 1}^{n} F_{i}

（2）

经计算，每组的 $\bar{F}$ 分别为3084、3161、3092、3064、3145 mN。

单个测量值实验标准偏差S（F）根据贝塞尔公式（式（3）和式（4））计算。

s (F) = \sqrt[]{\frac{1}{n - 1} \sum_{i = 1}^{n} (F_{i} {- \bar{F})}^{2}}

（3）

经计算，每组的 $s (F)$ 分别为32、158、145、212、245 mN。

实验标准偏差计算 $s (\bar{F})$ 如式（4）所示。

s (\bar{F}) = \frac{S (F)}{\sqrt[]{n}}

（4）

经计算，每组的 $s (\bar{F})$ 分别为10.1、50.0、45.9、67.0、77.5 mN。

测量重复性引入的标准不确定度 $u_{1} (\bar{F})$ 计算见式（5）。

u_{1} (\bar{F}) = s (\bar{F})

（5）

经计算，每组的 $u_{1} (\bar{F})$ 分别为10.1、50.0、45.9、67.0、77.5 mN。

2.4.1.2 $u_{2} (\bar{F})$

根据撕裂度仪校准结果可知，撕裂度仪的力值允许误差为 $\pm$ 1.0%，在误差范围内，误差出现的概率各处相同。因此，误差分布满足矩形（均匀）分布^[

13]，取

k

\sqrt[]{3}

，可得撕裂度仪测量力值准确性引入的标准不确定度

u_{2} (\bar{F})

计算见式（6）。

u_{2} (\bar{F}) = \frac{\bar{F} \times 1.0 %}{k} = \frac{\bar{F} \times 1.0 %}{\sqrt[]{3}}

（6）

经计算，每组的 $u_{2} (\bar{F})$ 分别为0.058、0.289、0.265、0.387、0.447 mN。

因此，撕裂度测量引入的合成标准不确定度 $u (\bar{F})$ 计算见式（7）。

u (\bar{F}) = \sqrt[]{u_{1}^{2} (\bar{F}) + u_{2}^{2} (\bar{F})}

（7）

经计算，每组的 $u (\bar{F})$ 分别为10.1、50.0、45.9、67.0、77.5 mN。

因此，撕裂度测量引入的相对标准不确定度 $u_{r e l} (\bar{F})$ 计算见式（8）。

u_{r e l} (\bar{F}) = \frac{u (\bar{F})}{\bar{F}}

（8）

经计算，每组的 $u_{r e l} (\bar{F})$ 分别为0.33%、1.58%、1.48%、2.19%、2.46%。实验结果汇总如表1所示。

2.4.2　试样撕裂方向裁切误差引入的相对标准不确定度 $u_{r e l} (d_{1})$

撕裂方向裁切误差引入的标准不确定度主要来源于撕裂方向裁切尺寸误差引入的标准不确定度 $u_{1} (d_{1})$ 和撕裂方向裁切平行度误差引入的标准不确定度 $u_{2} (d_{1})$ 。

2.4.2.1 u₁(d₁)

试样撕裂方向裁切尺寸误差会影响撕裂度值，引入不确定度。由校准证书可知，裁切尺寸的极限误差为±0.2 mm，在误差范围内，误差出现的概率各处相同。因此，误差分布满足矩形（均匀）分布^[

13]，取

k

\sqrt[]{3}

，则

u_{1} (d_{1})

的计算见式（9）。

u_{1} (d_{1}) = \frac{0.2 m m}{\sqrt[]{3}} = 0.116 m m

（9）

2.4.2.2 u₂(d₁)

试样撕裂方向裁切平行度误差会影响撕裂度值，引入不确定度。由校准证书可知，取样平行度的极限误差为±0.05 mm，在误差范围内，误差出现的概率各处相同。因此，误差分布满足矩形（均匀）分布^[

13]，取

k

\sqrt[]{3}

，则

u_{2} (d_{1})

的计算见式（10）。

u_{2} (d_{1}) = \frac{0.05 m m}{\sqrt[]{3}} = 0.029 m m

（10）

撕裂方向裁切误差引入的合成标准不确定度 $u (d_{1})$ 计算见式（11）。

u (d_{1}) = \sqrt[]{u_{1}^{2} (d_{1}) + u_{2}^{2} (d_{1})} = \sqrt[]{0 . 116^{2} + 0 . 029^{2}} m m = 0.110 m m

（11）

因此，试样撕裂方向裁切误差引入的相对标准不确定度 $u_{r e l} (d_{1})$ 计算见式（12）。

\begin{array}{l} u_{r e l} (d_{1}) = \frac{u (d_{1})}{d_{1}} \times 100 % = \\ \frac{0.110 m m}{63 m m} \times 100 % = 0.17 % \end{array}

（12）

2.4.3　试样切口长度误差引入的相对标准不确定度

撕裂度仪冲刀切口误差会产生试样在撕裂度仪上被切割的切口长度误差，引入撕裂度力值测量的不确定度。由校准证书可知，试样切口长度的极限误差为±0.05 mm，在误差范围内，误差出现的概率各处相同。因此，误差分布满足矩形（均匀）分布^[

13]，取

k

\sqrt[]{3}

，则试样切口长度误差引入的标准不确定度

u (d_{2})

计算见式（13）。

u (d_{2}) = \frac{0.05 m m}{\sqrt[]{3}} = 0.029 m m

（13）

所以，试样切口长度误差引入的相对标准不确定度 $u_{r e l} (d_{2})$ 计算见式（14）。

\begin{array}{l} u_{r e l} (d_{2}) = \frac{u (d_{2})}{d_{2}} \times 100 % = \\ \frac{0.029 m m}{20 m m} \times 100 % = 0.14 % \end{array}

（14）

2.5　标准不确定度分量汇总

根据2.4中对相对标准不确定度评定的结果，可将芳纶纸撕裂度的标准不确定度分量汇总见表2。由表2可以看出，芳纶纸撕裂度的标准不确定度主要由撕裂度的测量引入，而撕裂度测量的标准不确定度主要由测量重复性引入。测量重复性引入的误差主要由实验者的熟练程度和纸张的均匀性决定。对于操作熟练的实验者，重复性的不确定度主要来自纸张的均匀性。综上，在按照标准进行符合规范的测量前提下，芳纶纸撕裂度标准不确定度的大小主要由纸张的均匀性决定。

表2 标准不确定度分量汇总

Table 2 Summary of standard uncertainties

标准不确定度分量	不确定度来源	类型	概率分布	包含因子	标准不确定度	合成标准不确定度	相对标准不确定度
$u (\bar{F})$	$u_{1} (\bar{F})$	A			见表1	见表1	见表1
$u (\bar{F})$	$u_{2} (\bar{F})$	B	矩形	$\sqrt[]{3}$	见表1	见表1	见表1
$u (d_{1})$	$u_{1} (d_{1})$	B	矩形	$\sqrt[]{3}$	0.116 mm	0.110 mm	0.17%
$u (d_{1})$	$u_{2} (d_{1})$	B	矩形	$\sqrt[]{3}$	0.029 mm	0.110 mm	0.17%
$u (d_{2})$	$u (d_{2})$	B	矩形	$\sqrt[]{3}$	0.029 mm		0.14%

2.6　合成相对标准不确定度

因 $u (F)$ 、 $u (d_{1})$ 、 $u (d_{2})$ 测量不确定度分量相互独立，且对于乘积形式模型，灵敏系数均为1，则由式（15）计算芳纶纸撕裂度的合成相对标准不确定度 $u_{c r e l} (F)$ ^[

14]。

u_{c r e l} (F) = \sqrt[]{u_{r e l}^{2} (\bar{F}) + u_{r e l}^{2} (d_{1}) + u_{r e l}^{2} (d_{2})}

（15）

经计算，每组的 $u_{c r e l} (F)$ 分别为0.40%、1.60%、1.50%、2.20%、2.47%。

2.7　合成相对不确定度

由式（16）计算合成相对不确定度 $u_{c} (F)$ 。

u_{c} (F) = \bar{F} \cdot u_{c r e l} (F)

（16）

经计算，每组的 $u_{c} (F)$ 分别为12、51、46、67、81 mN。

2.8　扩展不确定度

依据JJF 1059.1—2012《测量不确定度评定与表示》，为确保给芳纶纸撕裂度测量不确定度有接近95%的置信概率，取包含因子 $k$ =2，得芳纶纸撕裂度测定的扩展不确定度 $U (F)$ 计算见式（17）。

U (F) = k \cdot u_{c} (F)

（17）

经计算，每组的 $U_{c} (F)$ 分别为24、102、92、134、162 mN。

3 测量不确定度结果与讨论

每组撕裂度（F）检测结果平均值为 $\bar{F}$ ，即n=10的撕裂度平均值。 $F$ 检测结果的相对扩展不确定度 $U (F)$ 是由合成标准不确定度 $u_{c} (F)$ 乘以包含因子（ $k$ =2）给出的，可提供约95%的置信概率。按该法测得同一批次5组杜邦T412-3 mil间位芳纶纸撕裂度检测值与扩展不确定度见表3。结果表明，3 mil间位芳纶纸横向撕裂度不确定度离散区间位于24~162 mN。撕裂度测量不确定度主要来源为试样的均匀性，其次为撕裂度仪力值测量准确性引入的不确定度，切口长度误差、裁切误差引入的不确定度影响较小，温湿度、试样层数等因素对测量不确定度影响可以忽略。为了降低芳纶纸测量不确定度，应该从以下4方面考虑：①应在表面平整、厚度均匀且无破损、无污渍的部位取样，减少试样均匀性的影响；②使用高精度的撕裂度仪，降低不确定度；③实验室可以通过及时做好设备的计量、期间核查与维保工作，保证设备测量状态完好；④人员在实验过程中，应严格按照标准操作，降低不确定度。

表3 T412-3 mil芳纶纸横向撕裂度测量结果

Table 3 Test results for the transversal trearing resistance for T412-3 mil aramid paper ( mN )

	第一组	第二组	第三组	第四组	第五组
撕裂度平均值 $\bar{F}$ /mN	3084	3161	3092	3064	3145
合成相对标准不确定度u_crel(F)/%	0.40	1.60	1.50	2.20	2.47
合成相对不确定度u_c(F)/mN	12	51	46	67	81
扩展不确定度U(F)/mN	24	102	92	134	162

4 结论

本研究提出了芳纶纸撕裂度测量不确定度评定流程及分析方法，分析了芳纶纸撕裂度测量不确定度分量的来源，并通过对芳纶纸撕裂度的测量，完成了芳纶纸横向撕裂度测量不确定度的定量评定。

4.1 评定所用数学模型符合GB/T 455—2002《纸和纸张撕裂度的测定》中撕裂度计算方法，精度确高；撕裂度测量结果合格，即符合国家重点新材料首批次应用示范^[

6]要求（不低于1100 mN）与芳纶纸蜂窝原材料入场复验相应指标要求（不低于1505 mN）。

4.2 3 mil间位芳纶纸横向撕裂度不确定度离散区间位于24~162 mN，该值的提出对提高航空用3 mil间位芳纶纸横向撕裂度不确定度定量评定的准确性和可靠性有参考意义。

4.3 芳纶纸撕裂度不确定度主要来源于纸张均匀性引入的不确定度，其次是撕裂度仪测量力值准确性引入的不确定度，切口长度误差、裁切误差引入的不确定度影响较小，温湿度、试样层数等因素对测量不确定度影响可以忽略。

4.4 为了保证撕裂度测试结果的可信度与可比性，需使用高精度的撕裂度仪从而可降低不确定度分量；另外，实验室应及时做好设备的计量、期间核查与维保工作，保证设备测量状态完好。在状态调节、取样、测试中应规范操作，提高准确性。

参考文献

罗玉清，王萌，郝巍，等. 芳纶纸纸基结构性能对蜂窝性能影响关系的研究［J］. 高科技纤维与应用， 2018， 43（5）： 42-47. [百度学术]

LUO Y Q， WANG M， HAO W， et al. Study on Relationships Between Properties of Aramid Paper and Properties of Honeycomb［J］. Hi-Tech Fiber and Application， 2018， 43（5）： 42-47. [百度学术]

胡健，王宜，曾靖山，等. 芳纶纸基复合材料的研究进展［J］. 中国造纸， 2004， 23（1）：49-52. [百度学术]

HU J， WANG Y， ZENG J S， et al. Progress in Development of Aramid Paper［J］. China Pulp & Paper， 2004， 23（1）： 49-52. [百度学术]

李勇. Nomex蜂窝在俄罗斯航空领域的发展及应用［J］. 材料工程， 1995（4）： 3-4. [百度学术]

LI Y. Development and Application of the Nomex Honeycomb in Russia Aerospace Area［J］. Journal of Materials Engineering， 1995 （4）： 3-4. [百度学术]

黄钧铭，孙茂健，朱敏英，等. 蜂窝结构材料用国产芳纶纸性能分析［J］. 高科技纤维与应用， 2008， 33（6）： 33-38. [百度学术]

HUANG J M， SUN M J， ZHU M Y， et al. Performance Analysis of the Domestic Meta-Aramid Paper （PMIA） Used for Honeycomb Structural Material［J］. Hi-Tech Fiber & Application， 2008， 33（6）： 33-38. [百度学术]

刘杰，郝巍，罗玉清，等. 航空用芳纶纸蜂窝性能差异性研究［J］. 失效分析与预防， 2014， 9 （2）： 80-83， 93. [百度学术]

LIU J， HAO W， LUO Y Q， et al. Study on Property Difference of Aviation Aramid Paper Honeycomb［J］. Failure Analysis and Prevention， 2014， 9 （2）： 80-83， 93. [百度学术]

中国工信部. 重点新材料首批次应用示范指导目录（2021年版）［EB/OL］. （2021-12-31）［2023-02-20］. https：//wap.miit.gov.cn/zwgk/zcwj/wjfb/tg/art/2021/art_ba8afb04dc694ad8a5830f15bd5ffda7.html. [百度学术]

Ministry of Inductry and Information Technology of the People’s Republic of China. Guidance Catalog for the First Batch of Application Demonstration of key New Materials （Version 2021）［EB/OL］. （2021-12-31）［2023-02-20］. https：//wap.miit.gov.cn/zwgk/zcwj/wjfb/tg/art/2021/art_ba8afb04dc694ad8a5830f15bd5ffda7.html. [百度学术]

王厚林，王宜，姚运振，等. 芳纶纸蜂窝力学性能与纸张性能相关性的研究［J］. 功能材料， 2013， 44（3）： 349-352. [百度学术]

WANG H L， WANG Y， YAO Y Z， et al. The Relationship between Aramid Paper Honeycomb Mechanical Properties ans Paper Performance［J］. Jorunal of Functional Materials， 2013， 44（3）： 349-352 [百度学术]

宋欢，张明，杨军，等. 航空航天用国产间位芳纶蜂窝纸特性研究［J］.中国造纸， 2022， 41（12）： 24-28. [百度学术]

SONG H， ZHANG M， YANG J， et al. Study on the Properties of Domestic Meta-aramid Honeycomb Paper Used in Aerospace［J］. China Pulp & Paper， 2022， 41（12）： 24-28. [百度学术]

Fan J， Hunter L. Engineering Apparel Fabrics and Garments［M］. Cambridge： Woodhead Publishing， 2009： 161-200. [百度学术]

阚兴传. 食品包装纸撕裂指数测量不确定度的评定［J］. 纸和造纸， 2012， 31（2）： 46-47. [百度学术]

KAN X C. Evaluation of the Uncertainty on Measurement of Tearing Index of Food Packaging Paper［J］. Paper and Paper Making， 2012， 31（2）： 46-47. [百度学术]

范建云. 测量不确定度及其在纸张检测中的应用［J］. 广西轻工业， 2008， 24（5）： 16-17. [百度学术]

FAN J Y. Measurement Uncertainty and Its Applicatin in Paper Test［J］. Guangxi Journal of Light Industry， 2008， 24（5）： 16-17. [百度学术]

张亚娟. 纸张撕裂指数测定不确定度的评定［J］. 计量与测试技术， 2009， 36（5）： 84-85. [百度学术]

ZHANG Y J. The Uncertainty Evaluation for Tearing Index of News Paper［J］. Metrology & Measurement Technique， 2009， 36（5）： 84-85. [百度学术]

杨臣铸. 测量误差基础知识及测量不确定度评定方法（下）［J］. 中国照明电器， 1997（3）： 8-14. [百度学术]

YANG C Z. Basic Knowledge of Measurement Error and Evaluation Method of Measurement Uncertainty （Part Two）［J］. China Light & Lighting， 1997（3）： 8-14. [百度学术]

宋建生. 校准数据处理若干问题研究［J］. 计量技术， 2003（7）： 54-56. [百度学术]

SONG J S. Research on Several Problems of Calibration Data Processing［J］. Metering Technology， 2003（7）： 54-56. [百度学术]

CPP [百度学术]

芳纶纸撕裂度测量不确定度分析方法的研究

摘要

关键词

1 实验

1.1 原料及仪器

1.2 实验方法

2 测量结果不确定度的评定

2.1 测试方法与评定流程

2.2 数学模型

2.3 测量不确定度的来源

2.4 相对标准不确定度的评定

2.5 标准不确定度分量汇总

2.6 合成相对标准不确定度

2.7 合成相对不确定度

2.8 扩展不确定度

3 测量不确定度结果与讨论

4 结论

参 考 文 献

1.1　原料及仪器

1.2　实验方法

2.1　测试方法与评定流程

2.2　数学模型

2.3　测量不确定度的来源

2.4　相对标准不确定度的评定

2.5　标准不确定度分量汇总

2.6　合成相对标准不确定度

2.7　合成相对不确定度

2.8　扩展不确定度

参考文献