网刊加载中。。。

使用Chrome浏览器效果最佳，继续浏览，你可能不会看到最佳的展示效果，

确定继续浏览么?

复制成功，请在其他浏览器进行阅读

基于机器学习的箱纸板质量预测模型构建及比较

- ORCID：
钱继炜 ¹
- ORCID：
李继庚 ¹
- ORCID：
满奕 ^1,2
- ORCID：
洪蒙纳 ^1,3
- ORCID：
何正磊 ¹
✉

1. 华南理工大学制浆造纸工程国家重点实验室，广东广州，510640； 2. 人工智能与数字经济广东省实验室（广州），广东广州，510335； 3. 中新国际联合研究院，广东广州，510555

中图分类号： TS77； TP27

最近更新：2023-07-24

DOI：10.11980/j.issn.0254-508X.2023.07.009

摘要

箱纸板生产涉及一系列复杂工艺流程，且由于缺乏关键质量的在线监测手段，进而导致质量管控困难。为此，本研究尝试基于机器学习方法建立可在线监测箱纸板质量的预测模型，也称软测量模型，以促进上述问题的有效解决。本研究采用箱纸板企业实际数据，训练并比较了随机森林（RF）、梯度提升回归（GBR）、K近邻回归（KNN）及偏最小二乘回归（PLS）在多项质量指标上的预测表现。结果表明，不同质量指标本身很大程度上影响了预测精度的上限，而不同算法对理论上限的逼近程度有显著差异。复杂、非线性的集成模型（RF、GBR）相较于简单模型（KNN、PLS）有更好的表现。

关键词

机器学习; 数据挖掘; 造纸工业; 质量预测; 软测量

不断加剧的市场竞争和日益复杂的生产过程工艺，使得制造业对高效生产管理的需求日趋迫切。因此，现代工厂通过广泛安装物理传感器、分布式控制系统、制造执行系统及相关的生产管理系统以改善生产过程变量的可访问性和可追溯性^[

1-2]，通过监测关键参数以促进该问题的有效解决。

然而，对于造纸工业而言，原纸关键质量变量的获取仍依赖于人工离线检测。该检测方式存在反馈周期长、测试结果不稳定、测试样品覆盖率低等缺陷，严重影响了后续的决策与控制过程。因此，实现对质量变量的实时、在线监测是造纸工业亟需解决的关键问题之一。

受限于现有传感技术和检测手段的发展水平，目前仍不具备可直接在造纸生产过程中对原纸关键质量进行在线测量的工具。而基于易测变量与难测变量之间的交互关系建立预测模型，也称软测量模型，是有效解决上述问题的技术方法，其在相关领域已经得到了广泛的应用与验证^[

3-4]。

针对纸张性能的预测建模方法可大致分为机理建模和数据驱动建模2个大类。机理建模侧重于描述过程的理想状态，针对复杂的现代工业过程，开发完整、准确的机理模型存在极大难度。因此，单独基于机理建立的预测模型较为少见^[

5]。于是，有不少学者在机理研究的基础上应用实验数据，并结合人工经验建立了数学模型，也称为经验模型。其中，最著名的是预测纸张抗张强度的Page模型^{[参考文献 6

百度学术}6]，此外还包括改进的Page模型^{[参考文献 7-8}7-8]及在Page模型基础上建立的耐破度模型^{[参考文献 9

百度学术}9]、撕裂度模型^{[参考文献 10

百度学术}10]等。然而，上述模型的输入涉及纤维性质、相对结合面积、零距抗张强度等本身难以测量的变量，与建立预测模型的初衷相悖。同时，人脑通常无法高效、全面地处理和利用复杂、高耦合、高度非线性的工业数据，导致现有经验模型考虑的输入变量有限且很少与高维的过程变量进行关联，导致其难以应用于实际工业场景^{[参考文献 11

百度学术}11]。

数据驱动的机器学习建模方法凭借能够处理高维、复杂数据并取得良好的预测精度等优点，已经在众多场景中得到广泛研究和应用，是相关研究领域的主要发展趋势。如针对水泥熟料生产过程中高成本、大时延的氧化钙含量化学检测现状提出的卷积神经网络模型^[

12]；用于监测城市污水化学需氧量的混合卷积神经网络和长短神经记忆网络模型^{[参考文献 13

百度学术}13]；用于监测流量的改进K近邻模型^{[参考文献 14

百度学术}14]；用于预测造纸废水出水指标的随机森林模型^{[参考文献 15

百度学术}15]、相关向量机模型^{[参考文献 16

百度学术}16]以及人工神经网络模型^{[参考文献 17

百度学术}17]等。针对造纸工业的原纸质量预测建模研究而言，目前主要包括应用于瓦楞原纸的支持向量回归模型^{[参考文献 18

百度学术}18]和偏最小二乘模型^{[参考文献 19

百度学术}19]；应用于生活用纸的梯度提升回归模型等。然而，现有的大多数研究仅侧重于模型选择，并未根据建模对象和数据特征对整体的建模流程进行详细可行的设计。此外，作为最重要的工业用纸品种之一，目前关于箱纸板质量的预测研究仍为空白，而工业用纸生产企业对箱纸板质量指标（平滑度、耐折度、耐破度等）的在线监测需求极为迫切。

因此，本研究将针对箱纸板的平滑度、耐折度和耐破度进行详细的预测建模研究。首先通过有监督的方式对建模数据集进行划分，并结合特征机理，引入新特征作为模型共同输入。然后，对不同质量指标分别建立多种基于机器学习的质量模型，包括随机森林（random forest, RF）、梯度提升（gradient boosting regression, GBR）、K近邻回归（K-nearest neighbor, KNN）以及偏最小二乘（partial least squares regression, PLS），并利用网格搜索结合遗传算法的参数优化框架，对模型超参数进行调优。最后采用判定系数（coefficient of determination,R²）、均方根误差（root mean square error, RMSE）、平均绝对百分比误差（mean absolute percentage error, MAPE）评价模型预测表现并进行比较与分析。

1 建模数据整理

1.1　原始数据采集和预处理

本研究的数据源自安徽某造纸厂2021年5月至2021年11月的生产过程数据和质量检测数据。采集的原始特征共计24个维度，其中包括21维过程变量和3维质量变量，相关变量的具体情况分别如表1和表2所示。

表1 数据集的过程变量

Table 1 Process variables of the dataset

符号	含义	单位
P_w1	第一道湿压榨中2个压榨棍之间的线压力	kN/m
P_w2	第二道湿压榨中2个压榨辊之间的线压力	kN/m
P_cal	压光部2个压光辊之间的线压力	kN/m
BW	单位面积纸张的质量，即定量	g/m²
BW_a	单位面积纸张的绝干质量，即绝干定量	g/m²
W_us	单位面积纸张上表面施胶量	g/m²
W_ls	单位面积纸张下表面施胶量	g/m²
M_t1	面层干强剂质量流量	kg/min
M_b1	底层干强剂质量流量	kg/min
M_t2	面层助留剂质量流量	kg/min
M_b2	底层助留剂质量流量	kg/min
M_t3	面层填料质量流量	kg/min
M_b3	底层填料质量流量	kg/min
F_cal	压光过程中纸幅的张力	kN/m
F_cur	卷曲过程中纸幅的张力	kN/m
v_gap	浆速和网速的差值	m/min
v_ratio	浆速和网速的比值
T_cal	压光辊表面实际温度	℃
T_wind	施胶剂热风温度	℃
R	水分含量	%
h	纸幅厚度	mm

表2 数据集的质量变量

Table 2 Quality variables of the dataset

符号	含义	单位
S	平滑度	s
R_f	耐折度	次
F_b	耐破度	kPa

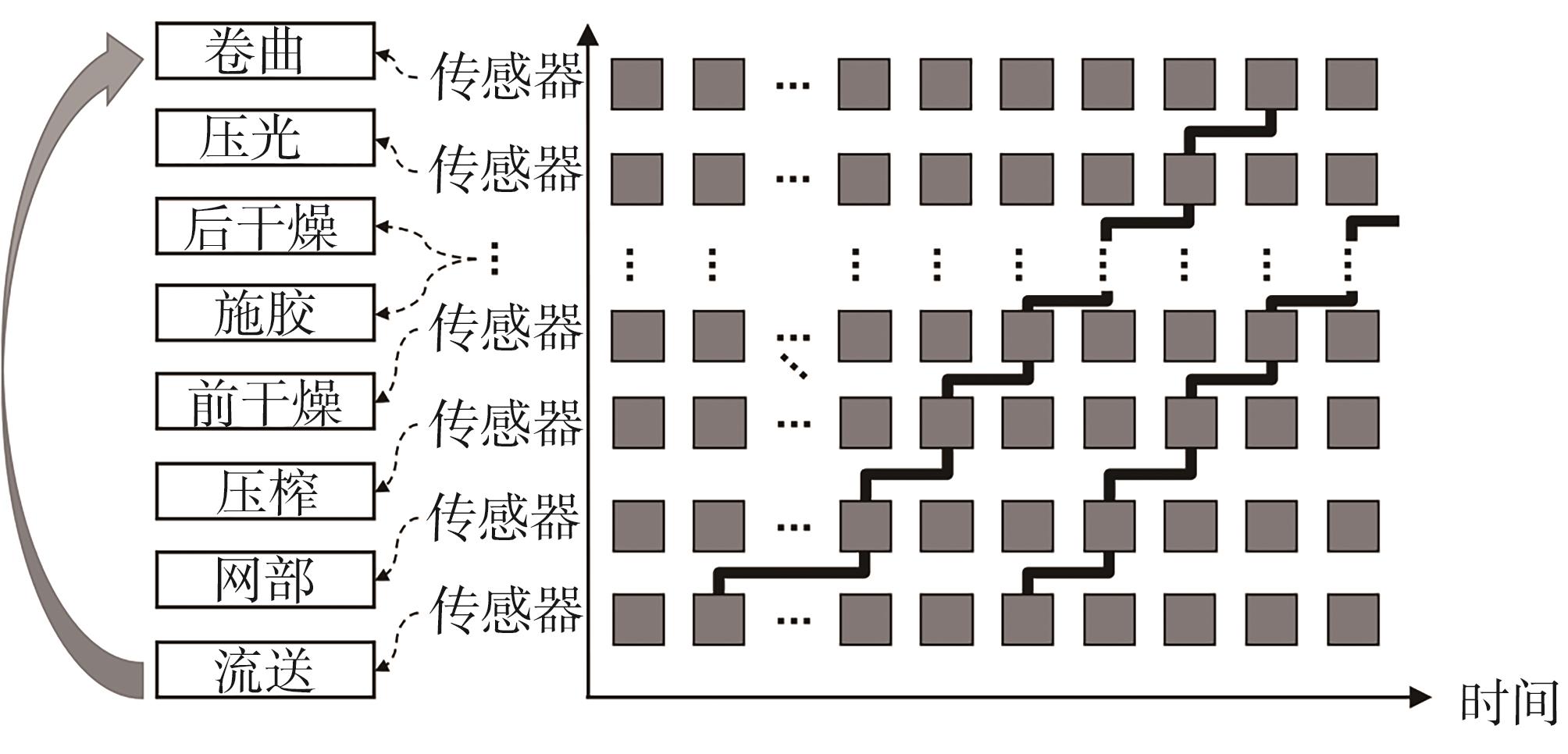
由于上述过程变量主要通过在线传感器实时采集获取，而不同传感器的采样频率、位置和时间点有较大差异，因此，不同数据间需围绕时间刻度进行匹配。本研究采用了步长与宽度相同的滑动窗口（均为每分钟），在时间尺度上处理不规整的颗粒度异化数据，以获得时间和频率规整的实验数据集，为后续数据挖掘提供便利。考虑到测试纸样在造纸过程中经过不同传感器的先后位置顺序，生产过程数据之间的理论匹配情况如图1中黑色实线所示。但对于本研究而言，分析对象采用的纸机属于现代高速夹网纸机，浆料从流浆箱喷浆上网、成形、压榨、干燥直至纸机末端卷曲约在1 min内即可完成，再考虑到传感器频率、读数精度等问题，因此，视完成颗粒度转换后的过程变量已经在时间戳上进行了对齐。

图1 过程数据匹配示意图

Fig. 1 Schematic representation of process data matching

此外，由于箱纸板质量变量（即平滑度、耐折度和耐破度）主要通过离线检测的方式获取，且检测频率以卷轴为单位并通常有多次测试结果。因此，上述2个部分数据将通过母卷下卷时间进行匹配^[

20]，且对多次测试的结果做了均值处理。针对匹配完成后的原始数据，本研究进一步采用了拉依达准则清除异常样本。最后共计获得972组有效的实验数据集。完整的原始数据处理技术路线图如图2所示。

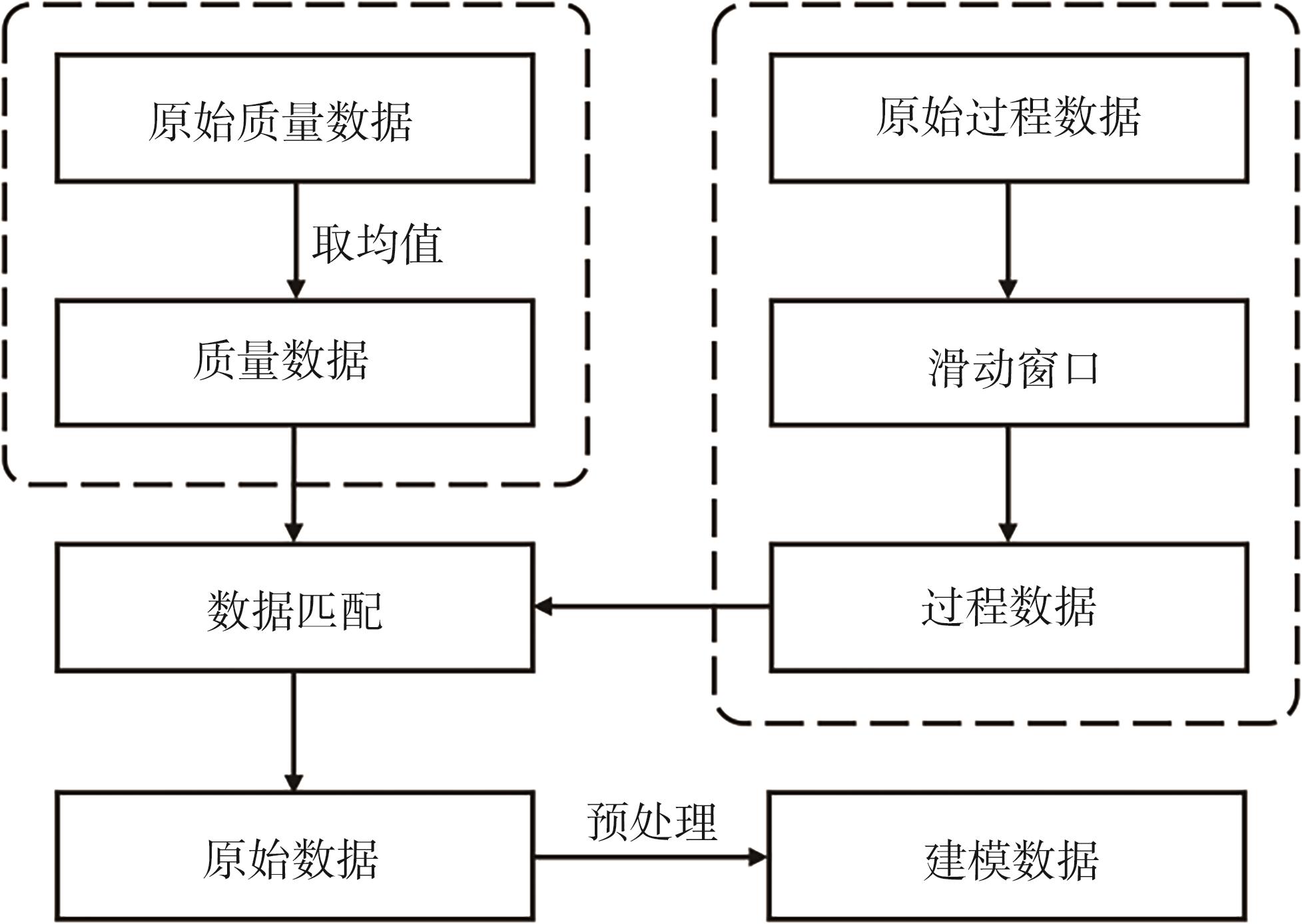
图2 原始数据处理技术路线图

Fig. 2 Technical route of raw data processing

1.2　测试和训练数据划分

纸张定量作为造纸过程最重要的控制指标，其通常可作为工况划分的依据。考虑到不同产品定量下的过程数据可能存在局部特性，且结合数据集在定量划分上表现出的显著聚类倾向。本研究在划分训练数据和测试数据时并未采取常规建模研究中对整个数据集进行随机划分的训练方式。为了确保模型的稳定性和全局性，本研究在数据划分过程中主要结合了相关研究提出的聚类划分^[

21]及局部建模^{[参考文献 22

百度学术}22]等思想，采用了如图3所示的训练与测试集的划分方法。首先，根据定量将数据样本空间进行有监督划分，共计划分得到6个子空间。然后，从各个样本空间随机选取相同数量的样本（35个样本），汇总成最终的测试数据集，而剩余部分则汇总为训练数据。其中，在各样本空间选取相同数量样本的原因主要包括以下两点：第一，各样本空间的数据量差异由数据采集导致，而数据本身在实际工业环境中则等效；第二，后续使用的模型评价指标（如R₂、RMSE等）均包含取均值思想。因此，相同数量的测试样本可以确保各样本空间的数据对最终评价指标的影响相同。最终的训练集和测试集样本比例约为3.6∶1。

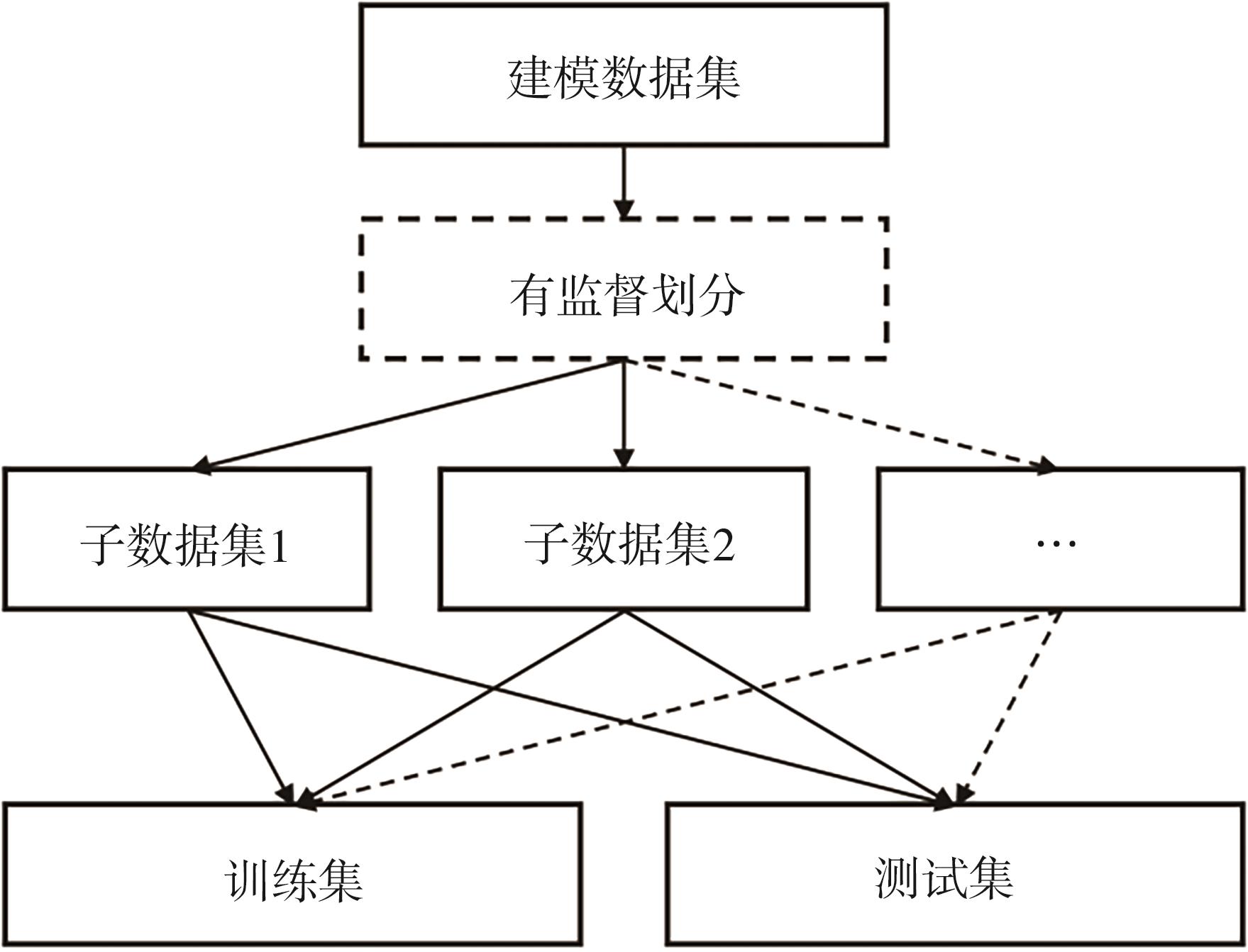
图3 训练与测试集的划分方法

Fig. 3 The method of dividing the training and test data

1.3　特征生成与特征选择

在造纸生产过程中，各类化学品的使用会对最终产品的质量产生直接影响，且在实际生产中，调控化学品的添加量是生产动态过程中最常见、最有效的管理手段。为此，本研究将以各类化学品消耗作为主要切入点，生成新的特征变量。根据表1可知，所采集的原始数据中与造纸化学品有关的原始特征包括M_t1、M_b1、M_t2、M_b2、M_t3、M_b3、W_us、W_ls。考虑到上网纸幅（研究对象）是两面强制脱水，在流送系统中加入的造纸化学品会在流浆箱喷浆上网和网部大量脱水过程中形成湍流混合，且其面层与底层、上表面和下表面的造纸化学品用量本身差异不大。于是，本研究分别生成了干强剂总流量、助留剂总流量、填料总流量以及施胶总流量4个新的特征变量。在前3个广度量特征的基础上与定量计算商数，进一步生成了3个强度量特征，即可分别用于表征吨纸干强剂消耗量的x₁（干强剂总流量/定量）、表征吨纸助留剂消耗量的x₂（助留剂总流量/定量）、表征吨纸填料消耗量的x₃（填料总流量/定量）。假设各类造纸化学品的留着率、配制的质量浓度及纸机车速等均保持稳定，则三者的特征归一化结果与实际各类造纸化学品吨纸消耗量的归一化结果一致。

同时，本研究通过相关系数矩阵（如图4所示）和专家经验来处理冗余变量，如利用Pearson相关系数法明确BW与BW_a的相关性极高，于是结合专家经验最终保留前者。此外还包括v_gap和v_ratio、新生成的特征和对应的原始特征等。最终，在充分考虑模型的物理含义、相关系数矩阵、特征可解释性等因素后，确定建模的输入变量如表3所示。

图4 Pearson相关系数矩阵

Fig. 4 Pearson correlation coefficient matrix

表3 建模使用的输入变量

Table 3 Inputted variables for modeling

符号	含义	单位
P_w1	第一道湿压榨中2个压榨棍之间的线压力	kN/m
P_w2	第二道湿压榨中2个压榨辊之间的线压力	kN/m
P_cal	压光部2个压光辊之间的线压力	kN/m
BW	单位面积纸张的质量，即定量	g/m²
F_cal	压光过程中纸幅的张力	kN/m
v_ratio	浆速和网速的比值
a_ts	单位面积纸张的总施胶量	g/m²
x₁	干强剂总质量流量/ 纸张定量	10³m²/min
x₂	助留剂总质量流量/ 纸张定量	10³m²/min
x₃	填料总质量流量/ 纸张定量	10³m²/min

2 建模与验证

2.1　机器学习算法与参数优化方法

本研究采用的模型方法包括2种基于不同思想的集成学习（分别为RF^[

23]和GBR^{[参考文献 24

百度学术}24]）、KNN^{[参考文献 25

百度学术}25]和PLS^{[参考文献 26

百度学术}26]。

为了对模型超参数进行寻优，本研究尝试结合了网格搜索^[

27]（grid search, GS）和启发式算法^{[参考文献 28-29}28-29]等广泛应用于模型超参数调化的实用方法。GS属于暴力求解算法，可以有效杜绝超参数寻优过程陷入局部最优，然而在面对参数较多、网格参数颗粒度较细等情况时，模型的训练过程非常耗时。与之相反，遗传算法（genetic algorithm，GA）则属于启发式算法，有着较强的局部搜索能力，在求解复杂问题时也能实现快速收敛。因此，本研究提出了结合2种算法优势的超参数优化框架，并通过交叉验证确定各模型的最佳超参数，优化过程及具体结构如图5所示。该方法首先利用合理设置的GS求解超参数的次优解，在此基础上生成缩小范围后的参数空间。然后，利用GA的局部搜索能力确定超参数的最优取值。本研究考虑的随机森林回归超参数包括弱学习器个数、最大深度、叶子节点最小样本数、节点划分最小样本数；梯度提升回归超参数包括弱学习器个数、最大深度、学习率、叶子节点最小样本数、节点划分最小样本数；K近邻回归超参数包括近邻数量、距离权重；偏最小二乘回归超参数包括保留主成分数。

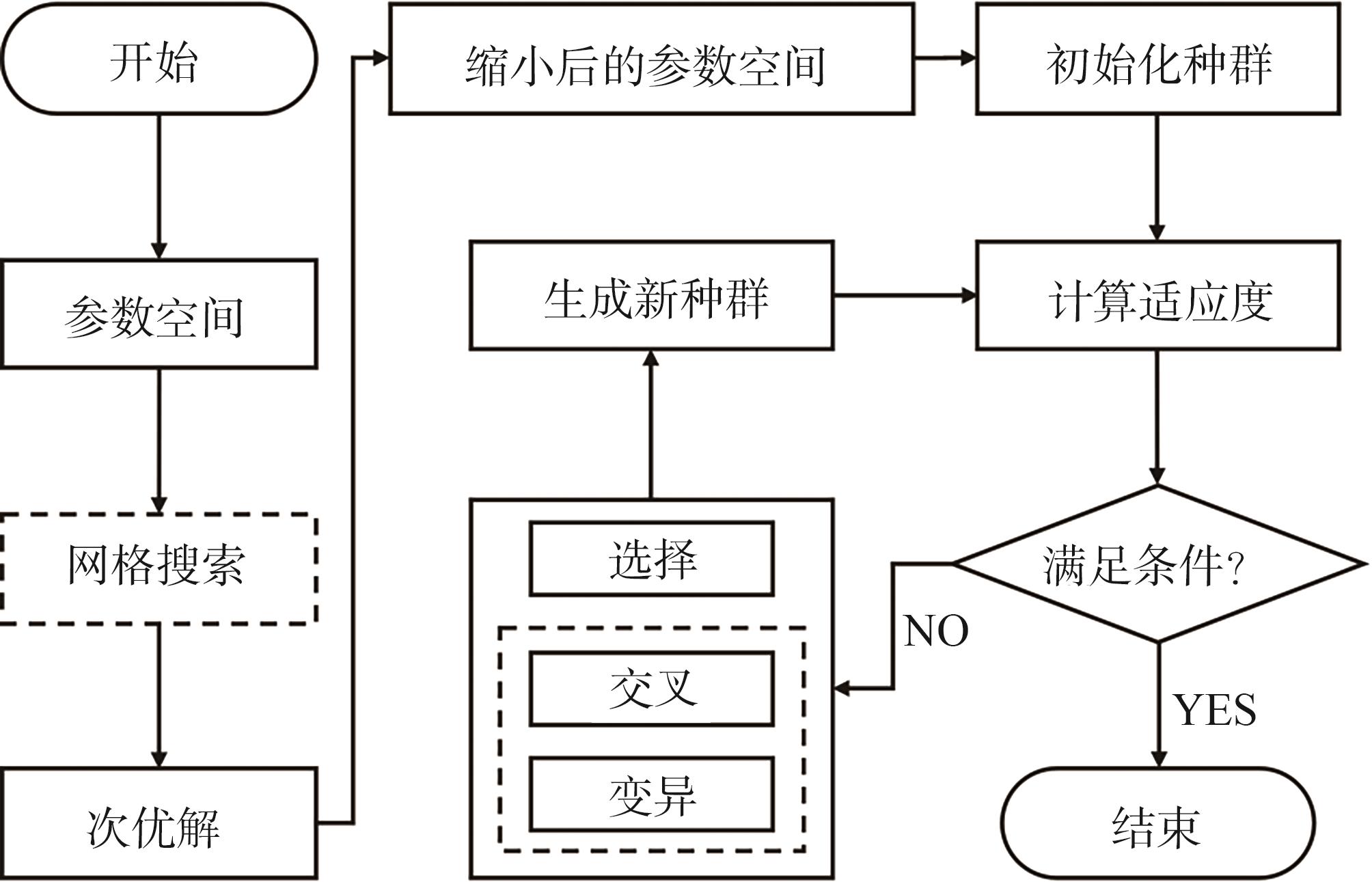
图5 网格搜索结合遗传算法的调参框架

Fig. 5 Framework for grid search combined with genetic algorithm

2.2　模型评价指标

针对预测模型的表现，本研究将使用判定系数（R²）、均方根误差（RMSE）及平均绝对百分比误差（MAPE）作为回归性能的评价指标，从拟合程度、归一化误差以及相同数量级下误差这3方面综合比较不同算法的优劣。相关评价指标的具体计算表达式分别如式(1)~式(3)所示。

R^{2} = 1 - \frac{\sum_{i = 1}^{n} {(y_{i} - {\hat{y}}_{i})}^{2}}{\sum_{i = 1}^{n} {(y_{i} - \bar{y})}^{2}}

（1）

R M S E = \sqrt[]{\frac{1}{n} \cdot \sum_{i = 1}^{n} {(y_{i} - {\hat{y}}_{i})}^{2}}

（2）

M A P E = \frac{\sum_{i = 1}^{n} |(y_{i} - {\hat{y}}_{i}) ∕ y_{i}|}{n} \times 100 %

（3）

式中， $n$ 表示测试样本的数量； $y_{i}$ 表示测试样本 $i$ 的取值； ${\hat{y}}_{i}$ 和 $\bar{y}$ 分别表示预测值和所有预测值的均值。

3 结果与分析

不同机器学习算法分别预测各项质量指标的具体结果如表4所示。从表4可以发现，RF、GBR、KNN在耐破度指标上均有良好表现，且R²均超过0.98，MAPE均小于3%。其原因可能是耐破度与建模输入的特征之间有较好的相关性。而对于平滑度和耐折度而言，任一模型的表现均有所下降。这说明预测目标本身在很大程度上影响了机器学习模型的预测表现上限。

表4 不同机器学习算法的预测表现

Table 4 Prediction performance of different machine learning algorithm

	RF			GBR			KNN			PLS
	R²	RMSE	MAPE/%	R²	RMSE	MAPE/%	R²	RMSE	MAPE/%	R²	RMSE	MAPE/%
S	0.849	0.608	4.62	0.851	0.605	4.55	0.820	0.665	4.95	0.769	0.752	6.01
R_f	0.838	0.333	2.94	0.818	0.353	3.17	0.784	0.385	3.22	0.682	0.467	4.23
F_b	0.994	3.560	1.54	0.993	3.632	1.57	0.992	3.978	1.83	0.989	4.883	2.31

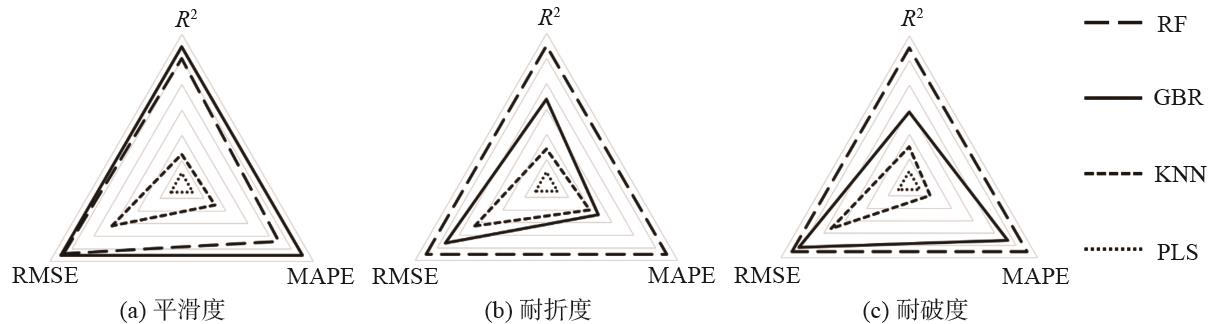
为了更直观地展示不同机器学习算法在不同质量指标上的表现差异，本研究在原有评价指标的数值基础上进行了计算倒数、归一化等处理，并根据处理后的数值绘制了如图6所示的评价指标的雷达图。雷达图中三角形面积的大小反映了模型的表现优劣，即三角形面积越大则表明对应模型效果越好。其中，三角形的各方向则对应模型在不同的评价指标上的具体表现。

图6 评价指标的雷达图

Fig. 6 Radar chart of evaluation indicators

从图6可以发现，集成模型（RF、GBR）在3个预测目标上的表现均优于简单模型（KNN、PLS）。在平滑度指标上，GBR的表现最佳；在耐折度和耐破度指标上，RF的表现最佳。集成学习模型相较于简单模型在R²上可提升0.001~0.156，MAPE上可提升0.05%~1.46%。简单模型表现较差的原因可能是其在处理高维、复杂问题时的天然劣势，即拟合程度不足。然而，模型在实际应用时难免受工况迁移、数据漂移等影响需要对超参数进行调整。简单模型相较于集成学习有更短的训练时间，在满足精度要求的情况下可能会是更好的选择。此外，PLS的表现不及另外3个模型，原因可能有以下两方面：第一，本研究考虑的4个模型中只有PLS属于线性模型，而线性模型通常难以解决非线性问题；第二，RF、GBR和KNN的算法机理均包含样本再划分或再选择的过程，可使三者受训练样本不平衡的影响较小，而PLS可能受多数样本的取值影响，导致在少数样本上的表现不佳。

图7给出了不同模型在20个测试样本上的质量指标预测值和实际值结果。通过观察图7可以发现，RF、GBR、KNN对于同一样本的同一质量指标具有相似的预测结果倾向。如图7(a)中的样本3、6、7、8、9、10、11、12、14等的预测值相近且相较于实际值均偏小（或偏大），相似的情况还出现在图7(b)中的样本1、3、8、19，以及图7(c)中的样本10、20等。此处将主要结合KNN算法的机理尝试给出可行的解释。KNN是一种关注数据局部特点的机器学习算法，其测试样本的预测值实际上是训练集中与该测试样本最相关的若干个训练样本实际值的加权平均。因此，KNN的输出结果很大程度上取决于训练样本的空间分布情况和最相关样本的判断依据。同时，集成学习（RF、GBR）的基本组成是决策树，后者包含了根据特定规则划分数据的机制。所以，训练数据和测试数据的划分可能是RF、GBR、KNN出现相似预测结果倾向的共同原因。这也侧面说明了数据集划分对预测建模的重要性，其很大程度上决定了模型的表现。因此，为了确保建立的模型能够客观反映其实际应用于工业场景时的预测表现，即模型评价不失真，需要对数据集划分阶段进行更多合理的设计。PLS也表现出相似的预测趋势，但是存在细微区别。如图7(a)中的样本2、9、20等，虽然4个模型的预测值均小于实际值，但PLS预测值和实际值的偏离程度远高于RF、GBR和KNN。相似的情况还出现在图7(b)中的样本4、5、9、13、17，图7(c)中的样本4、11、13等，原因可能是线性的PLS对离群点更加敏感，导致其对个别离群样本的预测表现较差。

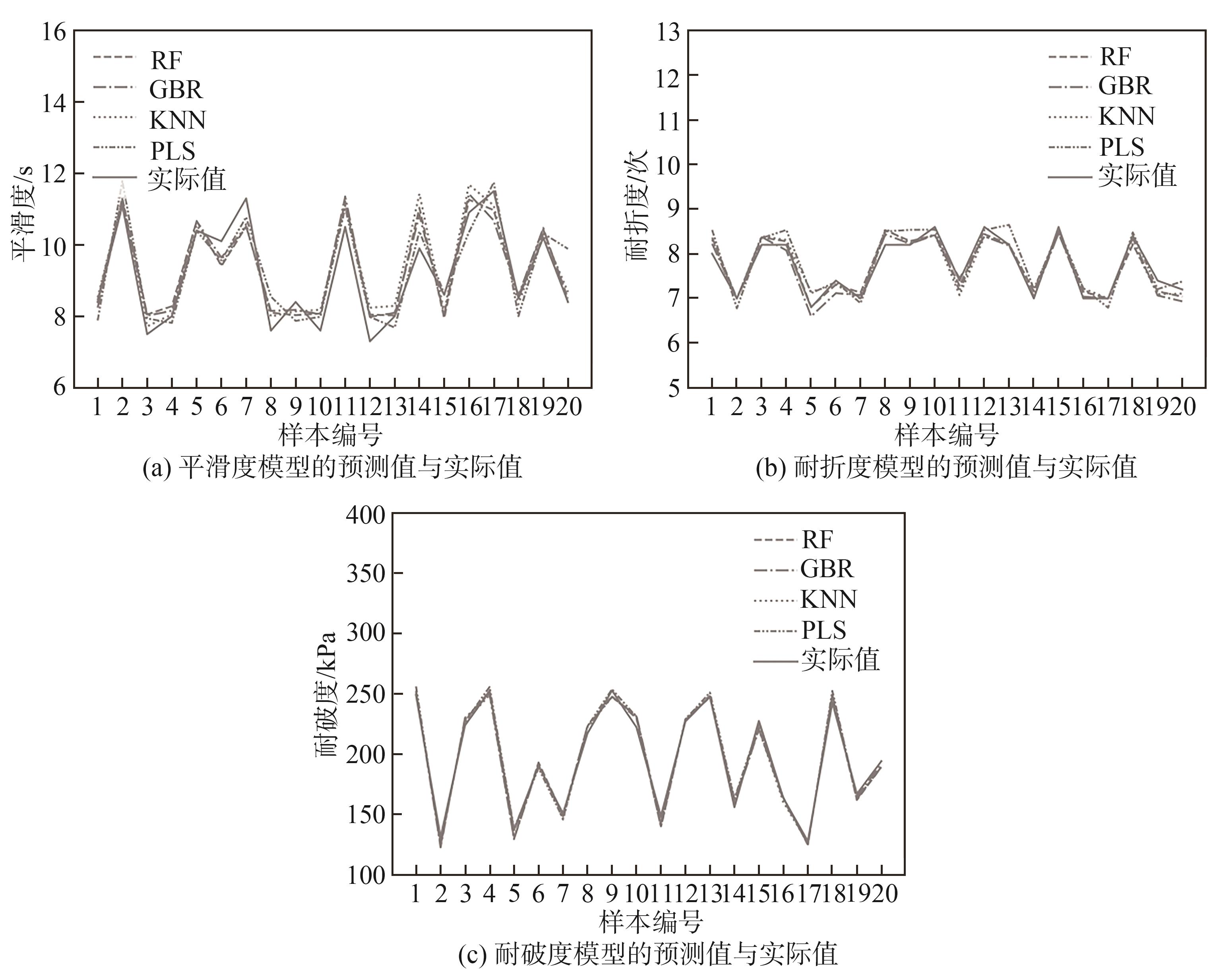
图7 不同机器学习算法在3项质量指标上的拟合结果

Fig. 7 Fitting results of different machine learning algorithm on three quality indicators

4 结论

开发质量预测模型是监测现代工业中关键变量的有效方法。针对箱纸板关键变量获取频率低、结果不准确、反馈滞后等现状，本研究对其关键变量（包括平滑度、耐折度和耐破度）进行了详细的建模研究。具体而言，本研究采用了步长和宽度相同的滑动窗口在时间尺度上处理原始过程数据；根据下卷时间将过程数据与质量数据进行匹配；采取有监督方法对数据集进行划分；结合过程机理生成了可解释性更强的新特征共同作为模型的输入；最后比较了随机森林、梯度提升、K近邻回归、偏最小二乘算法在不同质量指标上的预测表现。

结果表明，上述4种机器学习算法在耐破度指标上的预测表现相近，且远好于在平滑度和耐折度上的表现。然而，针对同一质量指标而言，不同算法间存在较大差异。其中，集成模型相较简单模型能取得更好的预测表现。同时还发现，不同算法对同一样本的同一质量指标有着相似的预测结果倾向，侧面反映了质量预测建模研究不仅需要考虑模型类型，还需要考虑数据集划分以确保离线模型的表现不失真。此外，模型在实际应用于工业环境前，仍需要对超参数进行调整。简单模型相较于复杂模型虽然在预测精度表现上相对较差，但能够节省大量训练时间，在允许的误差范围内，其应用可能更加广泛。

参考文献

Man Y， Hong M N， Li J G， et al. Paper Mills Integrated Gasification Combined Cycle Process with High Energy Efficiency for Cleaner Production［J］. Journal of Cleaner Production， 2017， 156： 244-252. [百度学术]

Chen X B， Man Y， Zheng Q F， et al. Industrial Verification of Energy Saving for the Single-tier Cylinder Based Paper Drying Process［J］. Energy， 2019， 170： 261-272. [百度学术]

于静江，周春晖. 过程控制中的软测量技术［J］. 控制理论与应用， 1996， 13（2）： 137-144. [百度学术]

YU J J， ZHOU C H. Soft Measurement Techniques in Process Control［J］. Control Theory and Technology， 1996， 13（2）： 137-144. [百度学术]

Sun Q， Ge Z. A Survey on Deep Learning for Data-driven Soft Sensors［J］. IEEE Transactions on Industrial Informatics， 2021， 17（9）： 5853-5866. [百度学术]

Kadlec P， Gabrys B， Strandt S. Data-driven Soft Sensors in the Process Industry［J］. Computers & Chemical Engineering， 2009， 33（4）： 795-814. [百度学术]

Page D H. A Theory for the Tensile Strength of Paper［J］. Tappi Journal， 1969， 52： 674-681. [百度学术]

陶劲松，刘焕彬，陈小泉，等. 纸页水分含量对纤维相对结合面积和剪切抗张强度的影响［J］. 造纸科学与技术， 2007（2）： 1-5. [百度学术]

TAO J S， LIU H B， CHEN X Q， et al. Influence of Moisture Content of Paper Sheet on Relative Fiber Binding Area and Shear Tensile Strength［J］. Paper Science & Technology， 2007（2）： 1-5. [百度学术]

陶劲松，刘焕彬. 基于过程抄造参数的纸页抗张强度预测模型的研究［J］. 应用基础与工程科学学报， 2010， 18（S1）： 41-51. [百度学术]

TAO J S， LIU H B. Research on the Prediction Model of Sheet Tensile Strength Based on Process Copying Parameters［J］. Journal of Basic Science and Engineering， 2010， 18（S1）： 41-51. [百度学术]

El-Hosseiny F， Anderson D. Effect of Fiber Length and Coarseness on the Burst Strength of Paper［J］. Tappi Journal， 1999， 82（1）： 202-203. [百度学术]

Gates D J， Westcott M. On the Work to Pull Out Fibers via Bond Breakage During Paper Tearing［J］. Journal of Pulp and Paper Science， 2001， 27（11）： 369-372. [百度学术]

李远华，刘焕彬，陶劲松，等. 纸张抗张强度模型的研究进展［J］. 中国造纸， 2014， 33（1）： 65-69. [百度学术]

LI Y H， LIU H B， TAO J S， et al. Research Progress of Paper Tensile Strength Model［J］. China Pulp & Paper， 2014， 33（1）： 65-69. [百度学术]

Jiang X， Ge Z. Augmented Multidimensional Convolutional Neural Network for Industrial Soft Sensing［J］. IEEE Transactions on Instrumentation and Measurement， 2021， 70： 1-10. [百度学术]

Wang Z F， Man Y， Hu Y S， et al. A Deep Learning Based Dynamic COD Prediction Model for Urban Sewage［J］. Environmental Science： Water Research & Technology， 2019， 5（12）： 2210-2218. [百度学术]

Cheng T， Harrou F， Sun Y， et al. Monitoring Influent Measurements at Water Resource Recovery Facility Using Data-driven Soft Sensor Approach［J］. IEEE Sensors Journal， 2018， 19（1）： 342-352. [百度学术]

辛辰，刘鸿斌. 预测造纸废水出水指标的随机森林建模方法［J］. 中国造纸， 2019， 38（8）： 57-62. [百度学术]

XIN C， LIU H B. A Random Forest Modeling Approach for Predicting Paper Wastewater Effluent Index［J］. China Pulp & Paper， 2019， 38（8）： 57-62. [百度学术]

刘鸿斌，宋留. 相关向量机对废水处理系统出水水质的预测［J］. 中国造纸学报， 2019， 34（2）： 53-59. [百度学术]

LIU H B， SONG L. Prediction of Wastewater Treatment System Effluent Quality by Correlation Vector Machine［J］. Transactions of China Pulp and Paper， 2019， 34（2）： 53-59. [百度学术]

刘鸿斌，李祥宇，杨冲. 基于PCA降维模型的造纸废水处理过程软测量建模［J］. 中国造纸学报， 2018， 33（4）： 50-57. [百度学术]

LIU H B， LI X Y， YANG C. Soft Measurement Modeling of Paper Wastewater Treatment Process Based on PCA Dimensionality Reduction Model［J］. Transactions of China Pulp and Paper， 2018， 33（4）： 50-57. [百度学术]

陶劲松，杨亚帆，李远华. 基于PLS和SVM的纸张抗张强度建模比较［J］. 华南理工大学学报（自然科学版）， 2014， 42（7）： 132-137. [百度学术]

TAO J S， YANG Y F， LI Y H. Comparison of PLS and SVM Based Paper Tensile Strength Modeling［J］. Journal of South China University of Technology （Natural Science Edition）， 2014， 42（7）： 132-137. [百度学术]

李远华，陶劲松，李继庚，等. 基于偏最小二乘法的纸张抗张强度预测模型［J］. 化工学报， 2014， 65（9）： 3544-3551. [百度学术]

LI Y H， TAO J S， LI J G， et al. Paper Tensile Strength Prediction Model Based on Partial Least Squares［J］. CIESC Journal， 2014， 65（9）： 3544-3551. [百度学术]

江伦，满奕，李继庚，等. 基于梯度增强决策树算法的纸张质量软测量模型［J］. 中国造纸， 2020， 39（5）： 37-42. [百度学术]

JIANG L， MAN Y， LI J G， et al. Soft Measurement Model of Paper Quality Based on Gradient-enhanced Decision Tree Algorithm［J］. China Pulp & Paper， 2020， 39（5）： 37-42. [百度学术]

Chen F Z， Wang X Z. Software Sensor Design Using Bayesian Automatic Classification and Back-propagation Neural Networks［J］. Industrial & Engineering Chemistry Research， 1998， 37（10）： 3985-3991. [百度学术]

刘鹏龙，许雄飞，张玮，等. 甲醇制芳烃K-means-PSO-SVR局部建模及优化［J］. 化工进展， 2022， 41（9）： 4691-4700. [百度学术]

LIU P L， XU X F， ZHANG W， et al. Local Modeling and Optimization of K-means-PSO-SVR for Methanol to Aromatics［J］. Chemical Industry and Engineering Progress， 2022， 41（9）： 4691-4700. [百度学术]

Breiman L. Bagging Predictors［J］. Machine Learning， 1996， 24（2）： 123-140. [百度学术]

Freund Y， Schapire R E. A Decision-theoretic Generalization of Online Learning and an Application to Boosting［J］. Journal of Computer and System Sciences， 1997， 55（1）： 119-139. [百度学术]

Burba F， Ferraty F， Vieu P. k-Nearest Neighbour Method in Functional Nonparametric Regression［J］. Journal of Nonparametric Statistics， 2009， 21（4）： 453-469. [百度学术]

Boulesteix A L， Strimmer K. Partial Least Squares： A Versatile Tool for the Analysis of High-dimensional Genomic Data［J］. Briefings in Bioinformatics， 2007， 8（1）： 32-44. [百度学术]

刘佳星. 基于网格搜索超参数优化的支持向量回归［J］. 科学技术创新， 2022（13）： 71-74. [百度学术]

LIU J X. Support Vector Regression Based on Grid Search Hyperparameter Optimization［J］. Scientific and Technological Innovation， 2022（13）： 71-74. [百度学术]

Zhang P， Yin Z Y， Jin Y F， et al. Intelligent Modelling of Clay Compressibility Using Hybrid Meta-heuristic and Machine Learning Algorithms［J］. Geoscience Frontiers， 2021， 12（1）： 441-452. [百度学术]

Luo Z， Hasanipanah M， Bakhshandeh Amnieh H， et al. GA-SVR： A Novel Hybrid Data-driven Model to Simulate Vertical Load Capacity of Driven Piles［J］. Engineering with Computers， 2021， 37（2）： 823-831. CPP [百度学术]

基于机器学习的箱纸板质量预测模型构建及比较

摘要

关键词

1 建模数据整理

1.1 原始数据采集和预处理

1.2 测试和训练数据划分

1.3 特征生成与特征选择