网刊加载中。。。

使用Chrome浏览器效果最佳，继续浏览，你可能不会看到最佳的展示效果，

确定继续浏览么?

复制成功，请在其他浏览器进行阅读

高频摇振系统驱动功率计算

- ORCID：
陈灵方 ¹
- ORCID：
赵建峰 ²
✉
- ORCID：
张鹏 ¹
- ORCID：
刘泽锋 ¹

1. 新疆理工学院，新疆阿克苏，843100； 2. 河南大指造纸装备集成工程有限公司，河南焦作，454950

中图分类号： TS734⁺.8

最近更新：2022-02-22

DOI：10.11980/j.issn.0254-508X.2022.02.011

摘要

高速纸机网部常采用无反作用力的高频摇振器，这种高频摇振器的运动十分复杂。摇振器的驱动功率常根据经验和实践来进行确定，缺少驱动功率理论的计算方法。本课题结合实际，分析了摇振系统数学模型，提出了一种摇振器驱动功率的计算方法，为高频摇振器设计提供理论指导。

关键词

摇振系统; 摇振功率; 高频摇振

长网纸机的成形网除了沿纸机运行方向高速移动外，还要做垂直于纸机运行方向往复高频摆动，这样可以显著提高纸张的匀度和纵横强度，对成纸质量的提高效果明显^[

1]。为实现成形网往复高频摆动，需要对胸辊增设摇振系统，以往采用的曲柄摇杆机构很难达到很高的摇振频率，并且在运行时产生较大的冲击力，因此常用在低速纸机上面；针对高速纸机，现在常使用无反作用力的高频摇振器，这种高频摇振器有2对对称布置的偏重块组成，每对偏重块由1台电机驱动，整个摇振系统共需要2台电机进行驱动^{[参考文献 2

百度学术}2]，以往在进行设计时，驱动电机的功率主要靠经验和实践验证来确定。本课题通过对高频摇振系统的模型进行数学分析计算，提供了一种摇振器驱动功率的计算方法。

1 高频摇振系统模型

1.1　高频摇振器模型

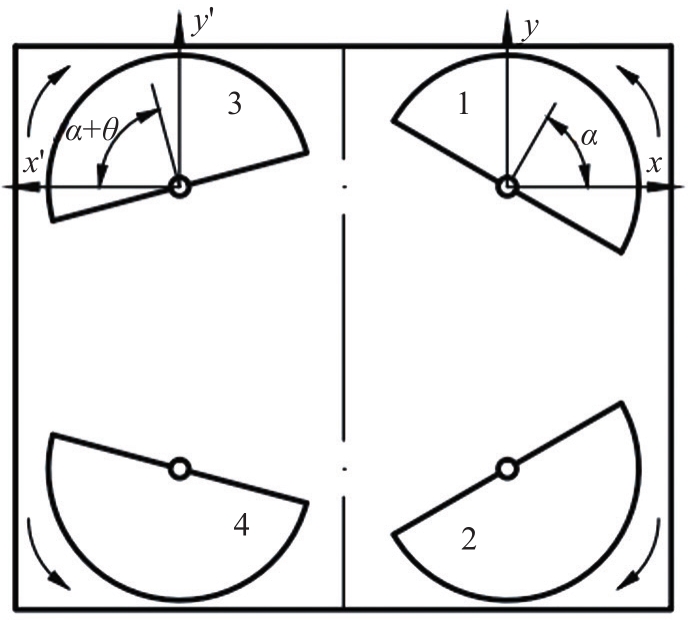
高频摇振器采用2组偏重块（如图1所示），通过改变这2组偏重块的相位角来实现胸辊振幅的变化，并且除了胸辊轴线方向的摇振力外，无其他多余分力，工作十分可靠，无额外冲击力，是一种理想的摇振系统，特别适合于高速纸机^[

3]。

图1 高频摇振器模型

Fig. 1 Model of high-frequency shaking device

以偏重块1的坐标系为基准，2对偏重块在相位角之差为 $θ$ 时摇振力（F）的计算见式（1）。

F = 4 m_{H} r ω^{2} s i n (\frac{θ}{2}) s i n (α + \frac{θ}{2})

（1）

式中， $m_{H}$ 为单块偏重块质量； $r$ 为偏重块质心到圆心的距离； $ω$ 为偏重块转动角速度； $θ$ 为2组偏重块的相位角差； $α = ω t$ ； $t$ 为时间。

1.2　摇振-胸辊模型

摇振-胸辊模型见图2，摇振器和胸辊间使用推杆铰接在一起，胸辊使用横置和竖置共4组板簧支撑。

图2 摇振-胸辊模型

Fig. 2 Model of shaking device-breast roll

注 1—静压滑动导轨；2—偏重块；3—摇振器偏重块支撑箱体；4—球形铰接器；5—板簧；6—胸辊。

2 摇振系统驱动功率计算

2.1　摇振系统模型计算

胸辊作简谐激励下的强迫振动，以机架为基准，胸辊（S）的位移见式（2）。

S = a s i n (ω t + ϕ)

（2）

式中， $a$ 为摇振振幅（一般最大值为12.5 mm，具体数值根据摇振系数确定^[

4]）；

ω

为摇振角速度；

t

为时间；

ϕ

为相位角。

胸辊的速度（V）见式（3）。

V = \frac{d S}{d t} = a ω c o s (ω t + ϕ)

（3）

胸辊的加速度（u）见式（4）。

u = \frac{d V}{d t} = - a ω^{2} s i n (ω t + ϕ)

（4）

胸辊由横置和竖置各2组板簧支撑，计板簧的总刚度为 $C$ ，则板簧对胸辊的作用力（ $F_{1}$ ）计算见式（5）。

F_{1} = C \cdot S = C a s i n (ω t + ϕ)

（5）

胸辊作摇振运动时惯性力（ $F_{2}$ ）见式（6）。

F_{2} = (m + 4 m_{H}) u = - (m + 4 m_{H}) a ω 2 s i n (ω t + ϕ)

（6）

式中， $m$ 为胸辊、链接器、推杆、偏重块支撑箱体以及成形网与浆料等折算的质量之和。

胸辊摇振运动所需要的驱动力（ $F'$ ）见式（7）。

\begin{array}{l} F' = F_{1} + F_{2} \\ = [C a - (m + 4 m_{H}) a ω^{2}] s i n (ω t + ϕ) \end{array}

（7）

由于 $C a$ 可能小于 $(m + 4 m_{H}) a ω^{2}$ 而导致 $C a - (m + 4 m_{H}) a ω^{2} < 0$ ，因此式（7）应变为式（8）。

\begin{array}{l} F' = F_{1} + F_{2} \\ = |C a - (m + 4 m_{H}) a ω^{2}| s i n (ω t + ϕ) \end{array}

（8）

式（1）为摇振器的驱动力，式（8）为胸辊需要的摇振驱动力，在纸机工作中摇振器的驱动力和胸辊需要的摇振驱动力是相等的，相位角也相同，见式（9）和式（10）。

F = F'

（9）

\{\begin{matrix} 4 m_{H} r ω^{2} s i n (\frac{θ}{2}) = |C a - (m + 4 m_{H}) a ω^{2}| \\ ϕ = \frac{θ}{2} \end{matrix}

（10）

式（10）变形后，在一定的转速 $ω$ 和振幅 $a$ 下，摇振器2组偏重块的相位角（ $θ$ ）见式（11）。

θ = 2 a r c s i n \frac{|C a - (m + 4 m_{H}) a ω^{2}|}{4 m_{H} r ω^{2}}

（11）

摇振系统最大摇振力（ $F_{m}$ ）见式（12）。

F_{m} = |C a - (m + 4 m_{H}) a ω^{2}| = 4 m_{H} r ω^{2} s i n \frac{θ}{2}

（12）

2.2　摇振系统功率计算

摇振系统功率（P）计算见式（13）。

P = |F V| = 2 a m_{H} r ω^{3} s i n \frac{θ}{2} |s i n (2 ω t + θ)|

（13）

摇振系统平均功率（ $P_{a}$ ）计算见式（14）。

P_{a} = \frac{\int_{- \frac{θ}{2 ω}}^{\frac{π - θ}{2 ω}} P d t}{\frac{T}{4}} = \frac{4 a m_{H} r ω^{3} s i n \frac{θ}{2}}{π}

（14）

由式（10）和式（14）可得式（15）。

P_{a} = \frac{a ω |C a - (m + 4 m_{H}) a ω^{2}|}{π}

（15）

式（15）建立起了摇振频率、摇振振幅、胸辊质量以及板簧刚度与驱动功率的数学关系。

2.3　摇振性能分析

以一个实际算例进行性能分析，相关参数为：胸辊质量及成形网等质量之和约2000 kg，链接器、推杆和偏重块支撑箱体的质量1800 kg，经计算板簧刚度为 $C =$ 6.015×10⁶ N/m，偏重块质心到圆心的距离为 $r = \frac{4}{3 π} \times 0.19 =$ 0.081 m。

2.3.1　最小满振幅转速

当振幅 $a =$ 12.5 mm时，胸辊达到最大振幅，此时若偏重块相位角 $θ = π$ ，则对应的偏重块最小转速为最小满振幅转速。根据式（10）可以求得最小满振幅转速为 $n \approx$ 235 r/min。

计算得到的最小满振幅转速的意义在于说明在此种工况下，胸辊要达到最大振幅，偏重块转速必须达到235 r/min以上；如果偏重块转速小于235 r/min，不论如何调节摇振器偏重块相位角，胸辊都达不到最大振幅。

2.3.2　胸辊允许最大质量

当振幅 $a =$ 12.5 mm时，胸辊达到最大振幅，此时若偏重块相位角 $θ = π$ ，偏重块转速达到500 r/min时，则此时对应的胸辊质量为胸辊允许最大质量，很显然此时摇振系统处于极限状态。

根据式（10），应只考虑 $C a - m a ω^{2} < 0$ 的情况，经计算 $m$ 最大值m_max=7500 kg，则胸辊的允许最大质量不大于4900 kg。

胸辊允许最大质量的意义在于说明摇振器在极限的工况下的最大工作能力。

2.3.3　摇振系统驱动功率曲线

当振幅 $a =$ 12.5 mm时，胸辊达到最大振幅，根据式（15）计算可以得到，驱动功率与摇振频率曲线如图3所示。

图3 驱动功率与摇振频率曲线

Fig. 3 Curve of between driving power and shaking frequency

当 $C a - m a ω^{2} = 0$ 时，对应的转速为344 r/min，此时理论上摇振系统所需功率为零，摇振系统摇振频率等于系统固有频率，在针对特定纸机进行设计时需要注意这个特性，一方面远离共振点以防止共振带来破坏等不利影响，另一方面通过上图可知，合理选择工作时的摇振频率，可以控制驱动功率。

3 算例分析

以前述胸辊-摇振系统进行算例分析，车速800 m/min，为了减小驱动功率，摇振频率选择380～430 r/min之间，根据式（16）^[

5]可知：

I = \frac{n^{2} \cdot a}{v}

（16）

式中， $I$ 为摇振系数，一般取值为3000～4000； $n$ 为摇振频率； $a$ 为行程（振幅的2倍）； $v$ 为车速。则在此工况下，振幅取值为±7.5～12.5 mm。

取摇振系数 $I = 3500$ ，摇振频率 $a =$ 400 r/min，行程17.5 mm( $a =$ ±8.75 mm)，车速 $v =$ 800 m/min，在此工况下，经计算摇振系统所需平均功率为2.14 kW，瞬时最大功率为3.36 kW。

纸机最大车速 $v =$ 1000 m/min，取摇振系数 $I = 4500$ ，摇振频率 $n =$ 500 r/min；行程 $18 m m (a = \pm 9 m m)$ ，此工况为纸机最大工况，经计算摇振系统所需平均功率为9 kW，瞬时最大功率为14.13 kW。

4 结　语

本课题推导了一种摇振系统驱动功率的计算方法，确定了胸辊质量、摇振频率、摇振振幅及板簧刚度之间的数学关系，同时对摇振器也提出了最小满振幅转速和胸辊允许最大质量两项性能指标。该计算方法在实际设计工作中已多次应用，并进行了案例计算，理论计算结果满足使用要求。但本课题所述高频摇振系统驱动功率计算仍存在需要研究的方面和不足，如摇振系统驱动方式和结构对驱动电机的功率选择有很大影响、摇振系统工作过程中2台伺服驱动电机输出功率不一致、胸辊采用滑动轴承支撑工况下的功率计算问题等，将在后期的工作中进行相关研究。

参考文献

戴杰明，崔良溶，张海晖.自平衡高频摇振机的原理与应用［J］.中华纸业， 2013，34（16）：48-50. [百度学术]

DAI J M， CUI L R， ZHANG H H.The principles and applications of self-balanced high frequency SHAKE［J］.China Pulp & Paper Industry， 2013， 34（16）：48-50. [百度学术]

叶钢锋，张海晖.自平衡高频摇振器的驱动与自动化控制［J］.中国造纸， 2014， 33（2）：52-55. [百度学术]

YE G F， ZHANG H H.Automatic Control and Driving of High Frequency Counterforce Free Shaker［J］.China Pulp & Paper， 2014， 33（2）：52-55. [百度学术]

陈灵方，赵建峰，盛海鹏，等.高频摇振系统数学模型研究［J］.中华纸业， 2020，41（2）：44-46. [百度学术]

CHEN L F， ZHAO J F， SHENG H P， et al.A Research on Mathematical Model for High Frequency Shaking Systems［J］.China Pulp & Paper Industry， 2020， 41（2）：44-46. [百度学术]

王忠厚，许志晔.制浆造纸工艺计算手册［M］.北京：中国轻工业出版社， 2011：251-252. [百度学术]

WANG Z H， XU Z Y. Handbook of Calculations in Pulping and Papermaking［M］. Beijing：China Light Industry Press， 2011：251-252. [百度学术]

张　锋，高致富，刘　欢. 一种高速纸机新型摇振装置的设计［J］.中国造纸， 2013， 32（12）： 45-48. [百度学术]

ZHANG F， GAO Z F， LIU H. Design of a New Shaking Device for High Speed Paper Machine［J］.China Pulp & Paper， 2013， 32（12）： 45-48. [百度学术]

CPP [百度学术]

高频摇振系统驱动功率计算

摘要

关键词

1 高频摇振系统模型

1.1 高频摇振器模型

1.2 摇振-胸辊模型

2 摇振系统驱动功率计算

2.1 摇振系统模型计算

2.2 摇振系统功率计算

2.3 摇振性能分析