网刊加载中。。。

使用Chrome浏览器效果最佳，继续浏览，你可能不会看到最佳的展示效果，

确定继续浏览么?

复制成功，请在其他浏览器进行阅读

纸张涂层研磨碳酸钙颜料渗吸特性的分形模型建立及修正

- ORCID：
刘国栋 ^1,2
✉
- ORCID：
王晨曦 ^1,2
- ORCID：
付思佳 ^1,2
- ORCID：
高修安 ^1,2
- ORCID：
李靖 ^1,2

1. 陕西科技大学轻工科学与工程学院，陕西西安，710021； 2. 轻化工程国家级实验教学示范中心，中国轻工业功能印刷与运输包装重点实验室，陕西省造纸技术及特种纸品开发重点实验室，中国轻工业纸基功能材料重点实验室，陕西西安，710021

中图分类号： TS727⁺.3

最近更新：2021-12-22

DOI：10.11980/j.issn.0254-508X.2021.12.006

目录contents

摘要

本研究测量和表征了研磨碳酸钙（GCC）颜料渗吸性能，分析了GCC颜料渗吸特性与经典渗吸模型（Lucas-Washburn模型、Bosanquet模型和纯惯性力模型）的内在关系。通过分形理论求解计算了GCC颜料的分形特征，从渗吸动力学和分形结构两方面建立了GCC颜料渗吸的分形模型，引入渗吸量修正因子和形状因子对分形模型进行进一步修正，修正后的渗吸分形模型完全匹配了GCC颜料全过程的渗吸特性。构建的渗吸模型为GCC颜料渗吸特性的预测和具有良好渗吸特性的颜料开发提供一定的技术支持。

关键词

研磨碳酸钙; 渗吸特性; 分形维数; 渗吸模型

印刷流体在纸张涂层中的传输直接由涂层本身的吸收性能所决定。很多印刷质量问题，如墨斑、色彩的均匀性、洇色等都与纸基表面涂层材料的吸收特性有重要关系。印刷过程中，印刷流体（诸如油墨）在纸基表面的吸收基本上分为两个阶段，一种是外在印刷压力条件下的有压吸收，通常称为加压渗透^[

1]；另一种是在没有外在压力情况下的吸收，或者是当印刷压力撤离后，印刷流体在纸面上的进一步吸收，通常称为毛细系统的自由渗吸，简称渗吸^{[参考文献 2

百度学术}2]。对于具有外在压力的加压渗透，印刷压力作为外力因素，在印刷过程中可以进行适当的调整及补偿，来修正压力不当对渗透产生的影响，进而确保图文信息在纸面的良好成像。而对于自由渗吸，其渗吸过程主要依靠纸基材料形成的多孔网络，且印刷过程中自由渗吸的持续时间比加压渗透的时间长很多^{[参考文献 3

百度学术}3]，更容易对印刷成像造成重要影响。因此相比加压渗透，毛细系统支配下的自由渗吸对印刷流体在纸面的准确成膜（或者成像）具有更重要的作用。

纸基材表面的涂层材料用来改善基材的印刷性能^[

4]，本质上是通过结构的改变来加强基材对外部作用流体的渗吸性能。一般涂层材料由颜料、胶黏剂及添加剂组成，其中颜料本身的渗吸特性对于整个涂层的吸收起着决定作用。因此颜料渗吸特性的研究对改善纸基材料的印刷适性有着确切的科学意义。涂层颜料本身就是一种多孔介质，对于多孔介质材料的渗吸模型通常是基于渗吸动力学系统来建立的，诸如经典的Lucas-Washburn（简称L-W）模型^{[参考文献 5

百度学术}5]，在根时间标度下，阐明了渗吸特性与渗吸根时间（

\sqrt[]{t}

）的线性关系，同时也说明了渗吸量与多孔介质等效毛细管半径成正比的关系。虽然该模型作为多孔介质最经典的模型之一，但后续的研究发现，模型的预测值与实际的渗吸特性仍有较大的差异。Brú等人^{[参考文献 6

百度学术}6]通过实验确定了与纸张涂层类似材料的渗吸量与时间标度之间的函数关系是时间指数的0.40～0.49左右，并以此为依据指出了经典L-W方程不能很好的描述实验现象，是由于时间标度的0.5函数关系造成的。Schoelkopf等人^{[参考文献 7

百度学术}7]研究以研磨碳酸钙（GCC）为主体的涂层材料渗吸时，也发现了L-W模型描述渗吸的实验偏差。Ridgway等人^{[参考文献 8

百度学术}8]在研究改性研磨碳酸钙（GCC）的渗吸特性时，发现不能用L-W模型解释实验渗吸的原因是忽略了渗吸过程多孔介质中惯性力的累积效应。由于渗吸初期渗吸流体质量很小，对应的自身重力和黏性阻力也很小，故可忽略不计，起主要支配作用的是毛细力和惯性力。因此Quéré^{[参考文献 9

百度学术}9]建立的纯惯性力模型用来描述渗吸的初期特性，即渗吸量在渗吸时间的标度下，与等效毛细管半径成反比。与L-W模型和纯惯性力渗吸模型相比，考虑惯性力、毛细力、黏性力支配的Bosanquet渗吸模型可以更综合的描述渗吸动力学系统。文献[10]对比三者模型的区别，通过大量的仿真发现Bosanquet渗吸模型中包括了纯惯性力模型和L-W模型，在渗吸初期Bosanquet渗吸模型与纯惯性力模型是一致的。随着渗吸的进行，在渗吸的后期，Bosanquet渗吸模型逐渐转变为L-W渗吸模型。因此具有更加综合渗吸动力学系统的Bosanquet模型可以是描述多孔介质渗吸特性的优选方案之一。

在建立多孔介质渗吸模型的过程中，除了渗吸动力学系统方面的考虑外，还应该考虑多孔介质的结构因素，但自然界中多孔介质（如GCC）的结构是一种复杂无序的网络，根本无法用传统的欧式几何去描述和表征。已有大量的研究表明^[

11-12]，自然界中大部分多孔材料的随机无序结构，在一定尺寸范围上满足分形特征，可以用非欧式几何的分形理论来加以精确描述。Liu等人^{[参考文献 13-14}13-14]证明了纸张涂层材料GCC在一定尺度上具有分形结构，并建立考虑惯性力累积效应和表面粗糙度因子的渗吸分形结构模型，成功匹配了实验初期的渗吸，但并没有匹配全阶段渗吸的过程，且模型建立及计算十分复杂，很难在实际过程中进行便捷的应用。

因此，在上述基础上，本研究针对纸张涂层材料渗吸特性，考虑渗吸动力学和多孔介质分形特征两方面因素，构建GCC颜料的渗吸模型，为纸张涂层材料整体渗吸特性的模拟和预测提供模型和方法支持，为涂层材料渗吸的开发及结构改进提供科学的理论依据。

1 GCC颜料渗吸特性及孔结构的测量

1.1　实验材料

GCC颜料选择瑞士Omya公司生产的3种典型的纸张颜料产品，分别是Hydrocarbon 60ME（标记为：cbGCC），60％（质量占比，下同）粒径小于2 μm；Hydrocarbon 90ME（标记为：fbGCC），90％粒径小于2 μm；Covercarb 75ME（标记为：fnGCC），75％粒径小于1 μm。正十六烷（陶氏化学公司，美国）作为一种非反应性润湿液体，经常用于涂层颜料的渗吸测量^[

3]。其物理参数如表1所示。

表1 渗吸流体正十六烷的物理性能参数

Table 1 Physical properties of imbibition fluid hexadecane

黏度（ $σ$ ） $/$ Pa·s	密度（ $ρ$ ）/kg·m^-3	表面张力（ $μ$ ） /N·m^-1	接触角（ $θ$ ，对颜料）/（°）
0.003	773	0.030	0

黏度（

σ

）

/

Pa·s

密度（

ρ

）/kg·m^-3

表面张力（ $μ$ ）

/N·m^-1

接触角（

θ

，对颜料）/（°）

0.003

773

0.030

1.2　渗吸样本的制作及测量

为了更好测量纸张涂层颜料的渗吸特性，需要进行样本制作。使用特制的钢制模^[

15]在恒定压力p =（259.4 ± 2.7）MPa下通过过滤进行脱水，并在恒温烘箱中进行干燥，将涂料制成片状形式。样本完成后，裁切成横截面大约为12 × 12 mm²大小的块状，并通过圆盘研磨机，将样品的6个横截面进行修饰并打磨至光滑。为了减少测量过程中外表面对润湿造成的影响，在渗吸样本的垂直底部侧面涂布一圈硅树脂，外表面的其余部分保持未涂布状态如图1(a)所示。

图1 测量示意图

Fig. 1 Survey diagram

测量过程中，测量装置安放在恒温恒湿实验室，温度为(23.0 ± 5)℃，相对湿度达到50%。将每个样品置于隔离罩中并用干燥氮气冲洗，样品平衡48 h。测量时，将样品缓慢地向渗吸液体靠近，在液体接触样品的瞬间，与计算机连接的天平（梅特勒-托利多XSE105）自动记录润湿液体渗吸到颜料中的质量（见图1），测量精度大约为0.1 mg，每秒进行10次变化的测量，并在进行5次测量后通过与天平相连的计算机得出平均渗吸速率。

1.3　GCC颜料孔结构的测量

通过压汞仪（AUTOPORE Ⅳ，麦克公司，美国）实现对碳酸钙颜料的孔结构测量，为了去除样品中的水分及水蒸气，样品需在烘箱（105℃）中至少干燥24 h。每种样品的取样量大约0.7 g（0.3 cm³），压汞仪最大应用压力为414 MPa，仪器可测的最小孔径为4 nm。考虑到压汞过程中材料的压缩、汞的压缩及样品夹具的变形，需要对孔体积分布、孔径分布等特征曲线进行修正^[

16]，在孔体积分布、孔径分布的基础上，根据式(1)^{[参考文献 17

百度学术}17]进行累积孔面积的计算，最终完成对碳酸钙涂层颜料结构的测量。

A = \frac{0.02253}{m} \int_{0}^{V} P d V

（1）

式中， $A$ 为累积孔面积； $m$ 为碳酸钙颜料的质量； $V$ 为总孔隙体积； $P$ 为测得的压汞仪压力。

2 GCC颜料的分形结构表征

GCC颜料涂层的渗吸特性，主要由颜料颗粒之间形成的孔结构决定，孔结构形成的多孔网络及通道是提供液体渗吸和流动的基础。由于颜料颗粒之间的堆砌网络和通道是一种复杂、无序的结构，很难用经典的欧式几何去描述和表征，但是非欧式分形几何的出现，给无序随机的多孔结构带来了有效的表征手段。同时，文献[

13-14]证明GCC颜料在特定的尺度下具备分形特征。因此，可以用孔结构的分形维数来表征GCC颜料与多孔介质材料的无规则孔结构特征。

采用压汞法对颜料孔隙结构的分形维数进行测量，孔隙体积、半径及分形维数之间的关系如式(2)所示。

\frac{d V (r)}{d r} \propto (D_{f} - 2) (3 - D_{f}) r^{2 - D_{f}}

（2）

将式(2)移项得到式(3)。

d V (r) \propto (D_{f} - 2) (3 - D_{f}) r^{2 - D_{f}} d r

（3）

由于

r^{2 - D_{f}} d r = \frac{d r^{3 - D_{f}}}{3 - D_{f}}

（4）

因此，式(3)可以改写为式(5)。

d V (r) \propto (D_{f} - 2) d r^{3 - D_{f}}

（5）

对式(5)两边积分得式(6)。

V (r) \propto (D_{f} - 2) r^{3 - D_{f}}

（6）

对式(6)两边取对数得式(7)。

l g V (r) \propto (3 - D_{f}) l g r + l g (D_{f} - 2)

（7）

式中， $r$ 为孔隙半径； $V (r)$ 为压汞实验测得的孔隙半径 $r$ 对应的孔隙体积。

以上分析表明， $V (r)$ 和 $r$ 在双对数坐标上呈直线关系，可用回归拟合法来计算分形维数 $D_{f}$ 。

3 基于分形结构的GCC颜料渗吸模型的构建

传统意义上多孔材料的渗吸模型常将多孔介质等同为具有等效半径的毛细管结构，主要考虑流体渗吸过程中的动力学系统，如渗吸过程中的黏性阻力、流体的惯性力、毛细驱动压力和流体自身的重力等，来建立渗吸模型，并没有考虑孔结构等方面的因素，尤其对于杂乱无规则的孔结构特征，会对渗吸过程造成重要影响，这也是理论渗吸模型与实际渗吸存在差距的主要原因之一^[

18-19]。因此，考虑渗吸过程动力学和结构两方面因素将会进一步缩小渗吸模型与实际渗吸的差距。

假设在多孔介质中的特定尺寸范围内具有分形特征，则满足分形关系的孔结构参数计算见以下公式^[

20-21]。

单位孔隙中总孔隙的横截面积 $A_{p}$ 计算见式(8)。

A_{p} = \frac{π λ_{m a x}^{2}}{4 \frac{D_{f}}{(2 - D_{f})} (1 - φ)}

（8）

式中， $φ$ 为多孔介质的孔隙率； $D_{f}$ 为孔隙分形维数； $λ_{m a x}$ 为分形尺度范围的最大孔径。

单位孔隙的总横截面积 $A_{u}$ 计算见式(9)。

A_{u} = \frac{A_{p}}{φ} = \frac{π λ_{m a x}^{2}}{4 \frac{D_{f}}{(2 - D_{f})} \frac{(1 - φ)}{φ}}

（9）

单位孔隙的总横截面积 $A_{u}$ 的孔数量 $N$ 计算见式(10)。

N (\geq λ) = {(\frac{λ_{m a x}}{λ})}^{D_{f}}

（10）

式中， $λ$ 为分形尺度范围的孔径尺寸。

多孔介质任意横截面上 $A_{f}$ 中的总孔隙数目 $N_{f}$ 计算见式(11)。

N_{f} (\geq λ) = \frac{A_{f}}{A_{u}} N = \frac{4 A_{f}}{π λ_{m a x}^{2 - D_{f}} {\frac{(2 - D_{f}) φ}{D_{f} (1 - φ)}}^{- D_{f}}}

（11）

对式(11)进行微分，可以得出孔径尺度变化 $λ$ 和 $λ + d λ$ 范围内的孔隙数目见式(12)。

- d N_{f} = \frac{4 A_{f}}{π λ_{m a x}^{2 - D_{f}} {\frac{(2 - D_{f}) φ}{(1 - φ)}}^{- (D_{f} + 1)}} d λ

（12）

假设流体以均匀的活塞方式向上渗吸到毛细管中（沿z轴方向），根据哈根-泊萧叶方程，单个毛细管渗吸的速率计算见式(13)。

q (λ) = \frac{π}{128} \frac{λ^{4}}{μ L} \frac{4 σ c o s θ}{λ}

（13）

式中， $ρ$ 为液体的密度； $σ$ 为液体表面张力； $μ$ 为液体的黏度； $θ$ 为接触角； $L$ 为涂料流动路径的实际长度。

通过对式(13)积分，可以获得通过多孔介质横截面积的总流速见式(14)。

\begin{array}{l} Q = - \int_{λ_{m i n}}^{λ_{m a x}} q (λ) d N_{f} = \frac{σ c o s θ (2 - D_{f}) A_{f} φ}{8 μ L (3 - D_{f}) (1 - φ)} \\ [λ_{m a x} (1 - ξ^{3 - D_{f}})] \end{array}

（14）

其中 $ξ = λ_{m i n} / λ_{m a x}$ 。一般在多孔介质中 $ξ < 10^{- 2}$ ，二维空间中的分形维数满足 $1 < D_{f} < 2$ ， $3 - D_{f} > 1$ ，所以 $ξ^{3 - D_{f}} < < 1$ ^[

22]。

因此式(14)可以简化为式(15)。

Q = \frac{σ \cdot c o s θ (2 - D_{f}) A_{f} φ}{8 μ L (3 - D_{f}) (1 - φ)} λ_{m a x}

（15）

通过孔隙面积（ $A_{f} φ$ ）的平均渗吸速度计算见式(16)。

v = \frac{Q}{A_{f} φ} = \frac{σ \cdot c o s θ (2 - D_{f}) λ_{m a x}}{8 μ L (3 - D_{f}) (1 - φ)}

（16）

由于渗吸作用增加的质量M如式(17)。

M = ρ A_{f} φ L

（17）

对式(17)关于时间 $t$ 求导得到式(18)。

\frac{d M}{d t} = ρ A_{f} φ v

（18）

将式(16)带入式(18)，可以得到式(19)。

\frac{d M}{d t} = \frac{a}{M}

（19）

其中常数a计算见式(20)。

a = \frac{σ \cdot c o s θ (2 - D_{f}) {(A_{f} φ ρ)}^{2} λ_{m a x}}{8 μ (3 - D_{f}) (1 - φ)}

（20）

对式(19)求积分得到式(21)。

M = \sqrt[]{t \cdot \frac{σ \cdot c o s θ (2 - D_{f}) {(A_{f} φ ρ)}^{2} λ_{m a x}}{4 μ (3 - D_{f}) (1 - φ)}}

（21）

式(21)为在考虑多孔介质分形结构的渗吸质量和渗吸时间的函数关系，可以用来反映多孔介质的渗吸特征，从以上公式中可以看出，渗吸量不仅与流体渗吸的流动性质有关，还与多孔介质结构的特征（ $D_{f}$ ）有重要关系。

4 GCC颜料渗吸特性分析及模型验证

4.1　GCC颜料的孔结构特征

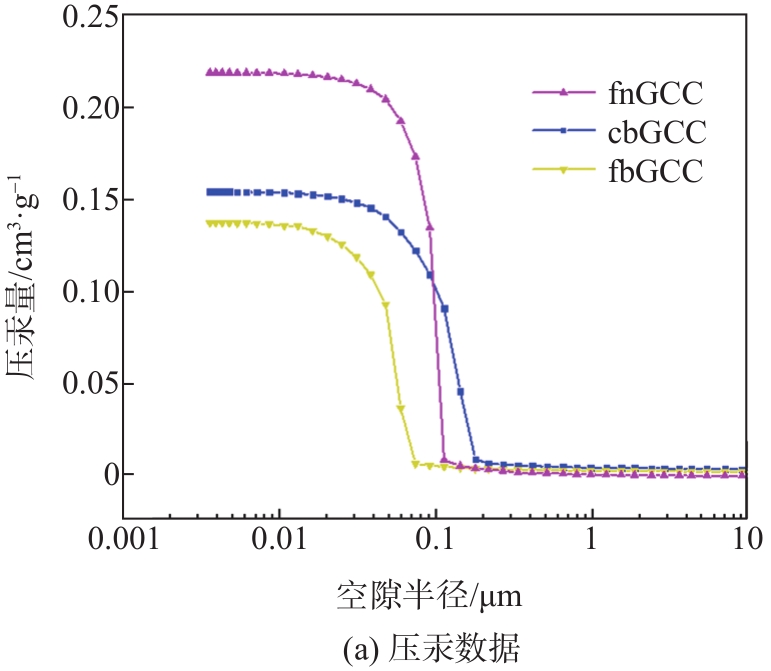
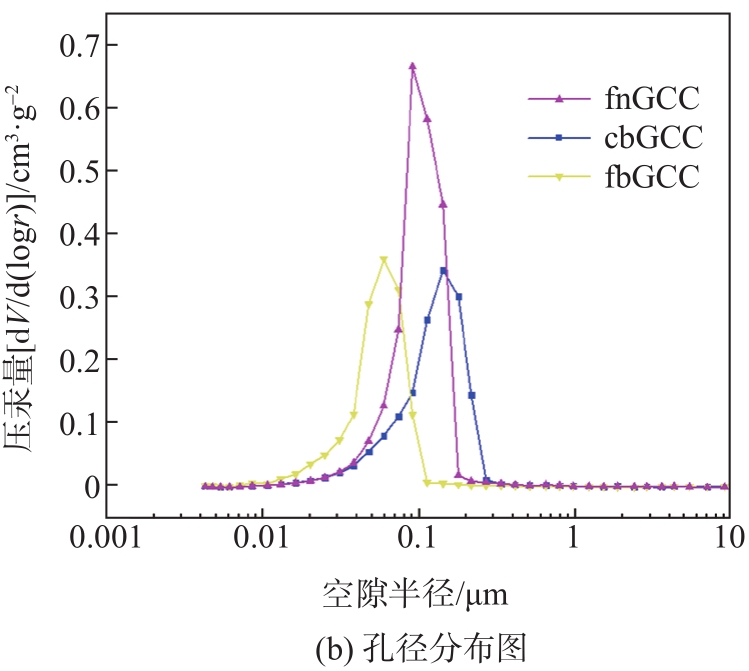
根据压汞法对GCC颜料样本的孔结构特征进行测量及校正，结果如图2所示。从图2中可以看出，fnGCC、cbGCC和fbGCC压汞孔体积依次减少，孔径分布的曲线峰值说明，fbGCC中小孔所占的比例较大，而cbGCC中大孔所占的比例大，但同时也包含了一些小孔，fnGCC具有更均匀的孔径分布。结合孔径分布和孔体积的变化，若假设多孔介质都可以等效为毛细管，则等效毛细管等效半径从小到大排列的顺序依次是 $R_{f b G C C}$ < $R_{c b G C C}$ < $R_{f n G C C}$ 。颜料样本根据结构测量，计算的孔隙结构特征参数见表2。

图2 GCC系列样本的压汞数据和孔径分布图

Fig. 2 Intrusion volume and pore size distribution with mercury porosimetry of GCC samples

表2 GCC系列样本孔隙结构的结构特征参数

Table 2 Structure characteristics of pore structure of GCC samples

样品	总孔体积/cm³·g^-1	固相密度/g·cm^-3	孔隙率/%	累积孔面积/g·cm^-2
cbGCC	0.151	2.705	29.39	21.725
fbGCC	0.135	2.714	27.05	17.926
fnGCC	0.220	2.775	37.68	23.412

4.2　GCC颜料渗吸特性与经典模型的匹配问题

按照上述的渗吸测量方法和装置对3类GCC颜料渗吸特性进行测量，在渗吸时间（t）标度下，渗吸特性结果如图3和图4所示。

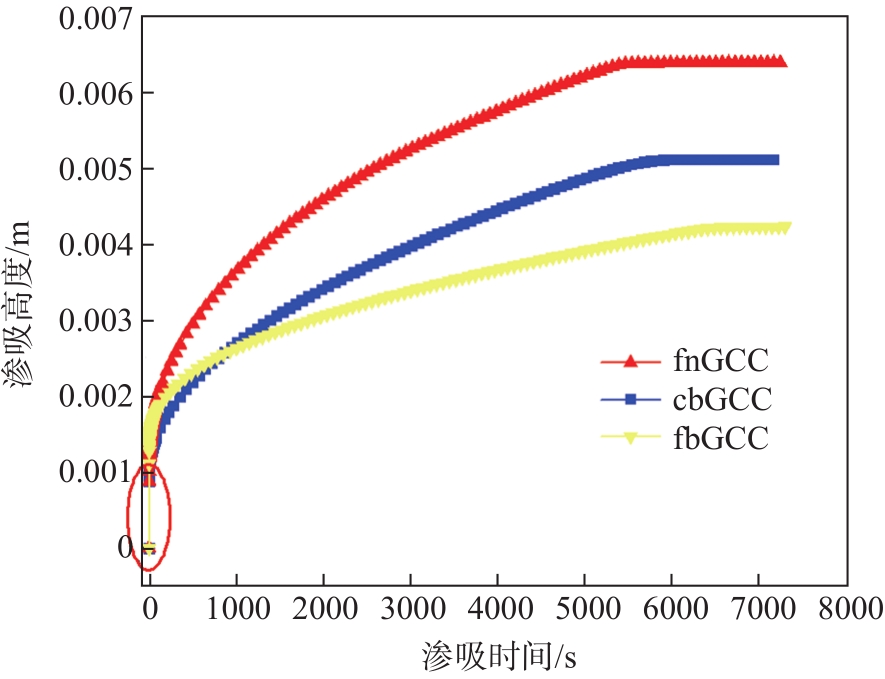
图3 时间机制下GCC的整个渗吸过程

Fig. 3 Complete imbibition with time regime for GCC

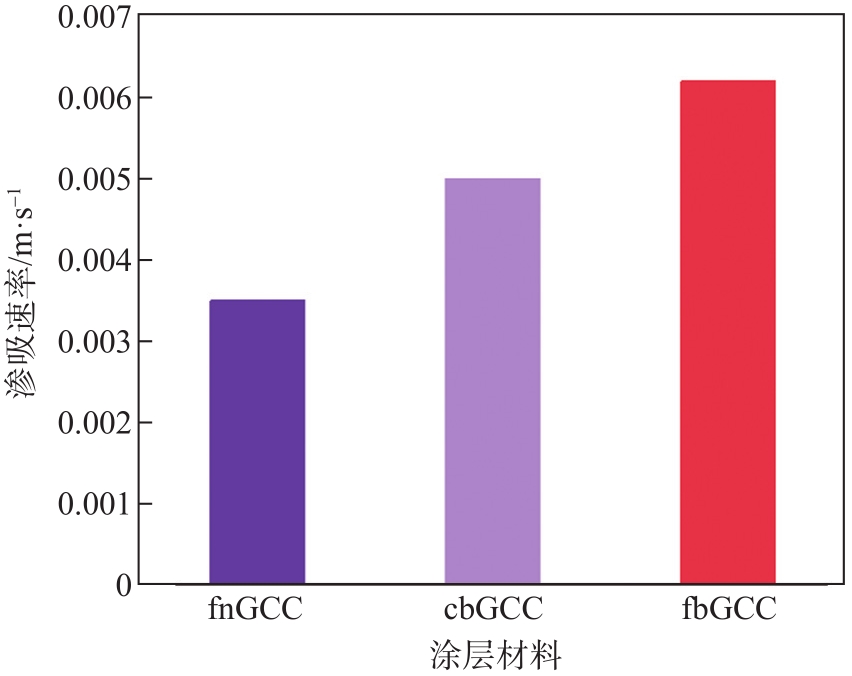
图4 时间机制下GCC的初始渗吸速率

Fig. 4 Initial imbibition with time regime for GCC

结果表明，在渗吸的时间机制下，渗吸量在初期与时间成线性变化的关系（图3中标记区域，具体的渗吸速率如图4所示），之后渗吸量与渗吸时间呈幂衰减函数关系，这与Bosanquet模型所描述的渗吸具有一定的相关性，由于Bosanquet渗吸机制在初期与纯惯性力渗吸模型一致，渗吸速率与等效毛细管半径成反比，结合孔隙结构的等效毛细管半径关系（ $R_{f b G C C}$ < $R_{c b G C C}$ < $R_{f n G C C}$ ）可知渗吸速率为： $v_{f n G C C}$ < $v_{c b G C C}$ < $v_{f b G C C}$ ，与图4表示结果一致。

在渗吸的根时间（ $\sqrt[]{t}$ ）标度下，GCC渗吸特性表现为线性关系，如图5所示。与经典的L-W渗吸机制表达形式一致，但是出现2个不同的渗吸速率，同时初始的渗吸速率大于后期的渗吸速率。文献[

23]将在根时间机制下出现的不同渗吸率，称为渗吸的分区现象，并认为初期较大的渗吸率是由于多孔介质的渗吸惯性力累积效应引起的。因此初期的渗吸分析应该归结为惯性力的渗吸行为，渗吸速率随着等效半径的增大而减小，与测量根时间机制下的渗吸速率变化一致，如图6(a)所示。随着渗吸的持续进行，渗吸过程的毛细力作用逐渐明显，惯性力的作用逐渐减弱，渗吸表现为毛细力支配下的L-W机制，因此渗吸速率与多孔介质的等效毛细管半径成正比，样品在此阶段的渗吸速率为：

v_{f n G C C}

v_{c b G C C}

v_{f b G C C}

，这与测量的渗吸特性一致，如图6(b)所示。

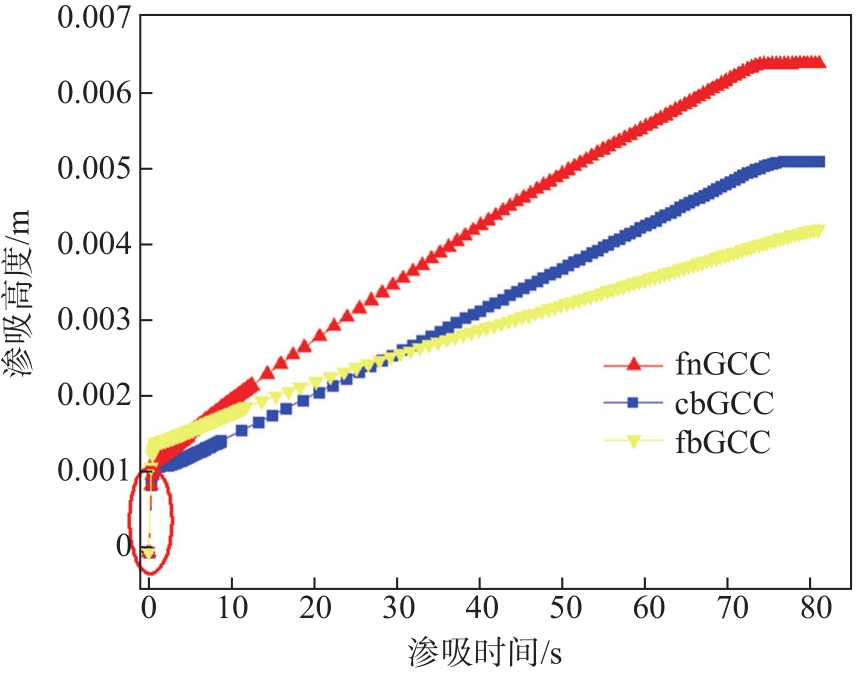
图5 根时间机制下GCC的整个渗吸过程

Fig. 5 Complete imbibition with square root time regime for GCC

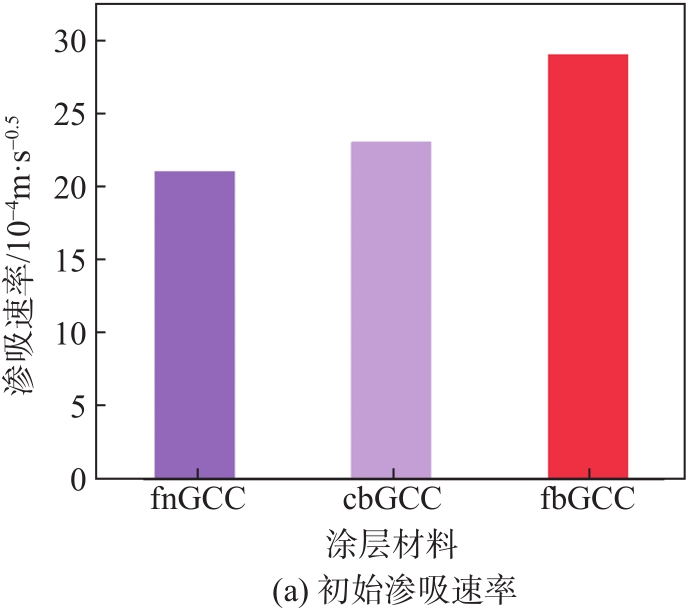
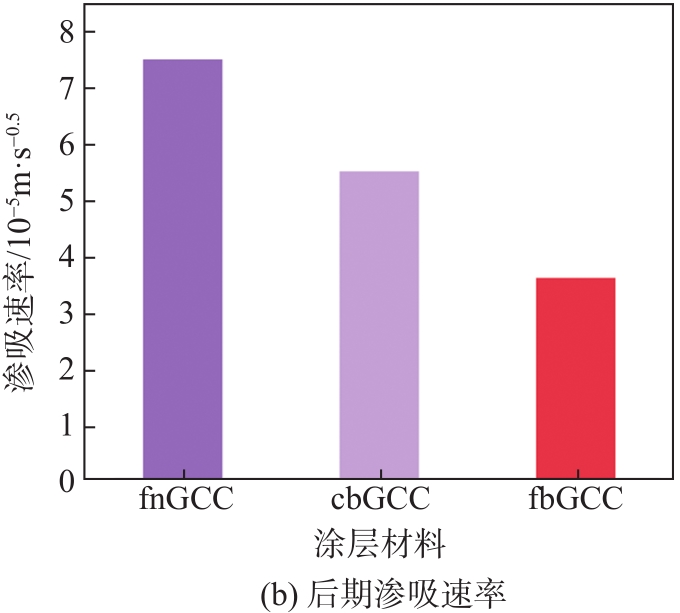
图6 根时间机制下GCC的渗吸速率

Fig. 6 Imbibition rate with root time regime for GCC

综合上述测量GCC颜料的时间和根时间标度下的渗吸行为，整体表现为初期的惯性力渗吸行为和后期的L-W渗吸行为。由于Bosanquet渗吸机制在初期与惯性力渗吸行为是一致的，后期渗吸与经典的L-W渗吸行为相同，包括了上述GCC颜料实验渗吸的特征。因此，理论上讲，可以通过Bosanquet渗吸机制对GCC颜料整体的渗吸特性进行匹配和描述。将渗吸流体的物理参数和GCC颜料的基本孔结构参数代入Bosanquet渗吸机制模型中，得到的实验渗吸与理论渗吸匹配结果，如图7所示。

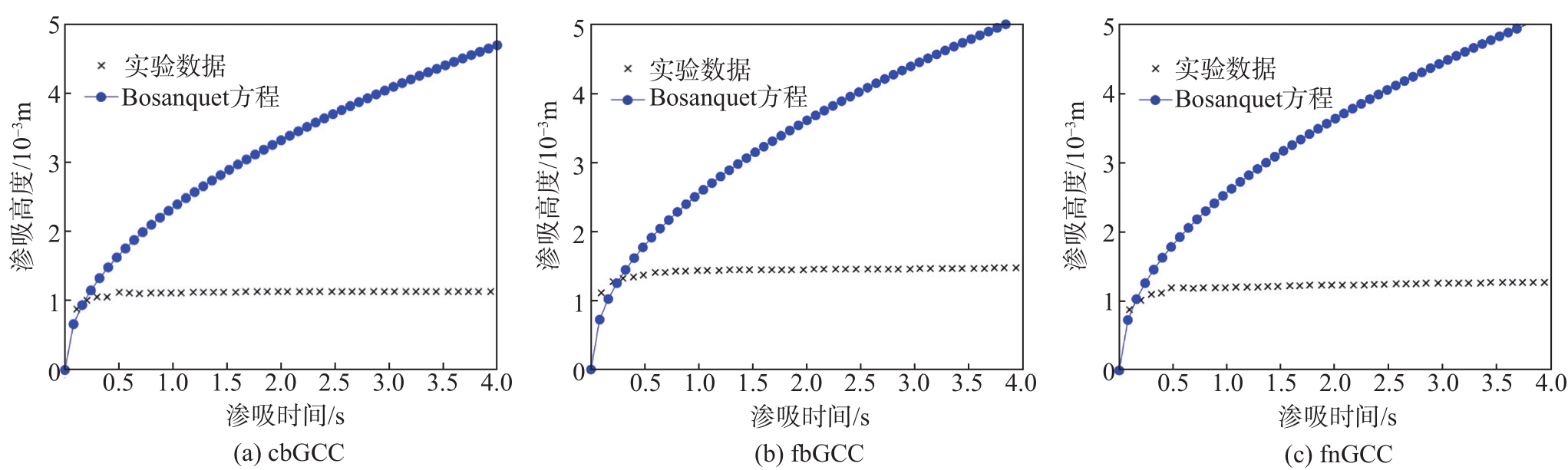
图7 GCC的渗吸对比图

Fig. 7 Permeation comparison chart of GCC

从实验渗吸与理论渗吸匹配结果可以看出，当试图用Bosanquet渗吸模型去描述GCC颜料整体的渗吸行为时，理论测量值仅在渗吸初期（t < 0.25）与实验渗吸有较好的吻合度，但是整体渗吸与实际测量仍有很大的差距。

虽然Bosanquet渗吸模型不能够定量地说明样品的渗吸结果，但可以定性描述GCC颜料渗吸初期和后期渗吸行为。主要原因可能是Bosanquet方程在模型构建时，在假设理想规则的孔隙形貌条件下，只考虑了渗吸过程的动力学传输机制，并没有考虑多孔介质中随机分布、杂乱无序的孔隙结构特性。

4.3　分形维数与GCC颜料孔隙结构及渗吸特性间的关系

在渗吸建模过程中，要考虑多孔介质中杂乱无序的孔隙结构特性，需计算出多孔介质的分形特征，即分形维数，并查明分形维数与孔隙结构及渗吸特性之间的关系。GCC颜料（fbGCC、cbGCC和fnGCC）在特定尺度下孔隙结构的分形分析按式(7)计算，结果如图8所示，最终的分形维数计算结果如表3所示。

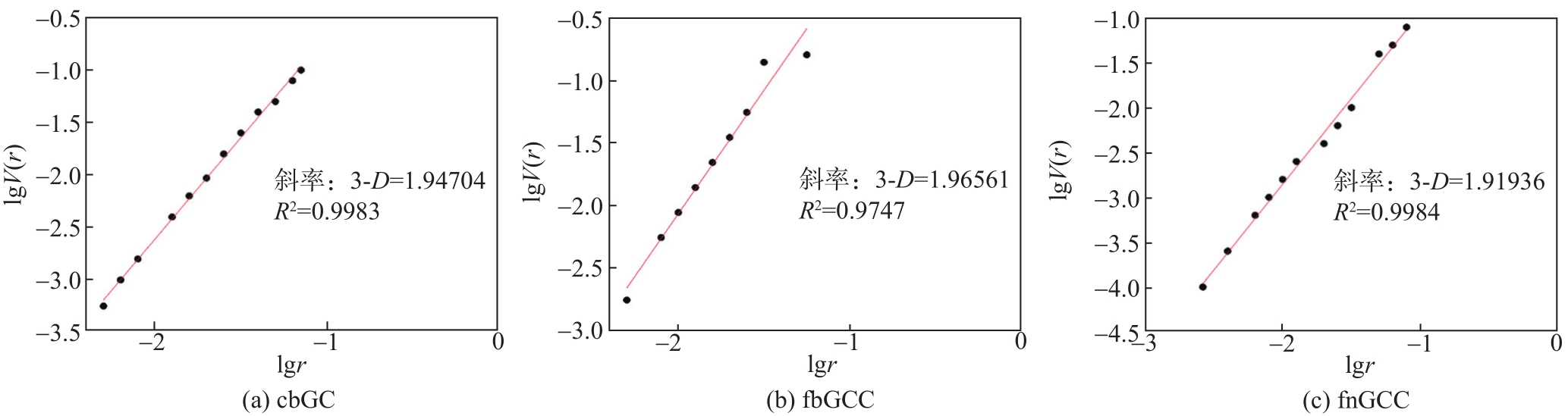
图8 GCC颜料分形结构分析

Fig. 8 Fractal structure analysis of GCC

表3 GCC颜料的孔隙结构分形维数

Table 3 Fractal dimension of GCC pigments

样品	斜率3-D	分形维数D	相关系数R²
cbGCC	1.94704	1.05296	0.9983
fbGCC	1.96561	1.03439	0.9747
fnGCC	1.91936	1.08064	0.9984

GCC颜料分形维数与总孔隙体积、总孔表面积、渗吸特性以及孔隙率的分析，结果如图9及图10所示。

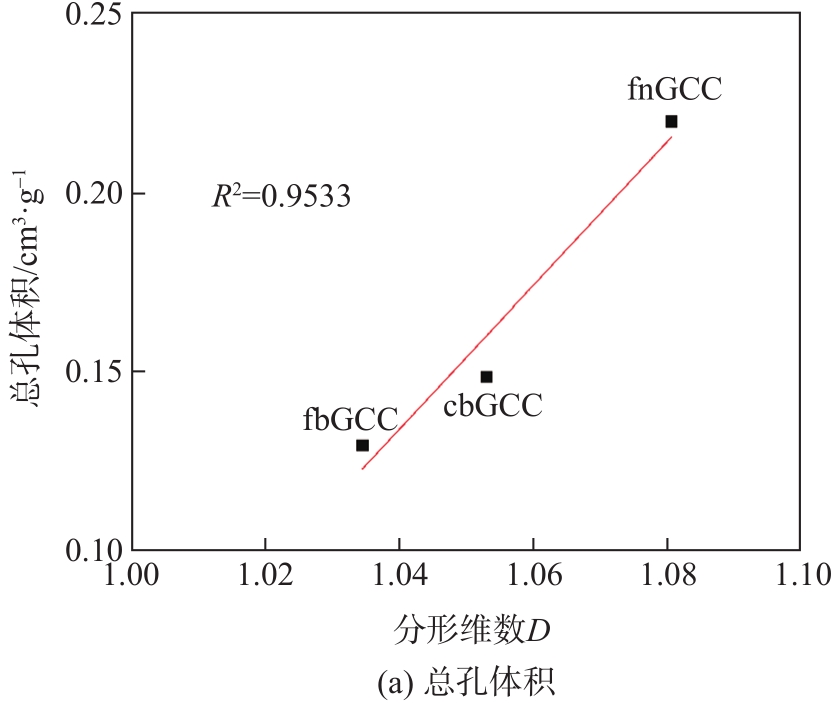
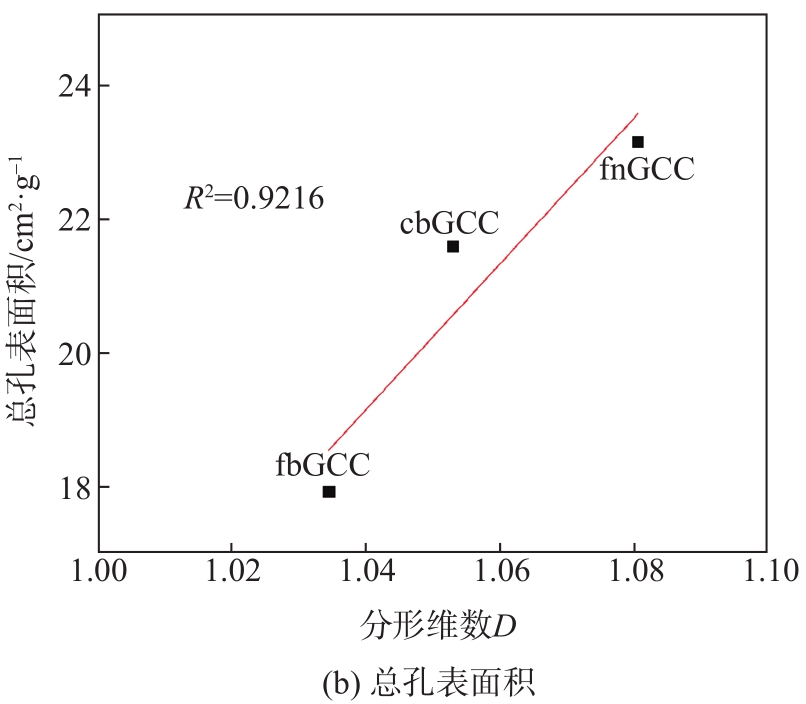
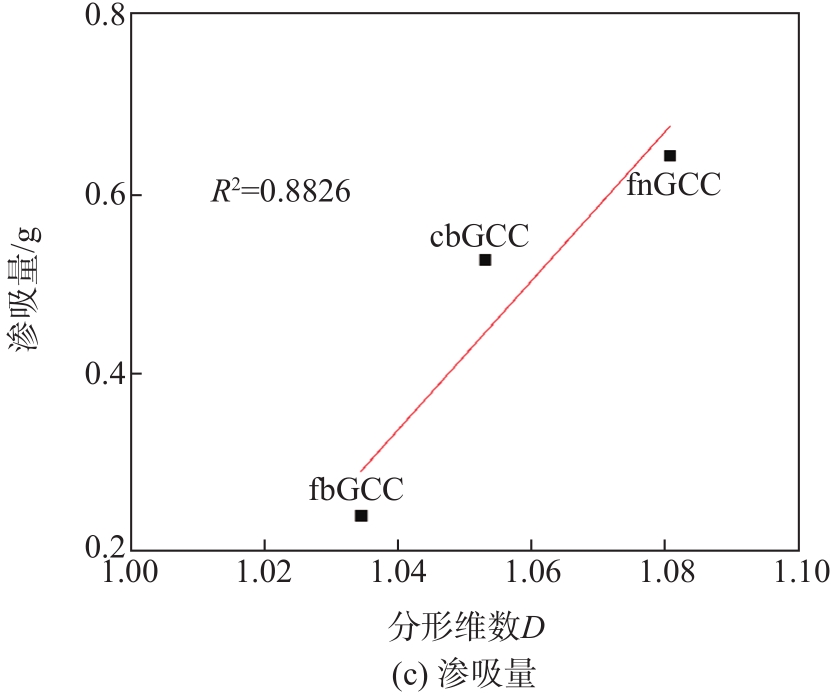
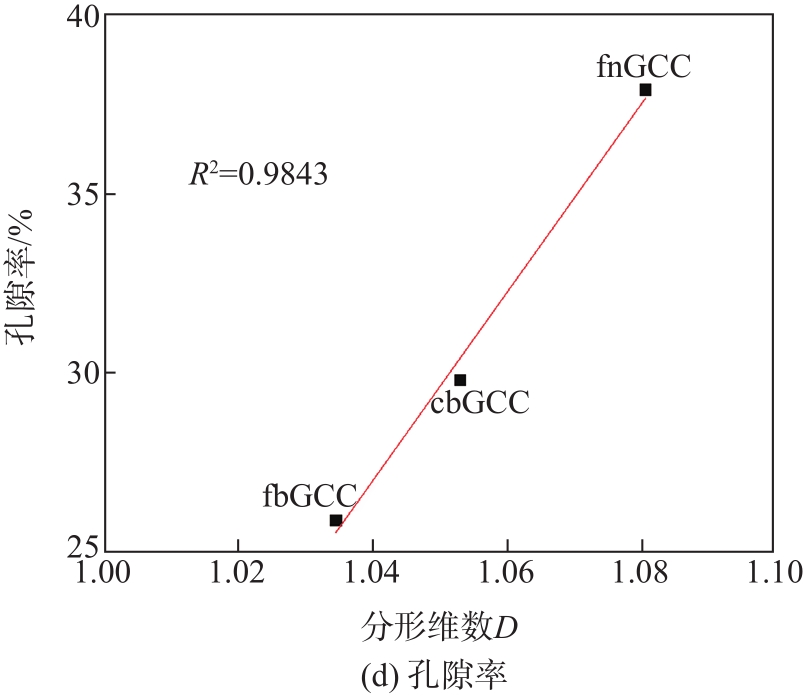
图9 GCC颜料分形维数与孔隙结构的关系

Fig. 9 Relationship between fractal dimension and pore structure of GCC pigments

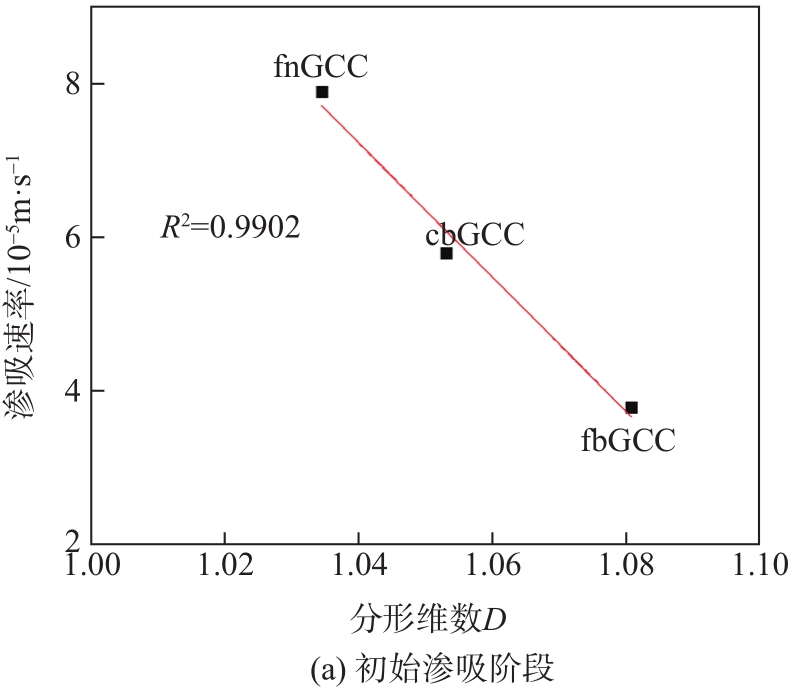
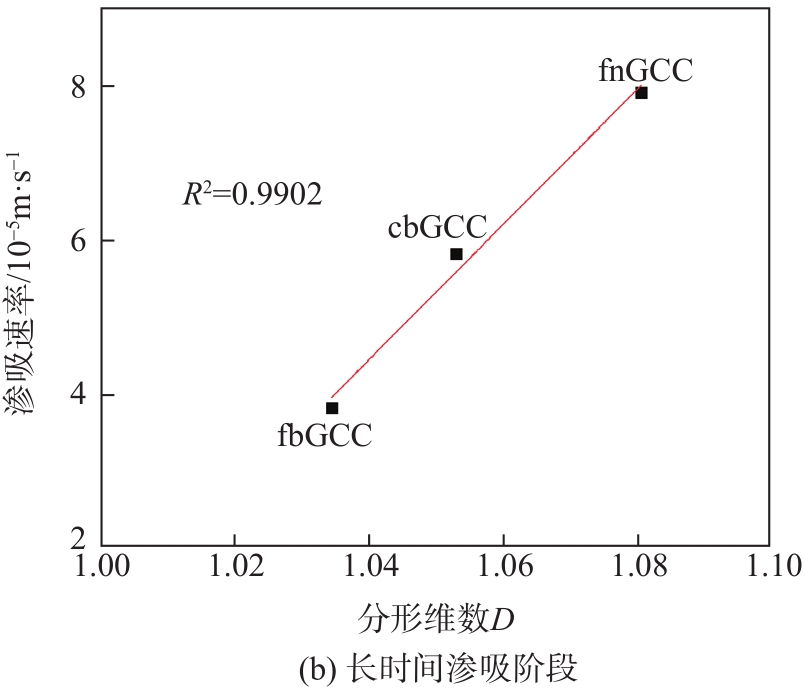
图10 GCC颜料分形维数与渗吸特性的关系

Fig. 10 Relationship between fractal dimension and imbibition characteristics of GCC pigments

从图9可知，cbGCC、fbGCC和fnGCC的孔隙分形维数依次增加，即从结构上的复杂性来说，其结构复杂性依次增加，因此形成了更加复杂的孔隙结构，导致孔隙的累积体积、孔面积、孔隙率相应增加，测量颜料孔隙率及渗吸的孔体积也是随着分形维数的增加而增加。由于孔体积、孔面积、孔隙率随着分形维数的增大而增大，进而使得渗吸质量也随着分形维数的增加而增加。在统一的渗吸测量时间范围内，使得整体渗吸速率必然随着分形维数的增加而增加，形成的整体渗吸速率为： $v_{f n G C C}$ > $v_{c b G C C}$ > $v_{f b G C C}$ ，该结果与渗吸测量的结果一致（见图3）。

针对渗吸初期的情况，渗吸率与分形维数呈负相关，随着分形维数的增加，渗吸率减少，这是由于分形维数大的样本具有复杂、无序的孔隙结构，形成较大的等效毛细管半径，根据渗吸的惯性力机制，毛细管半径越大，多孔介质的渗吸率越少；同时在后期的渗吸过程中，基于L-W渗吸机制，随着毛细管半径增大，多孔介质的渗吸速率增加，也说明了分形维数能够反映渗吸过程的初期渗吸和后期渗吸速率变化规律。所以GCC颜料的分形维数可以较好地反映孔隙结构特征和渗吸特性。

4.4　GCC颜料渗吸特性与分形模型的匹配及修正

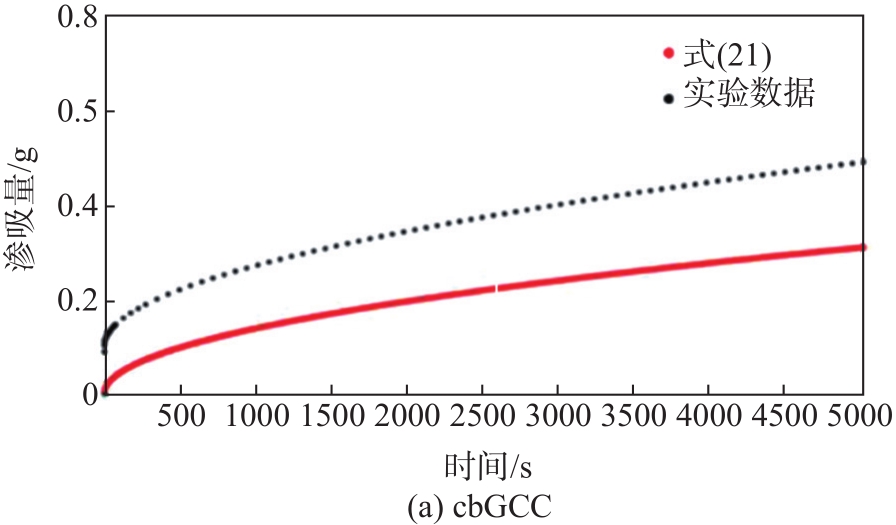
上述分析说明了GCC颜料分形结构与孔结构特征、渗吸特性的确定关系。针对经典渗吸模型与实验渗吸的差距，进行建立的渗吸分形模型（式(21)）的建立与实验渗吸的匹配，参数 $σ$ 、 $ρ$ 、 $μ$ 和 $θ$ 取值见表1。孔隙率 $φ$ 和 $λ_{m a x}$ 可通过压汞实验数据获取。横截面积 $A_{f}$ 取1.44 cm²，模型与实验匹配结果见图11。

图11 渗吸模型与实验结果匹配

Fig. 11 Imbibiition model matches experimental results

从图11可以看出，GCC颜料分形模型预测的渗吸特性与实验渗吸结果仍然有一定差距，没有完全重合。但整体情况要比没有考虑分形结构因素的Bosanquet渗吸模型好的多，渗吸规律的变化程度和趋势与实验渗吸较为一致。造成未重合的主要原因可能是由于本研究中分形维数只是在一定尺度范围的分形结构，并不是多孔介质孔隙全尺度范围内的分形结构，因此不能一致的匹配实验渗吸。在匹配规律趋势基本一致、不能完全重合的情况下，通过使用修正因子^[

24-26]来进一步修改模型，使得模型的结果能够与实验结果达到更高的匹配度。

针对分形模型的渗吸规律与实验渗吸距离差，需要从模型的整体性上引入修正因子，即渗吸量修正因子B来减少模型的预测和实验值之间的总体差距，使得模型渗吸和实验渗吸的起点尽量重合，因此修正后的分形渗吸模型如式(22)所示。

M = \sqrt[]{t \cdot \frac{σ \cdot c o s θ (2 - D_{f}) {(A_{f} φ ρ)}^{2} λ_{m a x}}{4 μ (3 - D_{f}) (1 - φ)}} + B

（22）

通过将B的数值设置在0.08~0.15，进行渗吸初期与实验值的匹配，得到较为理想的结果，其中B_fbGCC = 0.085，B_cbGCC = 0.12，B_fnGCC= 0.14，见图12。

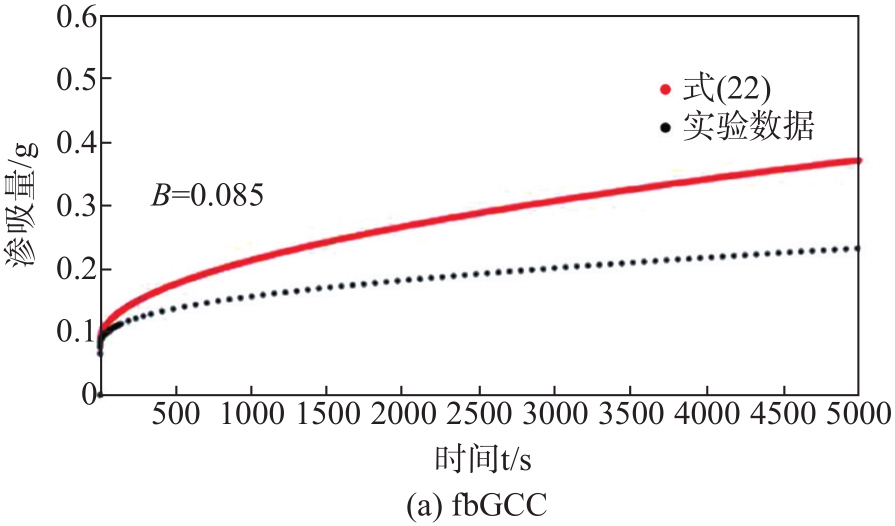
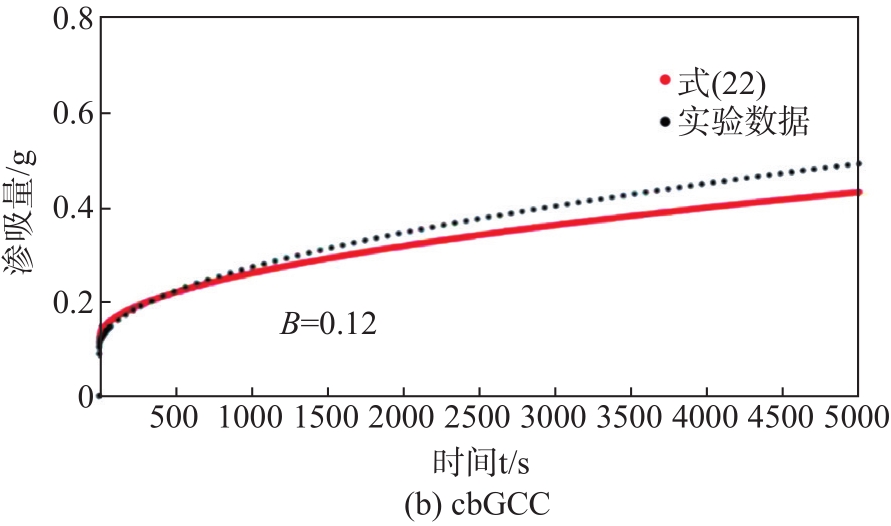
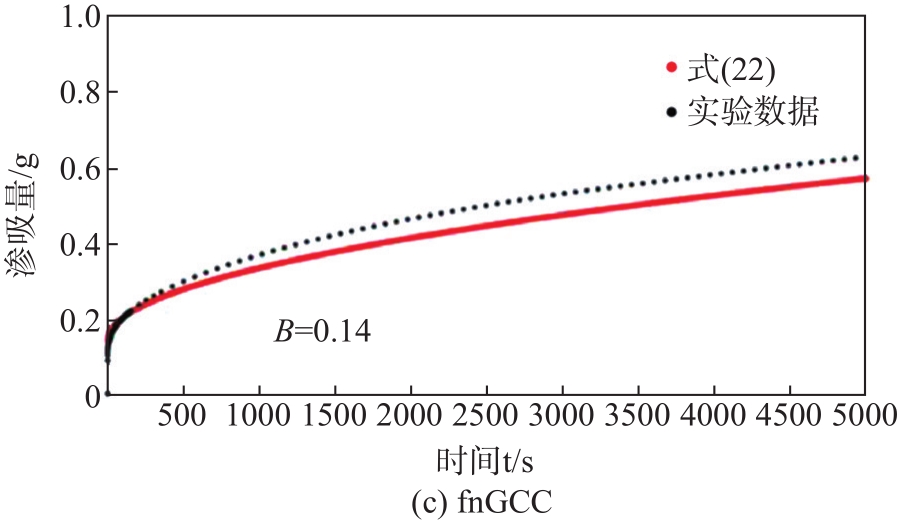
图12 引入修正因子B后渗吸模型与实验结果匹配

Fig. 12 Imbibiition model introducing the modified factor B matches experimental results

在引入修正因子B后，解决了模型与初始渗吸量匹配的问题，但仍有需要进一步修正预测模型渗吸的变化规律，从数学建模角度来讲，在渗吸初期匹配情况下，要改变预测渗吸模型变化形状，需在式(22)中的第一部分引入形状因子K，因此修正后的分形渗吸模型如式(23)所示。

M = \sqrt[]{K t \cdot \frac{σ \cdot c o s θ (2 - D_{f}) {(A_{f} φ ρ)}^{2} λ_{m a x}}{4 μ (3 - D_{f}) (1 - φ)}} + B

（23）

从图2可以看出，后期实际渗吸量和模型预测渗吸量的差距并不是很大，因此对K值在0~2的范围任意取值，经过模拟匹配，实现典型的匹配结果如图13所示。

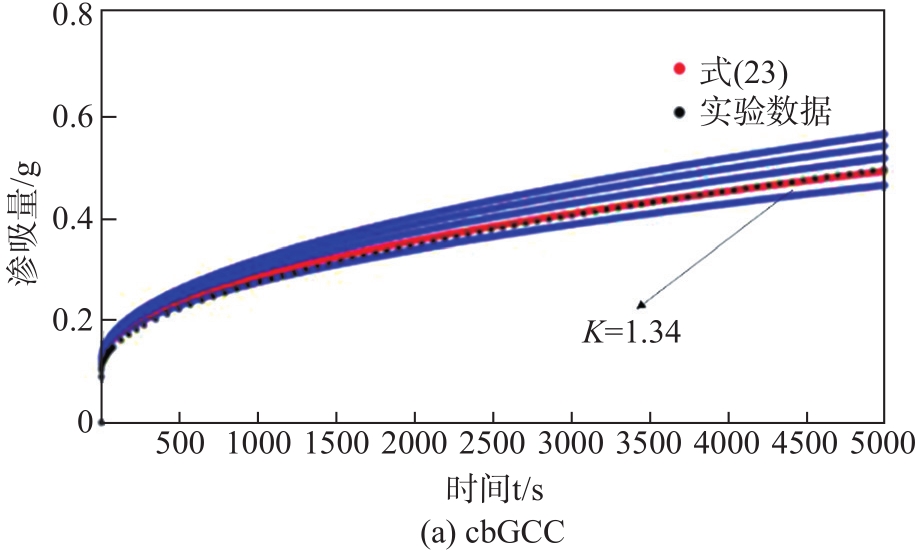
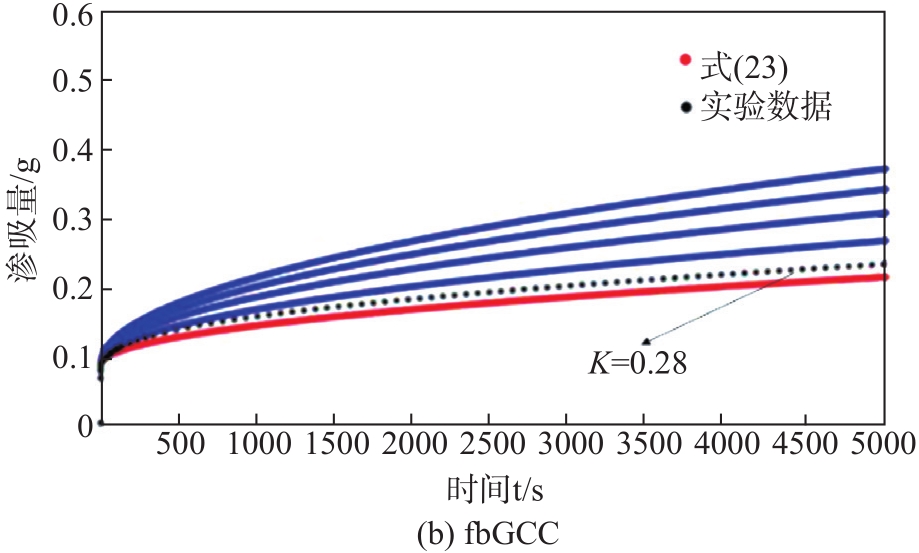
图13 引入形状因子K后渗吸模型与实验结果匹配

Fig. 13 Imbibiition model introducing the shape factor K matches experimental results

从图13可以看出，在上述修正因子B的基础上，cbGCC、fbGCC、fnGCC修正因子K分别等于1.34、0.28、1.38，就可以完成预测模型与实验渗吸完整的匹配。因此考虑了多孔介质渗吸动力学和分形特征因素，建立的分形理论渗吸模型与实验渗吸的预测仍有一定的差异，需要通过修正因子进一步从数学的角度上修改模型，使得模型与预测值达到一致。

5 结　论

本研究以纸张涂层材料的渗吸特性为研究对象，对GCC颜料渗吸特性进行了测量和表征，分析了GCC颜料渗吸特性。在渗吸动力学的基础上，引入多孔介质的分形结构因素建立了GCC颜料渗吸的分形模型，在引入渗吸量修正因子和形状因子情况下，对分形模型进一步修正，对修正后的渗吸分形模型与测量的GCC颜料全过程的渗吸特性进行了匹配，验证了构建模型的准确性。

5.1　GCC颜料的渗吸特性，在渗吸的时间机制下，渗吸量在初期与时间标度成线性变化的关系，与纯惯性力渗吸机制一致。在渗吸的根时间（ $\sqrt[]{t}$ ）标度下，渗吸的后期表现为毛细力支配下的L-W机制。综合两者，GCC颜料渗吸前期和后期的渗吸特性与Bosanquet模型描述的渗吸机制是一致的。

5.2　GCC颜料孔结构分形维数与材料结构的累积体积、孔面积、孔隙率有确定的线性关系。孔体积、孔面积随着分形维数的增大而增大，进而使得渗吸的质量也随着分形维数的增加而增加。针对渗吸初期的情况，渗吸速率与分形维数呈现负相关，说明渗吸初期的惯性力机制；同时在后期的渗吸过程中，渗吸速率与分形维数呈现正相关，也间接说明渗吸后期的L-W机制，因此GCC颜料的分形维数可以较好地反映孔隙结构特征和渗吸特性。

5.3　虽然实验渗吸的前期和后期特性与Bosanquet模型的定性描述是一致的，但是利用Bosanquet模型与实验渗吸的定量匹配中，仍然有一定差距，没有考虑结构的分形特征是匹配差距的潜在原因之一。

5.4　在渗吸动力学支配下，引入多孔材料结构的分形模型在GCC颜料全过程渗吸的匹配中有所提高。在引入渗吸量修正因子和形状修正因子基础上，对渗吸分形模型进行修正，能够匹配GCC颜料全过程的渗吸特性。

参考文献

马凤秋. 不同颜料涂布纸的涂层结构与印刷特性［D］. 天津：天津科技大学， 2008. [百度学术]

MA F Q. Coating Structure and Printing Performance of Different Pigment Coated Paper［D］. Tianjin： Tianjin University of Science & Technology， 2008. [百度学术]

齐晓堃. 印刷适性及材料［M］. 北京：印刷工业出版社， 2007： 46-52. [百度学术]

Qi X K. Printability and Materials［M］. Beijing： Printing Industry Press， 2007： 46-52. [百度学术]

LIU G D， FU S J， LU Z Q， et al. Contrasting Liquid Imbibition Into Uncoated Versus Pigment Coated Paper Enables a Description of Imbibition into New-Generation Surface-Filled Paper［J］. The European Physical Journal E， 2017， 40（12）： 111-121. [百度学术]

陈　港，方志强，黄　婷，等. 涂料主要组分对涂布纸抗液体渗透性能的影响［J］.中国造纸学报， 2008，23（2）： 85-90. [百度学术]

CHEN G， FANG Z Q， HUANG T， et al. The Influence of Main Components of Coating Color on Penetration- Resistance of Coating Paper［J］. Transactions of China Pulp and Paper， 2008， 23（2）： 85-90. [百度学术]

Lucas R. Rate of Capillary Ascension of Liquids［J］. Kolloid-Zeitschrift， 1918， 23（15）： 15-22. [百度学术]

Brú A， Pastor J M. Experimental Characterization of Hydration and Pinning in Bentonite Clay， A Swelling， Heterogeneous， Porous Medium［J］. Geoderma， 2006， 134（3/4）： 295-305. [百度学术]

Schoelkopf J， Gane P， Ridgway C J， et al. Practical Observation of Deviation from Lucas Washburn Scaling in Porous Media［J］. Colloids & Surfaces A Physicochemical & Engineering Aspects， 2002， 206（1）： 445-454. [百度学术]

Ridgway C J， Gane P， Schoelkopf J. Modified Calcium Carbonate Coatings with Rapid Absorption and Extensive Liquid Uptake Capacity［J］. Colloids & Surfaces A Physicochemical & Engineering Aspects， 2004， 236（1/3）：91-102. [百度学术]

Quéré D. Wetting and Roughness［J］. Annual Review of Materials Research， 2008， 38： 71-99. [百度学术]

刘国栋. 造纸涂层材料自渗吸行为机制及理论建模研究［D］. 西安：陕西科技大学， 2014. [百度学术]

LIU G D. Behavior Mechanism and Theoretical Modeling of Spontaneous Imbibition of Paper-Based Coating Materials［D］. Xi'an： Shaanxi University of Science & Technology， 2014. [百度学术]

蔡建超，郁伯铭. 多孔介质自发渗吸研究进展［J］. 力学进展， 2012， 42（6）：735-735. [百度学术]

CAI J C， YU B M. Advances in Studies of Spontaneous Imbibitions in Porous Media［J］. Advances in Mechanics， 2012， 42（6）：735-735. [百度学术]

张　恒，陈克复，陈海峰. 分形理论在纸张涂料与涂层结构研究中的应用［J］. 中国造纸学报， 2002，17（2）： 123-125. [百度学术]

ZHANG H， CHEN K F， CHEN H F. Fractal Theory and Its Application in Paper Coating and Coating Structure Studies［J］. Transactions of China Pulp and Paper， 2002， 17（2）： 123-125. [百度学术]

LIU G D， LU Z Q， ZHANG M Y， et al. The Fractal Characteristic of Porous Coatings Prepared with Ground Calcium Carbonate［J］. Nordic Pulp & Paper Research Journal， 2016，31（4）： 668-675. [百度学术]

LIU G D， ZHANG M Y， Ridgway C， et al. Spontaneous Inertial Imbibition in Porous Media Using a Fractal Representation of Pore Wall Rugosity［J］. Transport in Porous Media， 2014， 104（1）： 231-251. [百度学术]

Gane P， Schoelkopf J， Spielmann D C， et al. Fluid Transport Into Porous Coating Structures： Some Novel Findings［J］. Tappi Journal， 2000， 83 （5）： 77-78. [百度学术]

Gane P， Kettle J P， Matthews G P， et al. Void Space Structure of Compressible Polymer Spheres and Consolidated Calcium Carbonate Paper-coating Formulations［J］. Industrial & Engineering Chemi⁃stry Research， 1996， 35（5）：1753-1764. [百度学术]

Rootare H M， Prenzlow C F. Surface Areas From Mercury Porosimeter Measurements［J］. Journal of Physical Chemistry， 2002， 71（8）：2733-2736. [百度学术]

LI K， ZHAO H. Fractal Prediction Model of Spontaneous Imbibition Rate［J］. Transport in Porous Media， 2012， 91（2）：363-376. [百度学术]

CAI J C， YU B M， ZOU M Q， et al. Fractal Characterization of Spontaneous Co-Current Imbibition in Porous Media［J］. Energy & Fuels， 2010， 24（3）：1860-1867. [百度学术]

YU B M， LI J H. Some Fractal Characters of Porous Media［J］. Fractals， 2001， 9（3）： 365-372. [百度学术]

YU B M， CAI J C， ZOU M Q. On the Physical Properties of Apparent Two-Phase Fractal Porous Media［J］. Vadose Zone Journal， 2009， 8（1）： 177-186. [百度学术]

CAI J， HU X， Standnes D C， et al. An Analytical Model for Spontaneous Imbibition in Fractal Porous Media Including Gravity［J］. Colloids and Surfaces A （Physicochemical and Engineering Aspects）， 2012， 414： 228-233. [百度学术]

LIU G D， ZHANG M Y， Ridgway C， et al. Pore Wall Rugosity： The Role of Extended Wetting Contact Line Length During Spontaneous Liquid Imbibition in Porous Media［J］. Colloids & Surfaces A Physicochemical & Engineering Aspects， 2014， 443： 286-295. [百度学术]

Mason G， Fischer H， Morrow N R， et al. Correlation for the Effect of Fluid Viscosities on Counter-Current Spontaneous Imbibition［J］. Journal of Petroleum Science & Engineering， 2010， 72（1/2）：195-205. [百度学术]

Benavente D， Lock P， Del Cura M Á G， et al. Predicting the Capillary Imbibition of Porous Rocks from Microstructure［J］. Transport in Porous Media， 2002， 49（1）：59-76. [百度学术]

Kazemi H， Gilman J R， Elsharkawy A M. Analytical and Nume⁃rical Solution of Oil Recovery from Fractured Reservoirs with Empirical Transfer Functions［J］. Spe Reservoir Engineering， 1992， 7（2）：219-227. CPP [百度学术]

纸张涂层研磨碳酸钙颜料渗吸特性的分形模型建立及修正

摘要

关键词

1 GCC颜料渗吸特性及孔结构的测量

1.1 实验材料

1.2 渗吸样本的制作及测量

1.3 GCC颜料孔结构的测量