网刊加载中。。。

使用Chrome浏览器效果最佳，继续浏览，你可能不会看到最佳的展示效果，

确定继续浏览么?

复制成功，请在其他浏览器进行阅读

造纸过程成纸质量的单变量统计过程监测研究

- ORCID：
王金咏 ¹
- ORCID：
张凤山 ²
- ORCID：
刘鸿斌 ^1,2,3
✉

1. 南京林业大学林业资源高效加工利用协同创新中心，江苏南京，210037； 2. 山东华泰纸业股份有限公司，山东东营，257335； 3. 广西清洁化制浆造纸与污染控制重点实验室，广西南宁，530004

中图分类号： TS77

最近更新：2021-11-05

DOI：10.11980/j.issn.0254-508X.2021.10.008

摘要

研究了休哈特控制图及其改进方法指数加权滑动均值（EWMA）控制图在造纸行业中的应用。收集了国内某造纸工厂2020年9月10—20日共120批胶版纸生产数据，使用训练集绘制胶版纸定量、厚度、白度、松厚度和表面吸水性的休哈特控制图与EWMA控制图，使用验证集验证控制图的准确性。结果发现，休哈特控制图能够及时监测生产中出现的异常并保证成纸质量，而EWMA控制图的监测标准过于严格，实用性不如休哈特控制图。

关键词

统计过程控制; 控制图; 过程监测; 造纸过程

改革开放以来，我国的制浆造纸产业蓬勃发展，工业生产不断向自动化、规模化方向前进，而实际生产过程中发生故障的几率也随之增大^[

1]。纸张在生产过程中一旦质量波动超出允许范围，就会给企业增加不必要的成本^{[参考文献 2

百度学术}2]。同时，在激烈的行业竞争压力下，产品质量缺乏市场竞争力将对企业的发展产生负面影响^{[参考文献 3

百度学术}3]。因此，精准监测纸张质量是企业需要解决的关键问题。

统计分析法是基于数据驱动的故障监测技术之一，能够提高产品质量和生产稳定性^[

4]。如今，国内外许多造纸企业已经将统计过程模型应用在生产过程质量监测中。统计过程控制的发展经历了单变量统计过程控制和多变量统计过程控制2个阶段^{[参考文献 5

百度学术}5]。单变量统计过程控制是对生产过程中一些关键变量单独地进行统计，为这些指标绘制控制图并监测其波动情况。人们可以根据生产控制的目的和统计原理设置控制限，如果数据点超出控制限，则认为该生产过程不可控^{[参考文献 6

百度学术}6]。单变量统计过程控制主要包含休哈特控制图及其改进方法，利用这些方法可以计算并绘制样本的均值、标准差、指数加权滑动均值（EWMA）等信息的波动。休哈特控制图已经在许多领域得到推广使用^{[参考文献 7

百度学术}7]。

本文着重介绍了单变量统计过程控制在胶版纸造纸过程中纸张定量、厚度、白度、松厚度和表面吸水性控制的方法。首先，对采集到的数据进行正态分析检验，然后使用均值-移动极差-标准差控制图和过程能力图对造纸过程某些重要指标进行可控性分析，最后使用休哈特控制图及其改进方法，建立胶版纸造纸过程中重要指标的实时放行标准，达到生产过程在线监控的目的^[

8]。

1 单变量统计过程控制简介

1.1　正态分析

利用单变量统计过程控制进行质量控制的核心是对产品进行适当分组抽样后进行质量数据分析，正态分布是其中最为关键的工具。因为产品的质量数据通常遵循正态分布或近似正态分布。因此，在使用控制图和分析过程能力时，质量数据也要求以遵循正态分布为前提。当数据略微偏离正态分布时，不会对控制图的结果产生较大的影响。

在质量数据是非正态分布的情况下，直接按照正态数据的处理方法进行过程能力分析和控制图的描绘会有很大的误差。通常，处理非正态数据可以通过Box-Cox变换、Johnson变换等方法，但Box-Cox变换方法对样本数据有严格的要求，不如Johnson变换的条件宽松。因此，本文采用Johnson变换法处理非正态数据，其一般形式如式（1）所示^[

9]。

Z = γ + δ g (\frac{X - ξ}{λ})

（1）

式中，Z为标准正态分布变量；X为非正态分布变量；γ、δ为决定X的分布形状的变量，δ＞0；g(x)为变换函数；ξ为位置参数；λ为尺度参数，λ＞0。

1.2　可控性分析

本文采用均值-移动极差-标准差控制图来分析胶版纸造纸过程中关键指标的可控性。其中，均值控制图可以显示成纸过程中心是否处于受控状态，同时可以消除控制限中异常的子组内分量，跟踪过程位置。移动极差控制图可以显示样本子组间差异是否处于受控状态，并使用移动极差标绘子组平均值以消除子组内变异，利用此图可以使用异常的子组间分量来追踪过程变异。标准差控制图可以显示子组内差异是否处于受控状态，使用异常的子组内分量来标绘过程变异^[

10]。

1.3　过程能力分析

过程能力是指在过程加工上满足加工质量的能力，用来衡量过程加工的内在一致性，通常用过程能力指数C_P或C_PK来描述。当公差中心M和分布中心μ重合时使用C_P描述，用来反映过程能力满足质量要求的程度。而当二者不重合时则使用C_PK描述，用来反映产品质量数据的平均值偏离目标值的过程能力。过程能力指数C_P计算公式如式（2）所示^[

11]。

C_{P} = \frac{技 术 要 求}{过 程 能 力} = \frac{T_{μ} - T_{τ}}{6 σ}

（2）

式中，T_μ、T_τ为规范上、下限；σ为总体标准差。过程能力指标评价^[

12]见表1。

表1 过程能力指数评价表

Table 1 Evaluation of process capability indices

序号	级别	特征值	评价等级	控制建议
1	A++级	C_PK≥2.00	特优	可以考虑成本的降低
2	A+级	2.00≥C_PK≥1.67	优	应当继续保持
3	A级	1.67≥C_PK≥1.33	良	状态稳定，能力良好，应尽力提升到
4	B级	1.33≥C_PK≥1.00	一般	状态一般，控制因素稍有变异就会产生不良影响，应尽力提升为A级
5	C级	1.00≥C_PK≥0.67	差	必须提升过程能力
6	D级	C_PK≤0.67	不可接受	考虑重新整改过程

1.4　休哈特控制图

设某个过程指标数据服从正态分布，在某一时间抽取容量为n的样本，共抽取了k个。根据3 $σ$ 原理， $\bar{x}$ 图的控制限计算方法如式（3）～式（5）所示^[

13]。

U C L_{\bar{x}} = \overset{̿}{x} + 3 σ = \overset{̿}{x} + 3 \frac{\bar{S}}{c_{4} \sqrt[]{n}} = \overset{̿}{x} + A_{3} \bar{S}

（3）

C L_{\bar{x}} = \overset{̿}{x}

（4）

L C L_{\bar{x}} = \overset{̿}{x} - 3 σ = \overset{̿}{x} - 3 \frac{\bar{S}}{c_{4} \sqrt[]{n}} = \overset{̿}{x} - A_{3} \bar{S}

（5）

式中， $U C L_{\bar{x}}$ 、 $L C L_{\bar{x}}$ 为控制上、下限； $C L_{\bar{x}}$ 为中心线； $σ$ 为总体标准差； $\overset{̿}{x}$ 为子组样本均值的均值； $\bar{S}$ 为子组样本标准差的均值；n为子组的样本容量；c₄为与n有关的常数；A₃为控制系数。

S图的控制限计算方法如式（6）～式（8）所示。

U C L_{S} = \bar{S} + 3 σ = (1 + 3 \frac{c_{5}}{c_{4}}) \bar{S} = B_{4} \bar{S}

（6）

C L_{S} = \bar{S}

（7）

L C L_{S} = \bar{S} - 3 σ = (1 - 3 \frac{c_{5}}{c_{4}}) \bar{S} = B_{3} \bar{S}

（8）

式中，UCL_S、LCL_S为控制上、下限；CL_S为中心线；σ为总体标准差； $\bar{S}$ 为子组样本标准差的均值；c₄、c₅为与n有关的常数；B₃、B₄为控制系数。

1.5　EWMA控制图

使用EWMA控制图的优点是可以监控质量指标的指数加权移动平均值，检测过程平均值的微小偏差，同时可以去除样本数据中的较大值和较小值所带来的不利影响。

EWMA控制图的统计量见式（9）^[

14]。

Z_{t} = λ y_{t} + (1 - λ) Z_{t - 1}, t = 1,2, \dots, n

（9）

式中，Z_t为第t个统计量；Z_t-1为第t-1个统计量；y_t为第t个样本值；t为样本序号；n为样本容量；λ为平滑系数（通常取0.2～0.3）。

EWMA控制图的方差统计量见式（10）。

{σ_{Z_{t}}}^{2} = σ^{2} (\frac{λ}{2 - λ}) [1 - {(1 - λ)}^{2 t}]

（10）

式中， $σ_{Z_{t}}$ 为 $Z_{t}$ 的标准差；σ为总体标准差。

根据休哈特3σ原理，EWMA控制图的控制限计算见式（11）～式（13）^[

15]。

\begin{array}{l} U C L = μ + k σ_{Z_{t}} \\ = μ + k σ \sqrt[]{\frac{λ}{(2 - λ)} [1 - {(1 - λ)}^{2 t}]} \end{array}

（11）

C L = μ

（12）

\begin{array}{l} L C L = μ - k σ_{Z_{t}} \\ = μ - k σ \sqrt[]{\frac{λ}{(2 - λ)} [1 - {(1 - λ)}^{2 t}]} \end{array}

（13）

式中，UCL、LCL为控制上、下限；CL为中心线；μ为Z₀；k为控制限参数（通常取3）。

当公式中的t逐渐增大时，（1-λ）²^t会很快收敛到0，控制限的稳定见式（14）～式（15）^[

15]。

U C L = μ + k σ \sqrt[]{\frac{λ}{(2 - λ)}}

（14）

L C L = μ - k σ \sqrt[]{\frac{λ}{(2 - λ)}}

（15）

EWMA控制图不仅考虑到了历史数据的累积作用，而且考虑了当前数据的信息，有一定的预报警能力^[

13]。

2 造纸过程实时放行标准建立

2.1　数据来源和处理

2.1.1　数据来源

实现单变量统计过程控制的关键是利用实际生产中采集的数据建立统计分析模型。本课题训练集样本来自国内某胶版纸生产过程，收集了2020年9月10—20日的历史生产数据，从每天采集到的数据中取10批，共110批历史生产数据作为训练集样本。同时将剩余的10批历史生产数据作为测试集样本。

2.1.2　数据的正态分析结果

对从生产线上采集的训练集样本进行正态性检验。P值是将观察结果认为有效，即具有总体代表性的犯错概率。当P＞0.05时，说明数据呈现正态分布^[

9]。使用Minitab19软件得出纸张定量的P=0.340＞0.05，厚度的P=0.871＞0.05，松厚度的P=0.020，而白度的P＜0.005，表面吸水性的P＜0.005。这说明5个质量指标中只有纸张的定量和厚度服从正态分布，松厚度近似于正态分布，而白度、表面吸水性均不服从正态分布（见图1）。

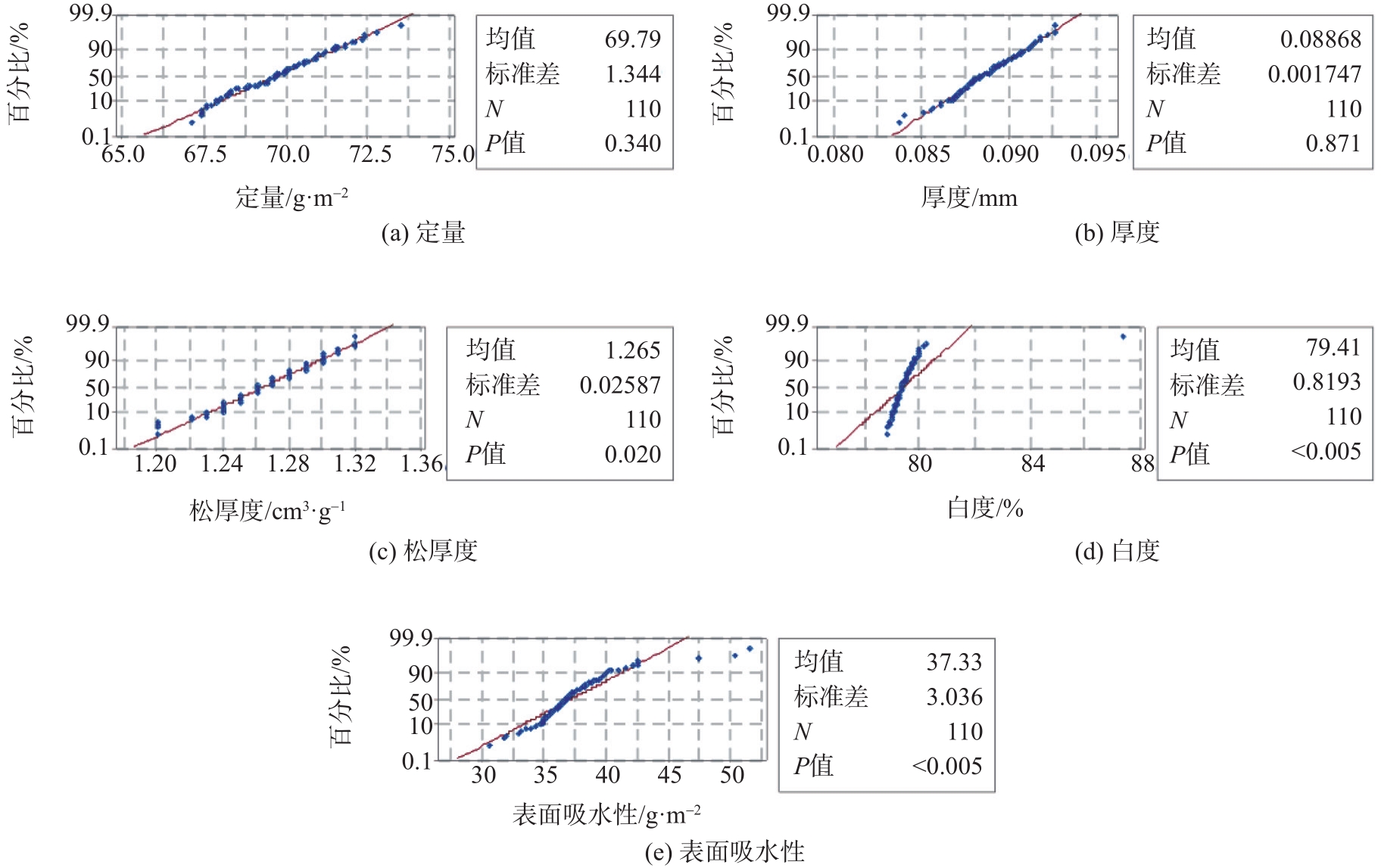
图1 定量、厚度、白度、松厚度和表面吸水性的正态分布图

Fig. 1 Normal probability plots of basic weight, thickness, whiteness, bulk and surface water absorption

对非正态数据进行Johnson变换，如图2和图3所示。从图中可以看出，白度的标准正态分布变量Z=0.74时转换形式最优，根据规则选择S_U曲线，此时P=0.157＞0.05。表面吸水性的标准正态分布变量Z=0.33时转换形式最优，根据规则同样选择S_U曲线，此时P=0.972＞0.05。

图2 白度的Johnson变换

Fig. 2 Johnson transformation of whiteness

图3 表面吸水性的Johnson变换

Fig. 3 Johnson transformation of surface water absorption

2.2　质量指标的可控性分析结果

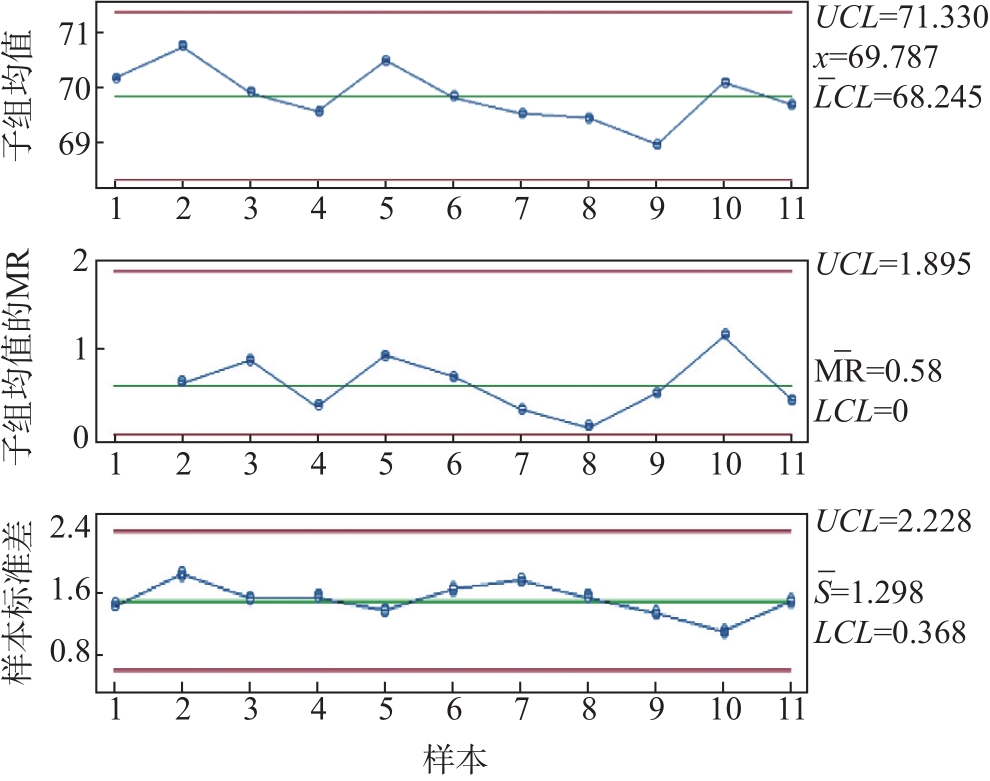
胶版纸造纸过程可控性分析结果见图4～图8。由图4～图8中的单值控制图可以看出，110个胶版纸样本中定量、厚度、松厚度和表面吸水性的平均值均处于受控状态，而白度有1个点超出控制下限，说明此过程不受控制。移动极差控制图说明11个批次胶版纸样本中的定量、厚度、松厚度和表面吸水性批次间差异均处于受控状态，而白度有1个点超出控制上限，说明此过程不受控制。标准差控制图说明每个批次10个样本的定量、厚度、松厚度和表面吸水性均处于受控状态，而白度有1个点超出控制上限，说明此过程不受控制。结果显示胶版纸成纸过程中定量、厚度、松厚度和表面吸水性的可控性较好，白度的可控性较差。

图4 定量的均值-移动极差-标准差控制图

Fig. 4 I-MR-S control chart of basic weight

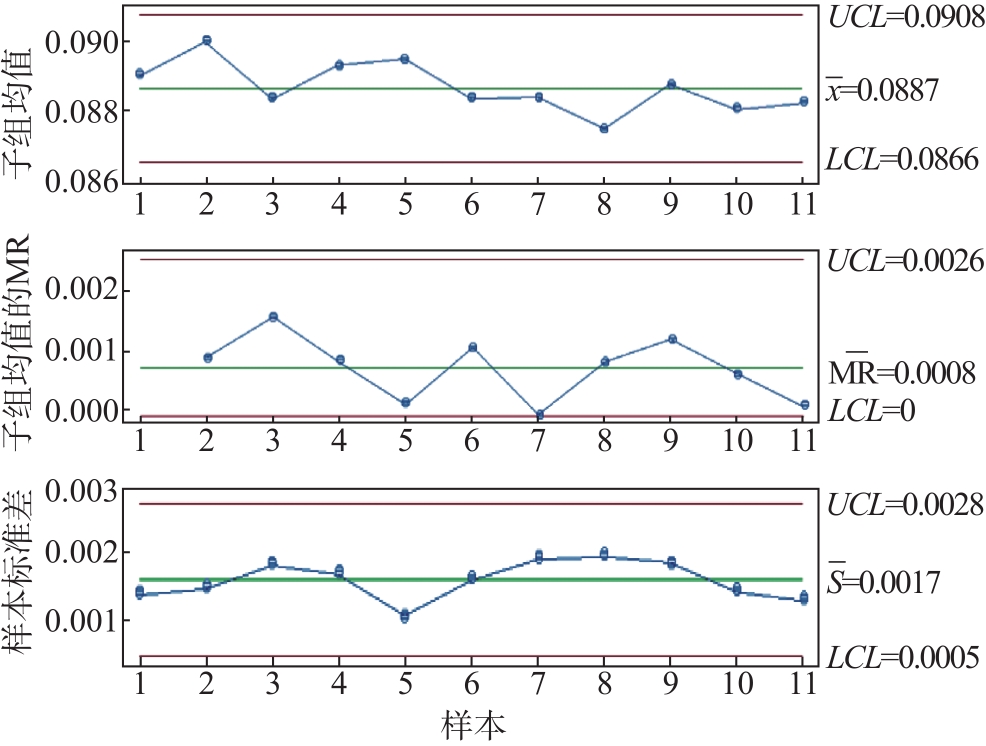
图5 厚度的均值-移动极差-标准差控制图

Fig. 5 I-MR-S control chart of thickness

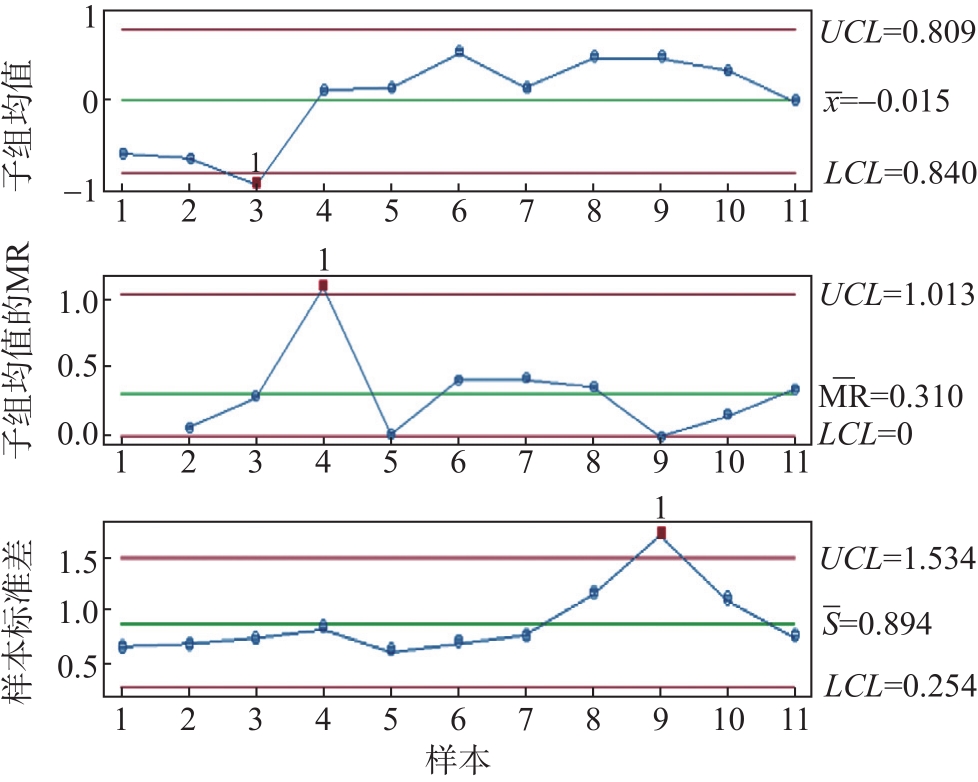
图6 白度的均值-移动极差-标准差控制图

Fig. 6 I-MR-S control chart of whiteness

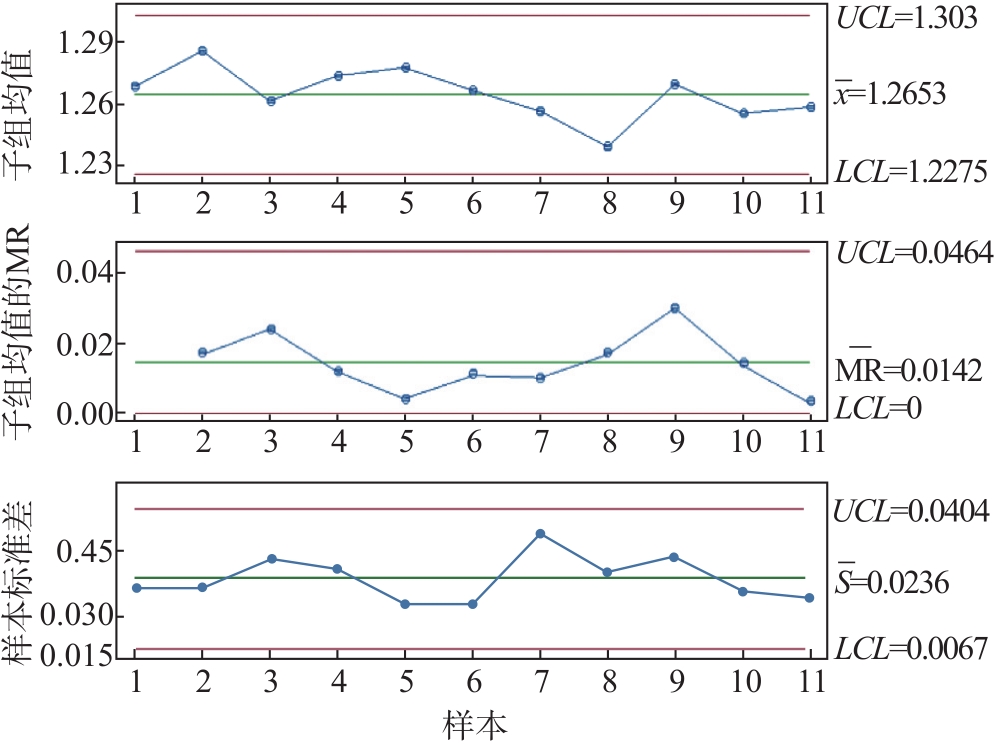
图7 松厚度的均值-移动极差-标准差控制图

Fig.7 I-MR-S control chart of bulk

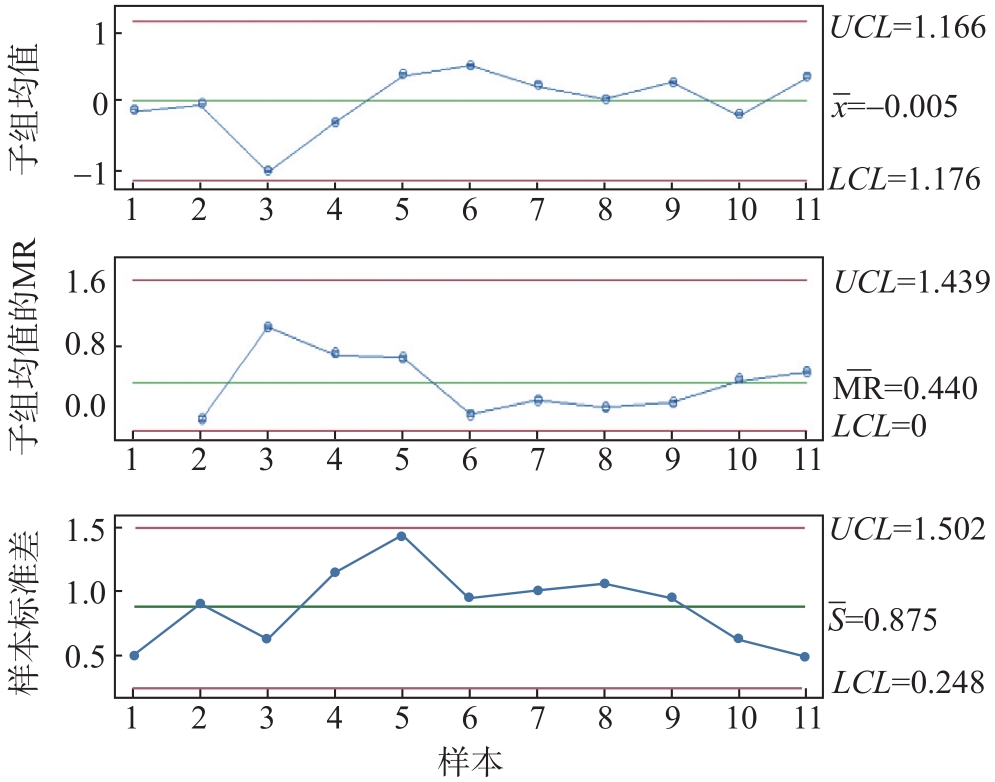
图8 表面吸水性的均值-移动极差-标准差控制图

Fig. 8 I-MR-S control chart of surface water absorption

2.3　质量指标的过程能力分析结果

对胶版纸成纸过程进行过程能力分析，根据国家胶版印刷纸的方法标准和国内某造纸企业规定，70 g胶版纸的质量指标如下：定量（70.0±3.0） g/m²，厚度（0.088±10%）mm，白度（75～85）%，松厚度（1.20～1.34） cm³/g，表面吸水性（20.0～45.0）g/m²。由式（2）计算出质量指标中厚度和白度的C_PK均大于1.33，表示这2个质量指标的过程能力良好，状态稳定。定量、松厚度、表面吸水性的C_PK均小于1.00，表示这3个质量指标的过程能力较差，在生产工艺上仍然有很大的提升空间，企业必须利用各种方法和资源提高过程能力。

2.4　控制图的绘制

2.4.1　休哈特控制图

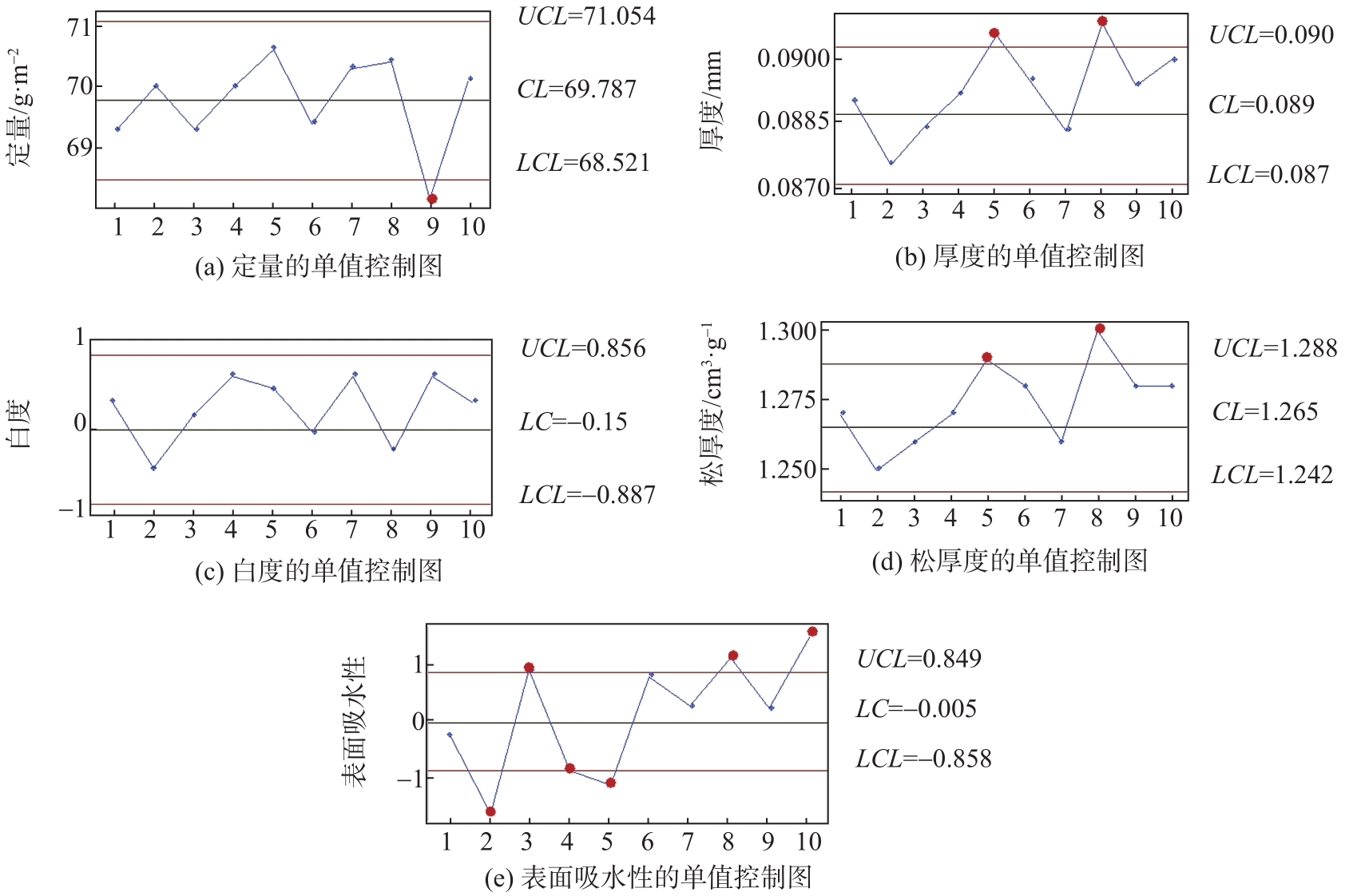
根据采集国内某造纸企业胶版纸成纸数据时选取的子组大小为10，查询国家标准GB/T 4091—2001《常规控制图》得到：A₃=0.975，B₃=0.284，B₄=1.716。按照式（3）～式（5）计算各个质量指标的中心线和上下控制限，结果可得 $\bar{x}$ 控制图控制限UCL、LCL分别为定量71.054、68.521 g/m²，厚度0.090、0.087 mm、白度0.856、-0.887（转换后为79.597%、79.105%），松厚度1.288、1.242 cm³/g、表面吸水性0.849、-0.858（转换后为38.954、35.384 g/m²）。根据采集到的10个批次验证集样本对 $\bar{x}$ 控制图的各个控制限进行验证，判断10个验证集样本的受控情况。10个样本各质量指标的休哈特控制图见图9。

图9 定量、厚度、白度、松厚度和表面吸水性的休哈特控制图

Fig. 9 Shewhart control charts of basic weight, thickness, whiteness, bulk and surface water absorption

从图9中得出1、6、7号样本的成纸过程参数均为正常工艺参数，5个质量指标均在控制限的范围之内。

而9号样品的定量低于LCL，可能是生产过程中各个因素共同作用累积后的结果，比如稀释水量偏大、进浆量偏小、筛板不畅通、卷曲压力波动、浆料纤维发生变化或者化学品性质变化等^[

16]，需要操作人员密切关注生产状态，强化生产操作，当高定量纸种与低定量纸种相互改产时也要做好标识。5、8号样本的厚度、松厚度均高于UCL，从图9还可以看出，5、8号样本的定量也较高，这可能是导致成纸厚度、松厚度均超限的原因。2、4、5号样本的表面吸水性均低于LCL，3、8、10号样本的表面吸水性均高于UCL，表面吸水性与原料纤维的种类、打浆度、成纸水分、压光程度均有很大的关系。纸浆中半纤维素含量较高、打浆度过高、成纸的水分较小等因素会导致浆料中细小纤维增多，使纤维间结合力增大，孔隙率降低，纸张紧度过高，表面吸水性下降；反之则会使表面吸水性上升^{[参考文献 17

百度学术}17]。在实际生产操作中，调节表面吸水性时要考虑到其他物理性能如抗张强度、厚度之间的相互联系和制约关系。

由图9可以看出，正常样本的各个质量指标数据点均在控制限以内，而生产过程出现异常的样本质量指标数据点均有超出上下控制限的情况出现，说明建立的胶版纸成纸过程控制标准能较好地监测成纸质量。

2.4.2　指数加权滑动均值控制图

按照式（9）～式（15）计算训练集中各个质量指标的EWMA统计量和控制限，结果可得，EWMA控制图控制限UCL、LCL分别为定量70.202、69.372 g/m²，厚度0.0892、0.0881 mm、白度为79.670%、79.159%，松厚度1.273、1.258 cm³/g、表面吸水性为38.260、36.409 g/m²。根据采集到的10个批次验证集样本对EWMA控制图的各个控制限进行验证，判断10个验证集样本的受控情况。10个样本各质量指标的EWMA控制图见图10。

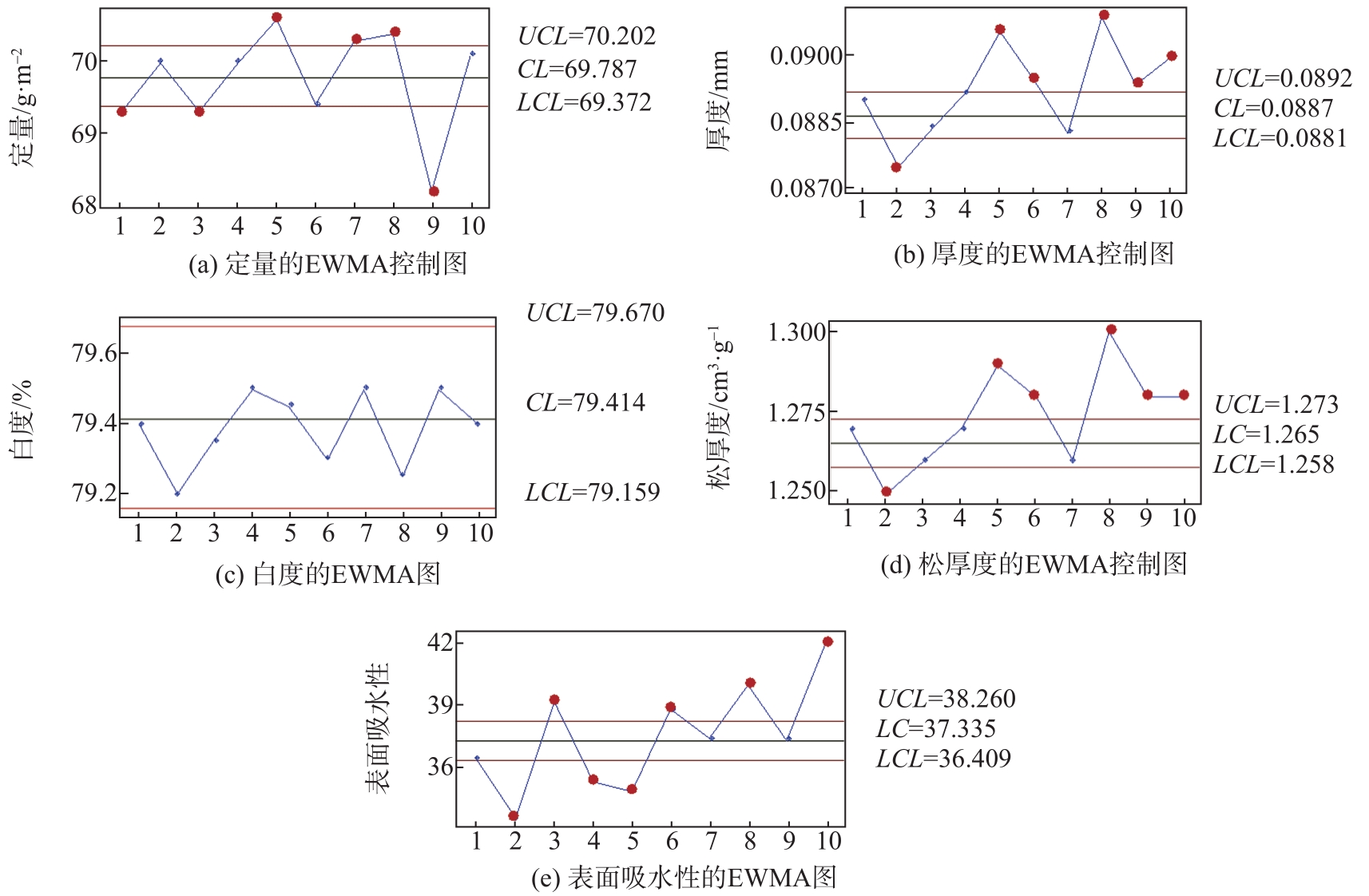
图10 定量、厚度、白度、松厚度和表面吸水性的EWMA控制图

Fig. 10 EWMA control charts of basic weight, thickness, whiteness, bulk and surface water absorption

比较图9和图10，原先显示为正常参数的1、6、7号样本也出现超限的质量指标。在图10上，1、3、9号样本的定量低于LCL，5、7、8号样本定量高于UCL；2号样本的厚度、松厚度均低于LCL，5、6、8、9、10号样本的厚度、松厚度均高于UCL；2、4、5号样本的表面吸水性低于LCL，3、6、8、10号样本的表面吸水性高于UCL。

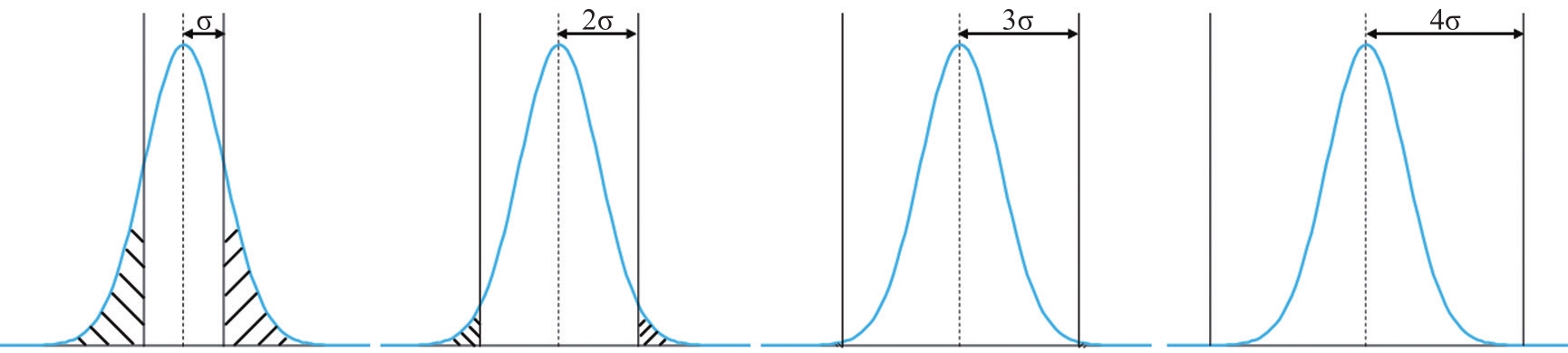
由于EWMA控制图的控制上下限范围小于 $\bar{x}$ 控制图，所以对于小波动更加敏感，显示异常的样本数量也更多。图11为4种控制限所对应的Ⅰ类错误。如图11所示，控制限变窄会导致控制图产生Ⅰ类错误的概率增大，即生产过程正常的情况下，由于数据点超出控制限而判断生产出现异常的错误增多^[

18]。

图11 4种控制限所对应的Ⅰ类错误

Fig. 11 Type Ⅰ error corresponding to the 4 control limits

注曲线代表稳定受控的生产过程；阴影部分代表样品出现在控制限以外的概率。

EWMA控制图的0.5～2个 $σ$ 标准控制条件严格，适用于监测精度很高的过程。而胶版纸生产过程是流程性材料工艺，受随机因素的影响较大，使用EWMA控制图会产生过度控制的情况，所以对于胶版纸的质量指标控制用 $\bar{x}$ 控制图的3 $σ$ 标准就已经足够严格且错误造成损失最小。

3 结　论

本课题按照建立统计模型的步骤，针对胶版纸生产过程定量、厚度、白度、松厚度和表面吸水性这些关键质量指标，根据3 $σ$ 原理建立了休哈特控制图和EWMA控制图，比较二者发现，EWMA控制图对于微小波动敏感性较高。

随着过程控制的发展，国内许多造纸企业已经建立了能够保存大量过程数据的生产过程控制系统。应用单变量统计过控制可以提取出隐藏在数据中的信息并合理应用，这对于提高造纸生产的安全性和成纸质量的稳定性具有重大意义。然而造纸过程工艺复杂、设备庞大，随机因素众多，变量之间的耦合作用较强，传统的单变量统计过控制仅注意监测少量的过程变量，一旦发现问题很难找出根源，如何建立和发展适合造纸生产过程的准确的统计过程模型还需要更深入的研究。

参考文献

刘鸿斌，陈　琴，张　昊，等.废水处理系统的动态过程监测［J］.中国造纸， 2019， 38（2）：46-53. [百度学术]

LIU H B， CHEN Q， ZHANG H， et al. Dynamic Process Monitoring of Wastewater Treatment Systems［J］. China Pulp & Paper， 2019， 38（2）： 46-53. [百度学术]

王龄松，马璞璠，叶凤英，等.造纸废水处理过程微小故障检测方法研究［J］.中国造纸， 2017， 36（8）：20-25. [百度学术]

WANG L S， MA P F， YE F Y， et al. Incipient Fault Detection in Papermaking Wastewater Treatment Processes［J］. China Paper & Pulp， 2017， 36（8）： 20-25. [百度学术]

郭佳文，罗佐帆，黄一峰，等. DCS系统在制浆造纸生产过程中的应用及发展［J］. 大众科技， 2019， 21（12）：22-25. [百度学术]

GUO J W， LUO Z F， HUANG Y F， et al. Application and Development of DCS System in Paper-making Industry［J］. Popular Science & Technology， 2019， 21（12）： 22-25. [百度学术]

李祥宇，杨　冲，宋　留，等. 基于支持向量机的造纸废水处理过程故障诊断［J］. 中国造纸学报， 2018， 33（3）： 55-60. [百度学术]

LI X Y， YANG C， SONG L， et al.Fault Detection of Papermaking Wastewater Treatment Process Based on Independent Component Analysis［J］. Transactions of China Pulp and Paper， 2018， 33（3）： 55-60. [百度学术]

杨　冲，宋　留，刘鸿斌. 基于独立元分析的制浆造纸废水处理过程故障检测［J］. 中国造纸学报， 2019， 34（1）： 66-72. [百度学术]

YANG C， SONG L， LIU H B. Fault Diagnosis of Papermaking Wastewater Treatment Processes Based on Support Vector Machine［J］. Transactions of China Pulp and Paper， 2019， 34（1）： 66-72. [百度学术]

钱夕元，荆建芬，侯旭暹. 统计过程控制（SPC）及其应用研究［J］. 计算机工程， 2004， 30（19）：144-145. [百度学术]

QIAN X Y， JING J F， HOU X X. Research of Statistical Process Control （SPC） and Its Application［J］. Computer Engineering， 2004， 30（19）： 144-145. [百度学术]

田学民，曹玉苹. 统计过程控制的研究现状及展望［J］. 中国石油大学学报（自然科学版）， 2008， 32（5）：175-180. [百度学术]

TIAN X M， CAO Y P. Situation and Perspectives of Statistical Process Control［J］. Journal of China University of Petroleum（Natural Science Edition）， 2008， 32（5）： 175-180. [百度学术]

王永香，李　淼，米慧娟，等. 应用统计过程控制技术研究建立青蒿金银花醇沉过程中实时放行标准［J］. 中草药， 2016， 47（9）：1501-1507. [百度学术]

WANG Y X， LI M， MI H J， et al. Real-time Release Control of Alcohol Precipitation about Artemisiae Annuae Herba and Lonicerae Flosbased on Statistical Process Control Technology［J］. Chinese Traditional and Herbal Drugs， 2016， 47（9）： 1501-1507. [百度学术]

李长江，邓文平，曹元元，等. 基于Box-Cox变换与Johnson变换非正态过程能力分析［J］. 齐齐哈尔大学学报（自然科学版）， 2015， 31（1）：66-70. [百度学术]

LI C J， DENG W P， CAO Y Y， et al. Process Capability Analysis in Non-normality Based on Box-Cox Transformation and Johnson Transformation［J］. Journal of Qiqihar University （Natural Science Edition）， 2015， 31（1）： 66-70. [百度学术]

封　波. 多变量统计过程控制的应用研究［D］. 杭州：浙江大学， 2002. [百度学术]

FENG B. Application Research of Multivariable Statistical Process Control［D］. Hangzhou： Zhejiang University， 2002. [百度学术]

范红杰，周　聪，沈　毅，等. 统计过程控制技术在产品质量控制点中的应用［J］. 林业机械与木工设备， 2014， 42（3）：39-42. [百度学术]

FAN H J， ZHOU C， SHEN Y， et al. Application of Statistical Process Control Technology in Product Quality Control Points［J］. Forestry Machinery & Woodworking Equipment， 2014， 42（3）： 39-42. [百度学术]

陈　波. 浅谈精品的评价与过程能力指数［J］. 中国新技术新产品， 2013， 6（11）：240. [百度学术]

CHEN B.An Introduction to the Evaluation of Excellence and Process Capability Index［J］. China New Technologies and Products， 2013， 6（11）： 240. [百度学术]

周　娟. 制造系统多级质量控制模式与控制图方法研究［D］. 杭州：浙江大学， 2017. [百度学术]

ZHOU J. Research on Multi-level Quality Control Modes and Control Methods for Manufacturing System［D］. Hangzhou： Zhejiang University， 2017. [百度学术]

吴先沛. 锂电池生产线统计过程控制研究与系统设计［D］. 广州：广东工业大学， 2019. [百度学术]

WU X P. Research and System Design of Statistical Process Control Method for Lithium Battery Production Line［D］. Guangzhou： Guangdong University of Technology， 2019. [百度学术]

张　丽. 动态EWMA中位值控制图的理论与应用研究［D］. 秦皇岛：燕山大学， 2014. [百度学术]

ZHANG L. Theory and Application of Dynamic EWMA Control Chart［D］. Qinhuangdao： Yanshan University， 2014. [百度学术]

单文娟，汤　伟，刘　炳.纸张横幅定量多变量解耦控制策略研究［J］.中国造纸学报， 2018， 33（2）：44-50. [百度学术]

SHAN W J， TANG W， LIU B.Multivariable Decoupling Control Strategy for Cross-direction Basis Weight of Papermaking Process［J］. Transactions of China Pulp and Paper， 2018， 33（2）： 44-50. [百度学术]

付丽红，张铭让，齐永钦，等.胶原纤维和植物纤维混合抄片吸水性的研究［J］.中国造纸学报， 2001，16（2）：71-75. [百度学术]

FU L H， ZHANG M R， QI Y Q， et al.Absorptivity of the Compound Sheet Made of the Mixture of Collagen and Cellulose Fibers［J］. Transactions of China Pulp and Paper， 2001，16（2）： 71-75. [百度学术]

庄常陵.控制图犯第Ⅰ/Ⅱ类错误分析［J］.长春师范学院学报， 2001， 20（1）：21-23. [百度学术]

ZHUANG C L. The Ⅰ/Ⅱ Mistake Analysis of Control Chart［J］. Journal of Changchun Norman University， 2001， 20（1）： 21-23. [百度学术]

CPP [百度学术]

造纸过程成纸质量的单变量统计过程监测研究

摘要

关键词

1 单变量统计过程控制简介

1.1 正态分析

1.2 可控性分析

1.3 过程能力分析

1.4 休哈特控制图

1.5 EWMA控制图