摘要
本研究提出了一种基于梯度增强决策树(GBDT)算法的纸张质量软测量模型,该方法可在线软测量纸张的关键物理指标如抗张强度、柔软度和松厚度。结果表明,采用GBDT进行纸张质量软测量时,抗张强度、柔软度和松厚度的平均相对误差分别为7.21%、7.38%和3.5%;采集新数据验证后,纸张抗张强度、柔软度和松厚度的平均相对误差分别为6.87%、6.88%和3.12%,表明模型对新验证数据的预测结果精度高。
产品质量是制造业发展的生命线,是支撑经济转型升级的基石。在造纸企业中,在高产量高车速下纸张生产时引发各种质量问题,如依靠上浆定量对于纸张松厚度的控制,依靠刮刀起皱对于纸张吸水性的控制等变得更加具有挑战性,间接导致产品质量问题日益突出,同时消费者对于纸张质量要求的不断提高也给企业生产带来了巨大挑战。在“中国制造2025”坚持以创新驱动、质量为先、绿色发展、结构优化、人才为本的基本方
目前,造纸企业采取的质检方式为先产后检和抽检两种相结合的方式。其中,先产后检基于仪器质检。该检测方式存在滞后性,不仅会导致产品质量得不到及时的反馈,且生产过程无法实现闭环控制,基于数据驱动模型的优化控制将无法实
影响产品质量的因素有很多,如浆料的纤维形态对纸张质量影响较大,张美娟等
决策树是机器学习中最流行的分类和回归方法之
为解决对造纸企业离线质检工作量大,纸张关键物理指标无法在线实时软测量的问题,本课题利用基于机器学习的数据驱动算法,建立精确的质量在线软测量模型。模型以原料纤维形态数据、浆料配比数据、磨浆工艺参数为初始输入,利用纤维形态软测量模型预测磨后纤维形态数
对纸张抗张强度、柔软度和松厚度进行软测量,主要包括利用磨后纤维形态软测量模
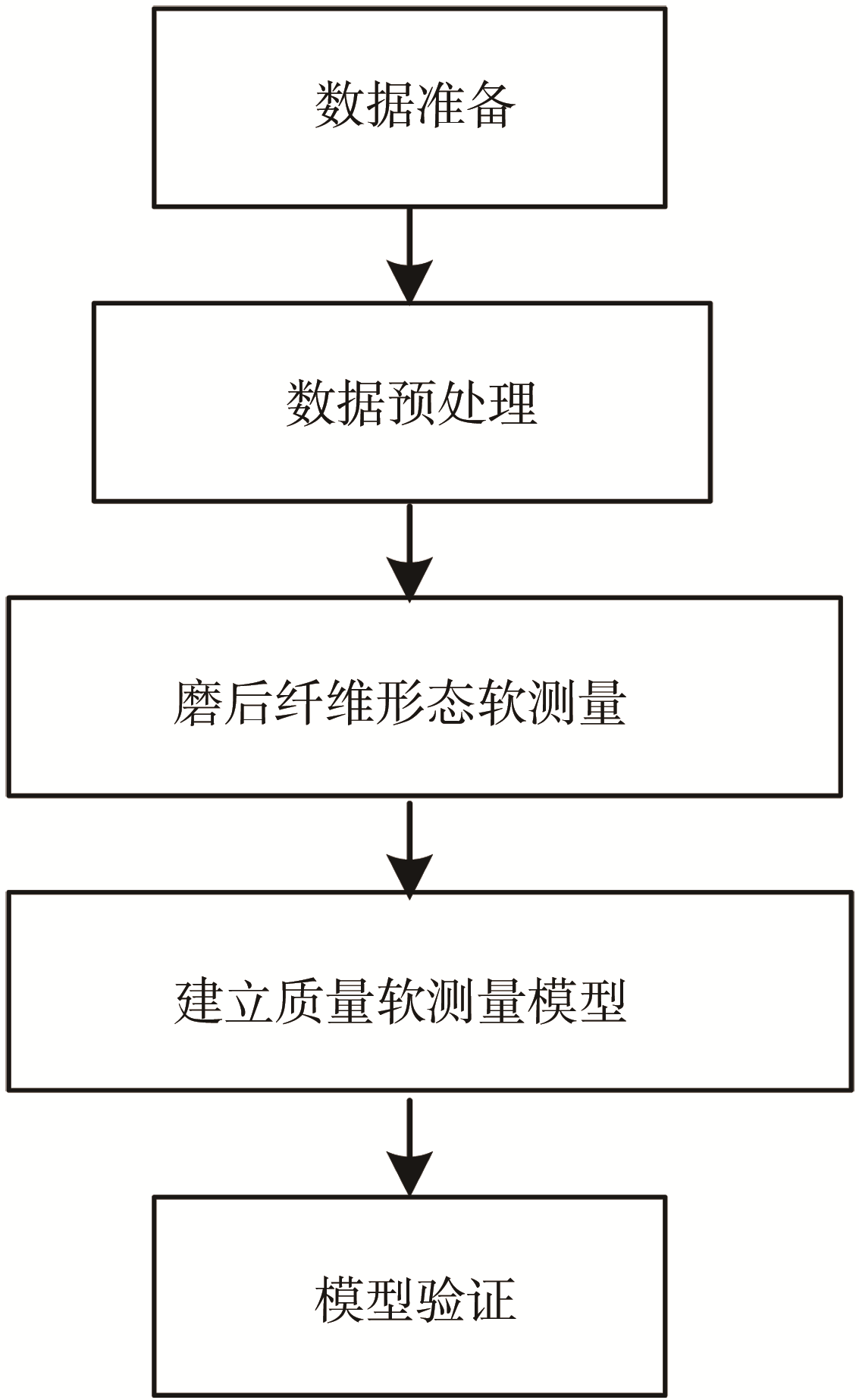
图1 质量软测量模型技术路线图
本研究首先获取某造纸企业实际生产中每轴原纸的浆料配比、质量检测数据(抗张强度、柔软度及松厚度)以及生产周期内的磨浆机工艺数据和纸机工艺数据。然后进行数据的预处理,即先剔除缺失值、恒定值等不真实的数据,再将质检数据与造纸工艺数据匹配。接下来利用磨后纤维形态软测量模
考虑到纸张生产过程中存在间歇性设备(如磨浆机)、间歇性容器(如上浆池),导致其是一个非常复杂的非线性、时延性和不确定性过程,普通的模型难以准确对该过程进行较好拟合。GBDT算法结合了回归树和增强算法框架,通过迭代降低模型的残差,有很强的非线性处理能力和预测能
(1)确定目标函数。首先确定输入变量和输出变量Y。
(2)搜索裂变特征值和裂变点。裂变特征值将待裂变节点分成n个区域空间,对每个区域遍历响应的模型。假设裂变特征j和裂变节点s在二叉搜索中定义一对半平面:和,其中,、为区域空间。因此查找裂变特征j和裂变节点s的目标公式如
| (1) |
式中,为实际输出变量,为拟合输出变量。
(3)为了描述模型的精确程度,引入损失函数(loss function)。假设为训练样本, )代表参数集合,是每棵回归树的权重,是回归树内的参数,因此总体模型函数如
| (2) |
| (3) |
式中,为总体模型函数,为第个基础回归树函数,为回归树棵树,为第棵回归树权重,是第棵回归树内的参数。
(4)为了求得总体模型函数,需解出
| (4) |
| (5) |
式中,为回归树棵树,是第1棵回归树内的参数,为第棵回归树权重,为第个基础回归树函数,为前个模型函数,为前个函数。
GBDT算法采用梯度下降法求极小值,最大下降梯度方向是损失函数在当前模型下的负梯度方向,计算如
| (6) |
计算梯度,最终得到一个n维度下降方向向量(。
然后通过最小二乘法求得的内部参数,循环 和进而求得,带入
本研究采集了某造纸厂实际生产数据作为建模的数据基础(来自企业MES系统数据)。主要包含从业务数据库提取浆料配比数据、磨浆工艺数据及质检数据,采集频率为每轴纸的相关数据,从生产过程数据库提取造纸工艺数据,采集频率为每分钟的相关数据。本研究所展示的数据均为脱敏处理后的数据。
由于在造纸实际过程中,当生产出现停产(如突发断纸)或者停机状态及制造执行系统(MES)网络通信异常时,大部分数据是零值或者空缺值,一些计量仪器还会显示最终时刻的计量值(即出现恒定值异常)。故本研究首先剔除这些非真实有效数据,以提高数据的可利用性,保证不会影响后期数据建模的模型精度。另外对于企业而言,不可能做到对生产的全部原纸产品进行所有质量指标的检测,而是对部分原纸产品轴纸末端采样进行全检和非全检混合的模式。在生产上,生产一轴纸约需1~2 h,针对轴纸末端的检测仅是下轴时刻1 min内的质检指标值,故还要匹配到这1 min内的纸机工艺参数,即根据质检数据中每一轴纸的轴号信息,结合卷纸长度指标,对采样原纸质检数据进行生产时序上的匹配,以完成纸机工艺参数与质检数据的逐一匹配,为后续建模做数据基础。
本研究具体的数据预处理方式如下:对于存在缺失的数据(如磨浆机功率缺失、非全检数据)进行删除;对于工艺参数与质检数据的匹配,首先导出卷纸长度数据,剔除缺失值及恒定值,然后从中提取所有最大值即所有卷纸末端时刻点的卷纸长度值,该时刻点就是质检点时刻,最后匹配上该时刻的纸机工艺参数值,即得到同一时刻上质检数据与工艺数据的完整建模数据。本研究建模数据和验证数据分别采集于某造纸厂2018年4月1日至2018年10月31日和2018年12月15日至2019年2月11日两个时间段内的生产数据,经上述预处理、数据匹配后共计建模有效数据580组64维,验证数有效数据123组64维。
在建立纸张质量软测量模型之前,还需要先通过磨后纤维形态软测量模
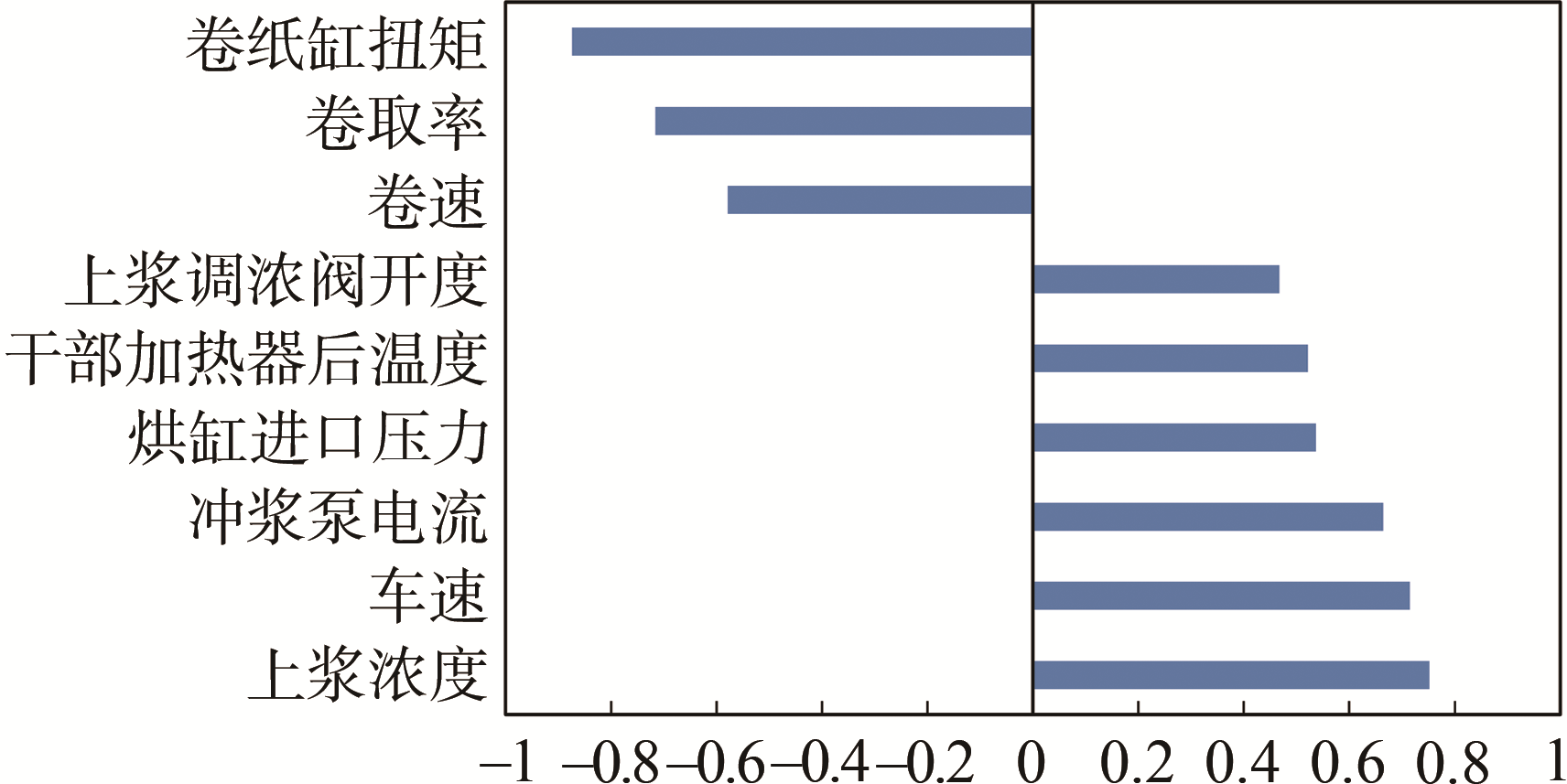
(a) 抗张强度
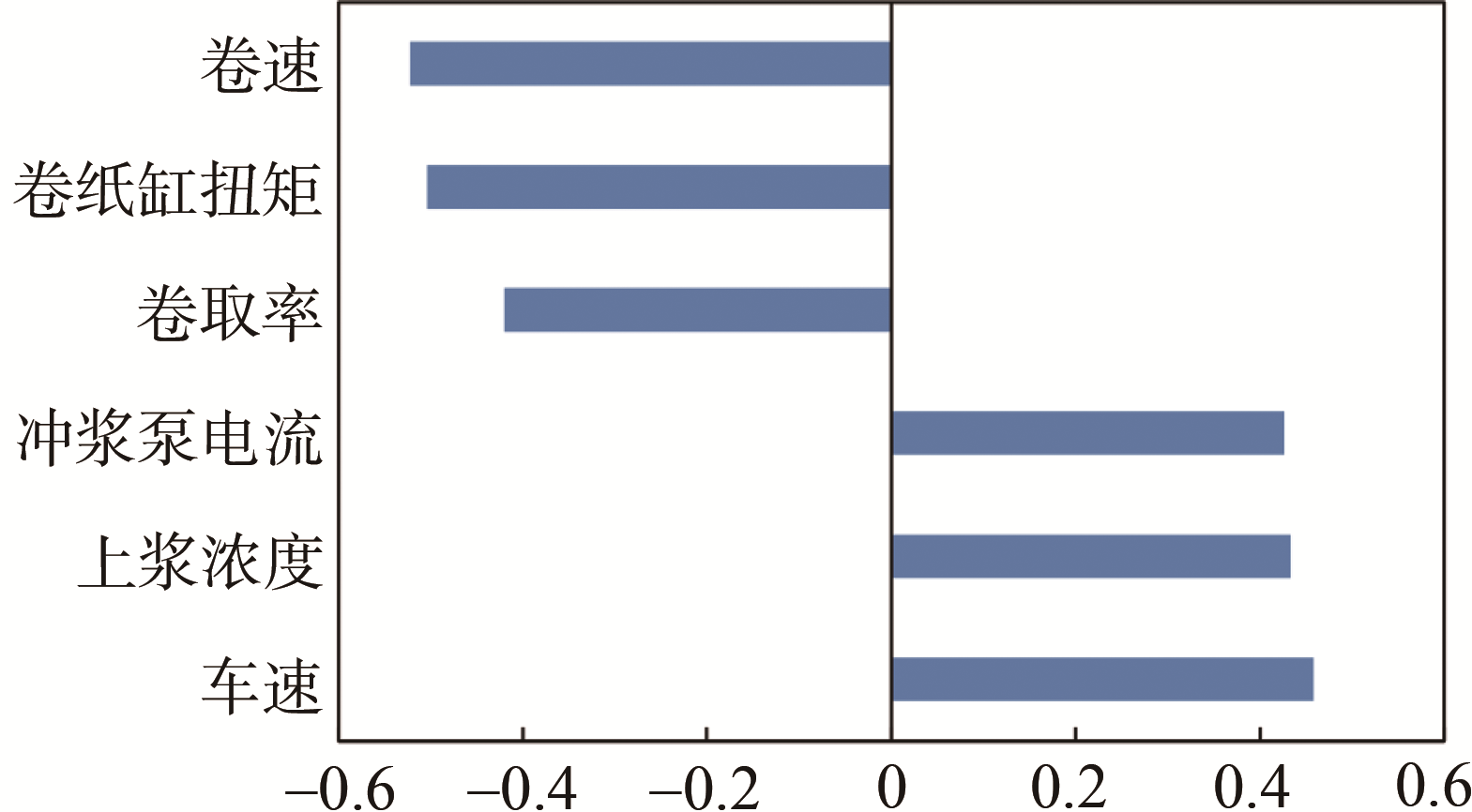
(b) 柔软度
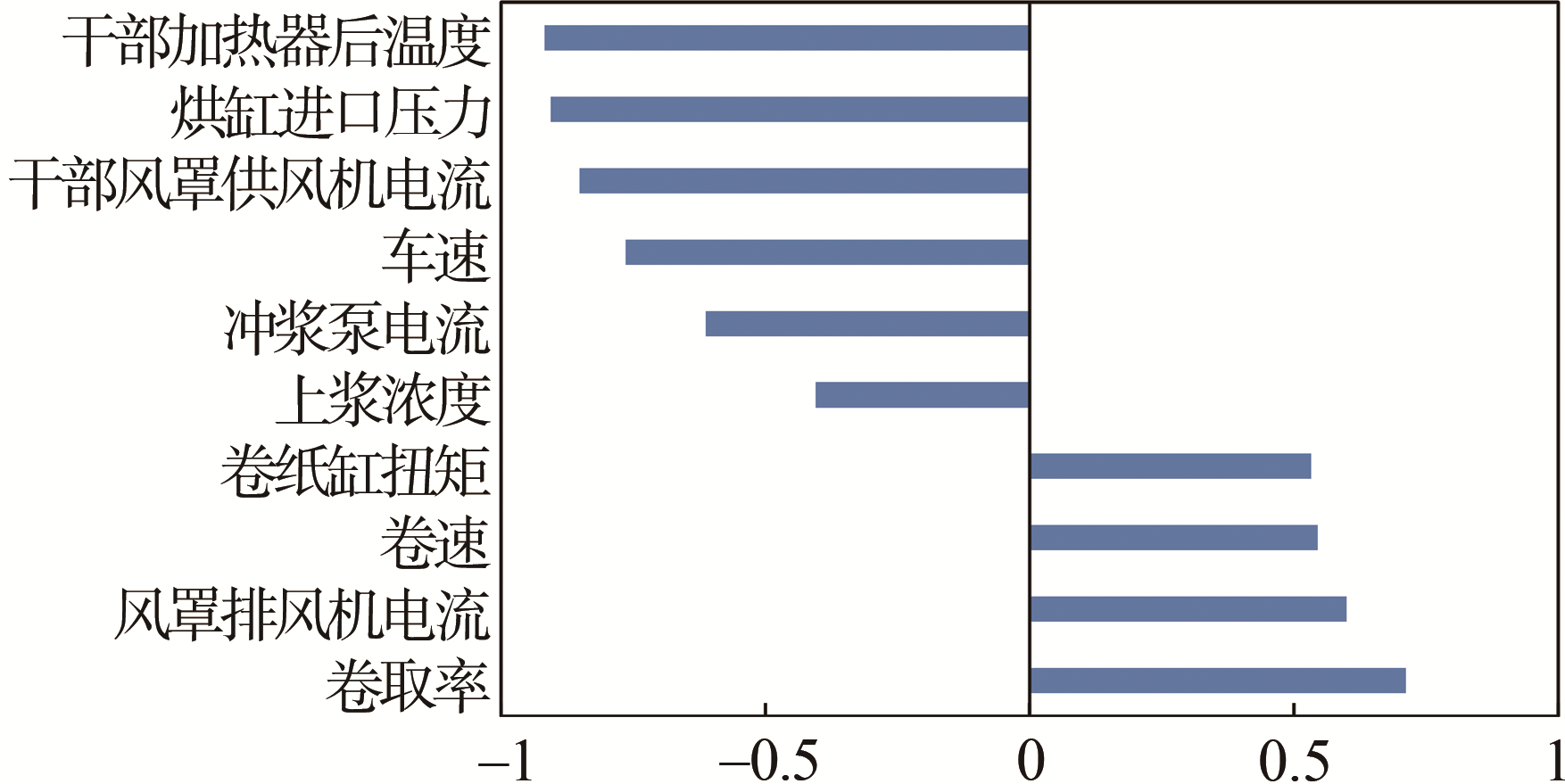
(c) 松厚度
图2 纸张各指标相特征选择结果
针对特征选择后的580组数据,划分80%训练数据集和20%测试集,训练集用来训练模型参数,测试集用来测试所训练的模型精度。基于GBDT算法,分别建立纸张抗张强度软测量模型、柔软度软测量模型和松厚度软测量模型,抗张强度软测量模型输入包含7种磨后浆料纤维形态(纤维平均长度、纤维平均宽度、扭结纤维百分比、断尾纤维百分比、纤维平均粗度、细小纤维含量(按长度)和分丝帚化率)及上述特征分析所选的
对于模型参数,GBDT算法主要有损失函数、每棵树深度、弱回归树棵树和学习率4个参数需要选择。损失函数常用的主要有最小二乘、最小绝对值差值、Huber损失和分位数损失,结合本研究数据波动较大,而Huber损失函数对异常值的抗干扰能力强,因此本研究选用Huber损失函数。然后确定每棵树深度,在数据量不大的情况下,树深度一般在3~6之间选取,树深度较高很容易导致模型过拟
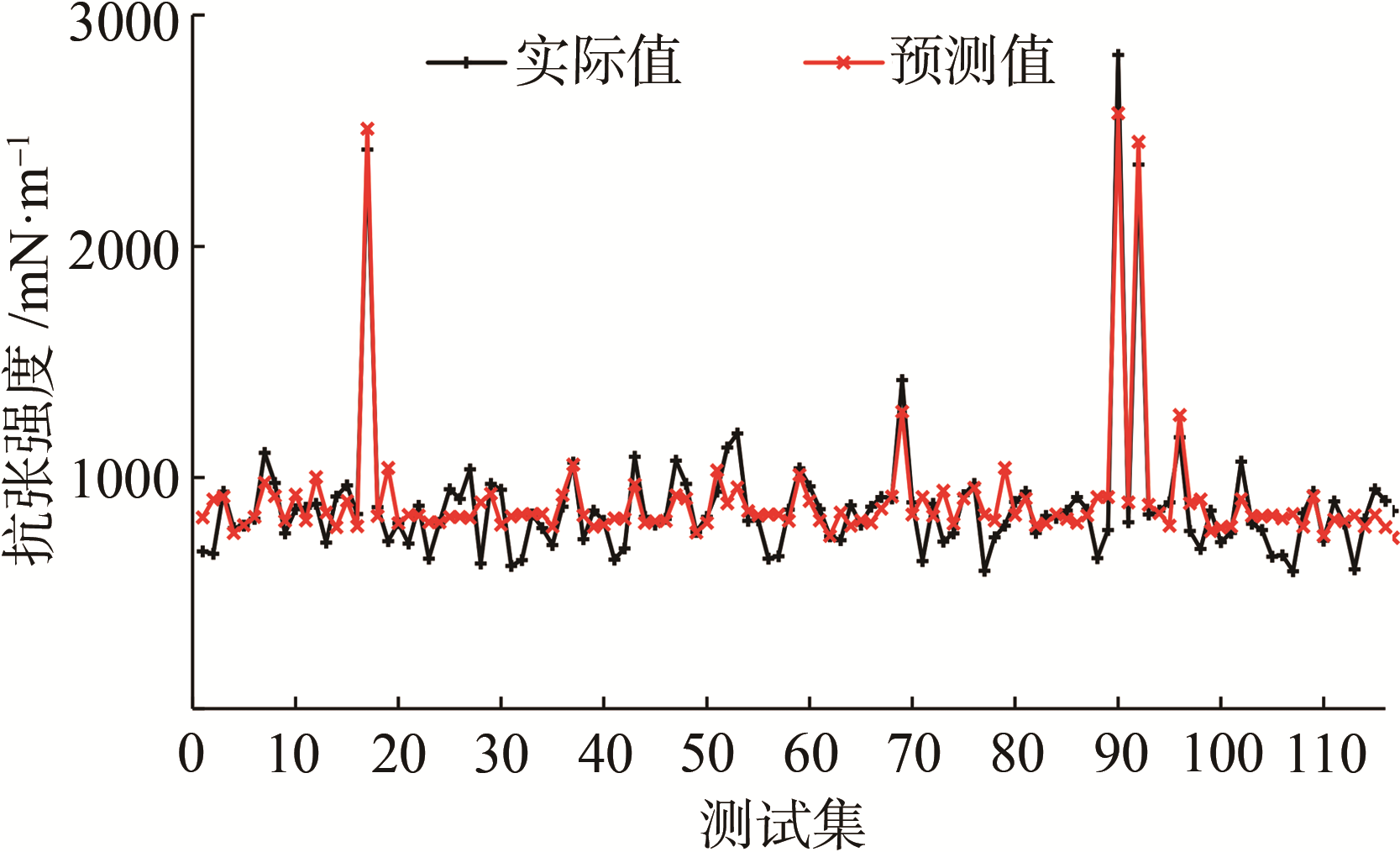
(a) 抗张强度
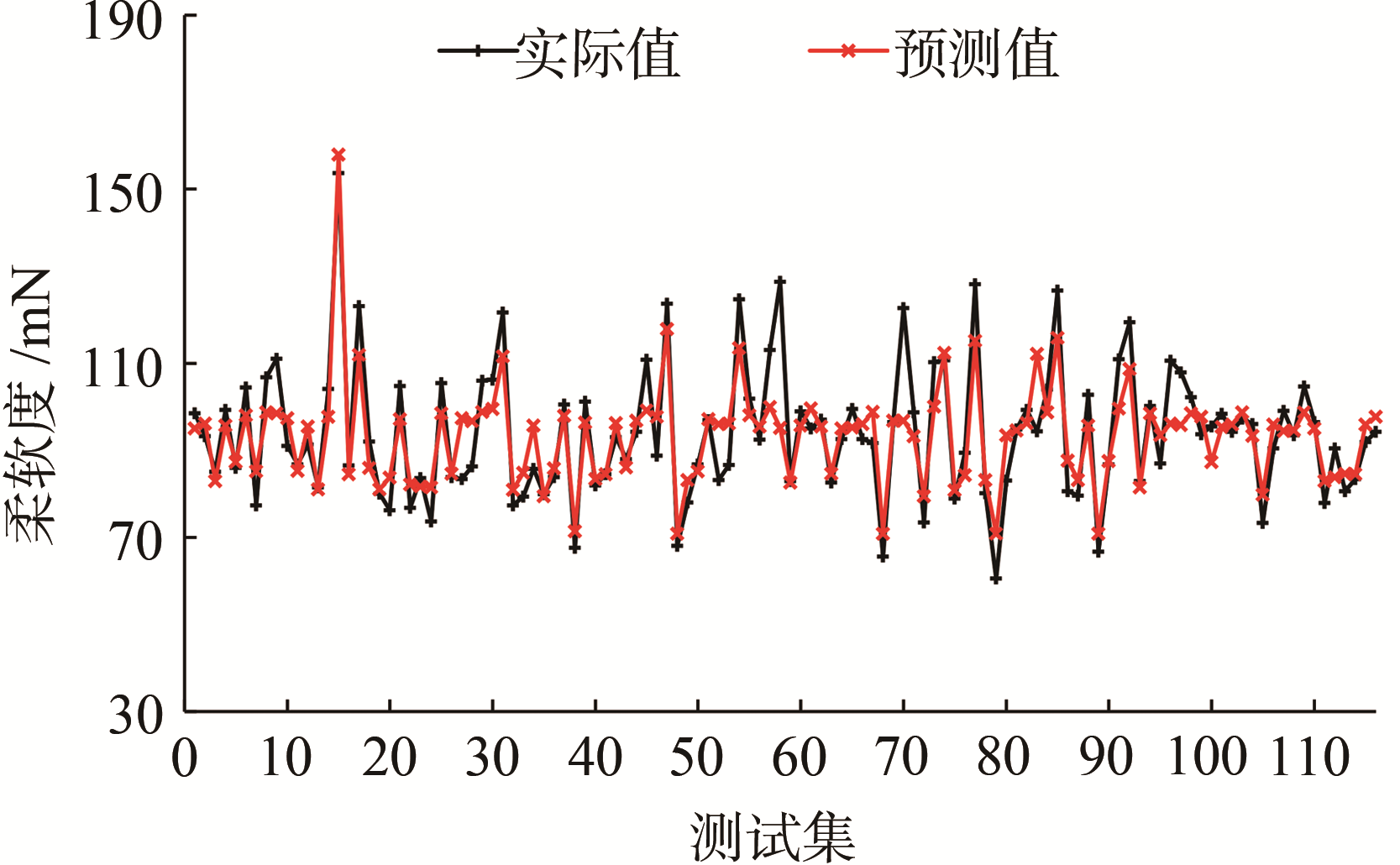
(b) 柔软度
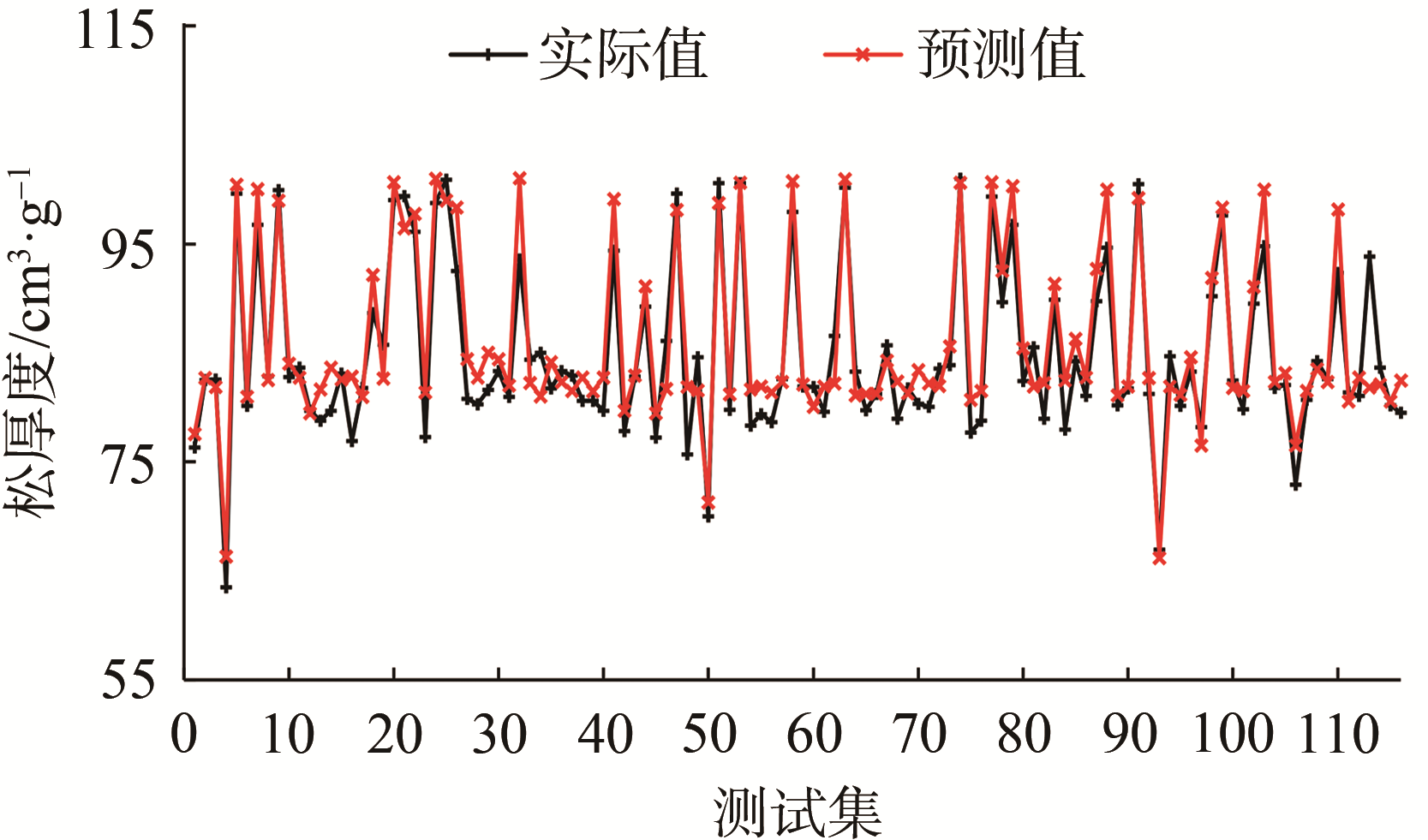
(c) 松厚度
图3 纸张各指标质量软测量模型测试结果
由
为验证模型的稳定性和泛化能力,本研究选用了现场的不同数据,来验证模型的有效性。所以再次从上述造纸企业MES上采集另一时间段内数据进行模型的验证,按照建模时数据的处理方式得到对应123组数据,输入到模型,输出为原纸的抗张强度、柔软度和松厚度指标,验证结果如
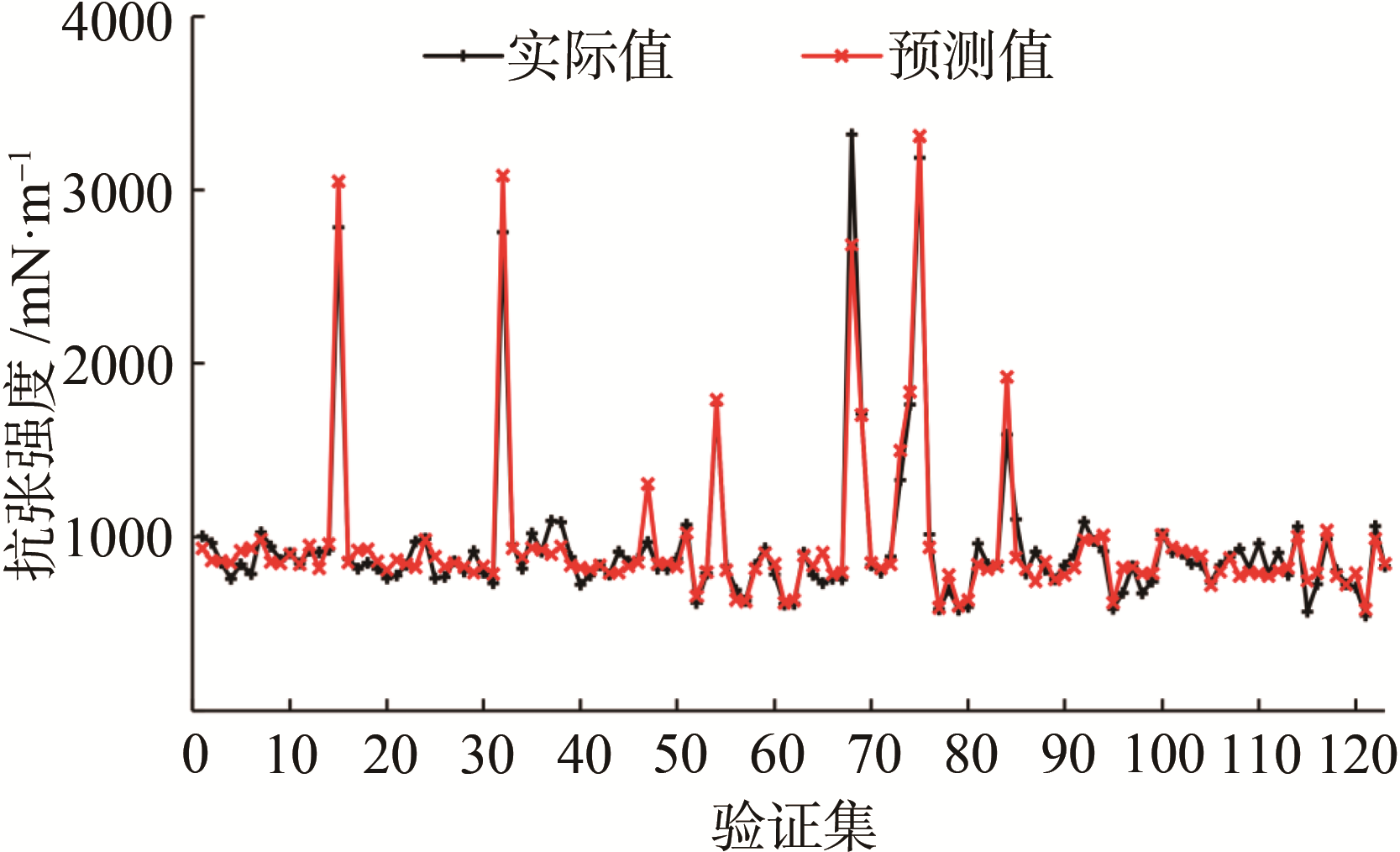
(a) 抗张强度
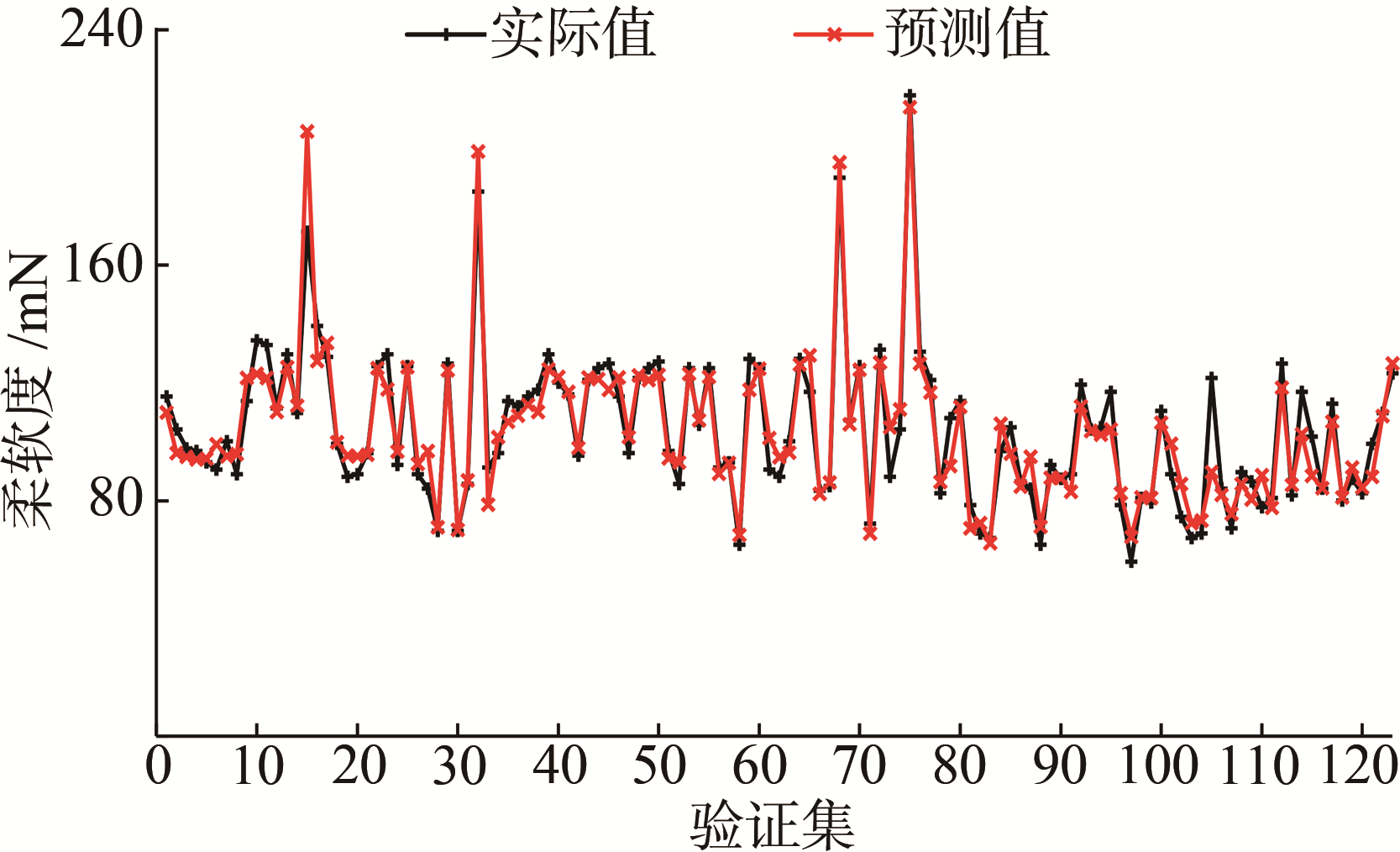
(b) 柔软度
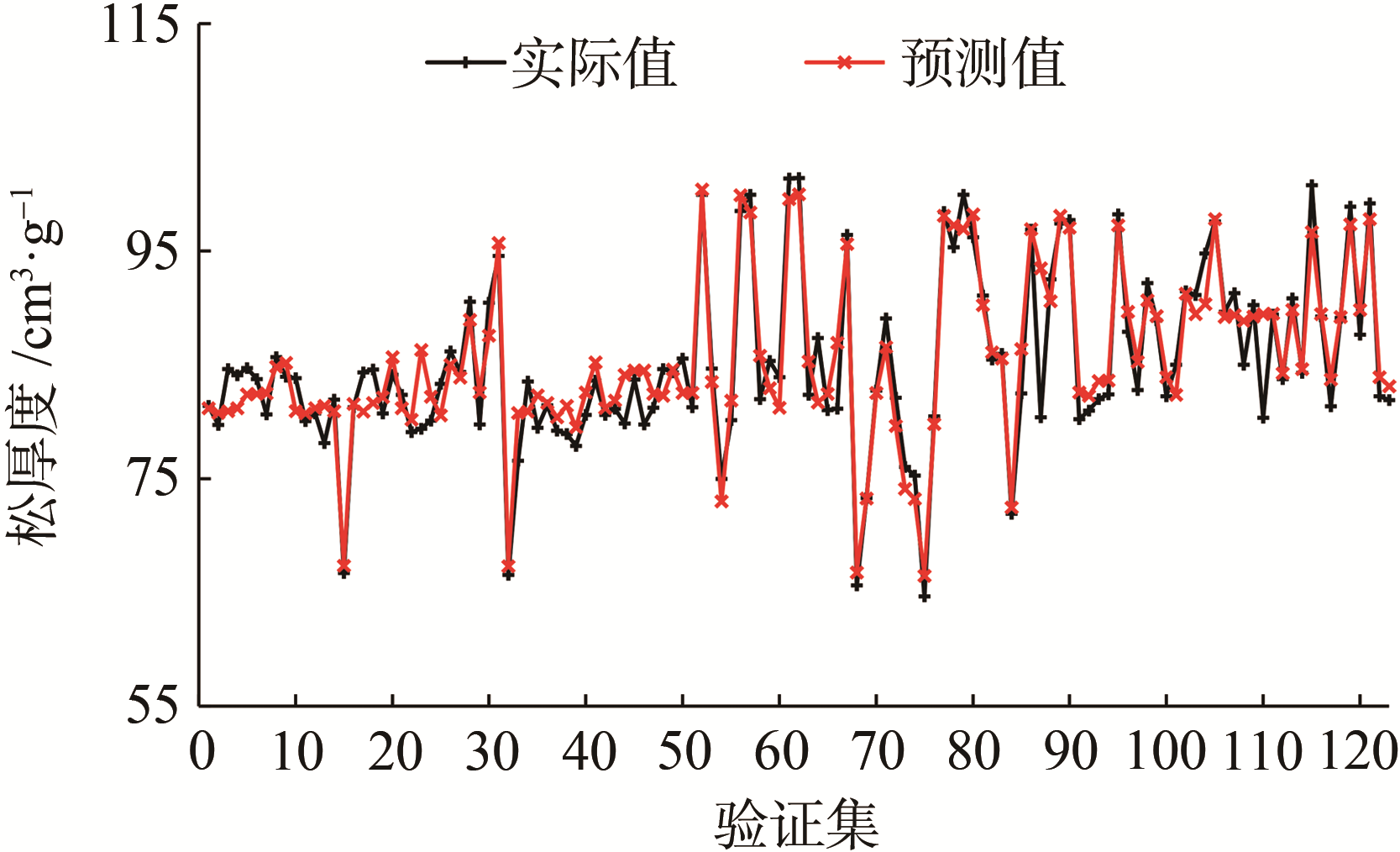
(c) 松厚度
图4 纸张各指标质量软测量模型验证结果
由
本研究针对造纸企业纸张关键物理指标进行软测量,基于机器学习的梯度增强决策树(GBDT)算法,采集造纸企业实时生产过程数据,建立造纸企业质量在线软测量模型及验证。结果发现,基于GBDT算法建立的质量在线软测量模型精度良好,满足质检误差需求。在采集新数据验证后,纸张抗张强度、柔软度、松厚度的平均相对误差分别为6.87%、6.88%和3.12%,表明模型精度泛化能力良好,且有较高的应用价值,可以为生产上监督异常、稳定产品质量及优化操作工艺提供价值依据。
参考文献
国务院关于印发《中国制造2025》的通知(摘要)[J]. 中国有色建设, 2015(2):5. [百度学术]
Notice of the State Council on Printing and Distributing "Made in China 2025"(Abstract) [J]. China Nonferrous Construction, 2015(2):5. [百度学术]
Pan Y, Chen S, Qiao F, et al. Estimation of real-driving emissions for buses fueled with liquefied natural gas based on gradient boosted regression trees[J]. Science of the Total Environment, 2019, 660: 741. [百度学术]
Man Y, Shen W, Chen X, et al. Modeling and simulation of the industrial sequencing batch reactor wastewater treatment process for cleaner production in pulp and paper mills[J]. Journal of Cleaner Production, 2017, 167: 643. [百度学术]
Man Y, Hong M, Li J, et al. Paper mills integrated gasification combined cycle process with high energy efficiency for cleaner production[J]. Journal of Cleaner Production, 2017,156:244. [百度学术]
Zhang X, Li J, Liu H, et al. Soft sensors for pulp freeness and outlet consistency estimation in the Alkaline Peroxide Machanical Pulping (APMP) high-consistency refining process[J]. Bioresources,2016,11(2):3598. [百度学术]
张美娟, 张素风, 万 婧. 浆液浓度对其制备PET沉析纤维形态及纸张性能的影响[J]. 中国造纸, 2016, 35(9):26. [百度学术]
ZHANG Meijuan, ZHANG Sufeng, WAN Jing. Effect of Slurry Concentration on the Morphology and Paper Properties of PET Precipitated Fibers [J]. China Pulp &Paper, 2016, 35 (9): 26. [百度学术]
彭金勇, 刘洪斌, 李甘霖, 等. 影响纸和纸板松厚度的主要因素[J]. 中国造纸, 2014, 33(6):64. [百度学术]
PENG Jinyong, LIU Hongbin, LI Ganlin, et al. Main Factors Affecting the Bulk of Paper and Paperboard [J]. China Pulp & Paper, 2014, 33 (6):64 [百度学术]
Trepanier R J. Pulp fiber quality and the relationship with paper tissue properties[C]//Tissue Conference and Expo 2017, The Power of TAPPI and RISI, 2017. [百度学术]
Samira G, Emad S. Effects of pulp refining on fiber properties——A review[J] Carbohydrate Polymers, 2015,115,785. [百度学术]
Zeng W, Zhang D, Fang Y, et al. Comparison of partial least square regression, support vector machine, and deep-learning techniques for estimating soil salinity from hyperspectral data[J]. Journal of Applied Remote Sensing,2018,12(2):1. [百度学术]
Kullander J, Nilsson L,Barbier C. Evaluation of furnishes for tissue manufacturing suction box dewatering and paper testing[J]. Nordic Pulp and Paper Research Journal, 2012, 27(1):143. [百度学术]
Man Y, Han Y, Wang Y, et al. Woods to goods: Water consumption analysis for papermaking industry in China[J]. Journal of Cleaner Production, 2018, 195: 1377. [百度学术]
Tsai H H. Global data mining: An empirical study of current trends, future forecasts and technology diffusions[J]. Expert Systems with Applications, 2012, 39(9):8172. [百度学术]
Natekin A, Knoll A. Gradient boosting machines, a tutorial[J]. Frontiers in Neurorobotics, 2013, 7: 21. [百度学术]
García Nieto P J, García-Gonzalo E, Arbat G, et al. Pressure drop modelling in sand filters in micro-irrigation using gradient boosted regression trees[J]. Biosystems Engineering,2018,171:41. [百度学术]
胡雨沙,李继庚,洪蒙纳. 基于PSO-LSSVM算法的造纸过程短期电力负荷预测模型[J].中国造纸学报,2019,34(1):50. [百度学术]
HU Yusha, LI Jigeng, HONG Mengna, et al. Short-term Power Load Forecasting Model of Papermaking Process Based on PSO-LSSVM Algorithm [J]. Transactions of China Pulp and Paper, 2019,34 (1): 50. [百度学术]
孟子薇. 基于数据驱动的生活用纸物理特性预测及其打浆工艺优化[D].广州:华南理工大学, 2019. [百度学术]
Meng Zi-wei. Data-driven Prediction of Tissue Paper Physical Properties and Optimization of Its Beating Process [D]. Guangzhou: South China University of Technology,2019. [百度学术]
孟子薇,洪蒙纳,李继庚.基于梯度增强回归树算法的磨浆过程打浆度软测量模型[J].造纸科学与技术,2019,38(1):83. [百度学术]
Meng Zi-wei, Hong Meng-na, Li Ji-geng. Soft Measurement Model of Beating Degree of Refining Process Based on Gradient Enhanced Regression Tree Algorithm [J] .Paper Science and Technology, 2019,38 (1): 83. [百度学术]
Thomas J,Mayr A, Bischl B, et al. Gradient boosting for distributional regression: faster tuning and improved variable selection via noncyclical updates[J]. Statistics and Computing, 2017, 28(6):1 [百度学术]