网刊加载中。。。

使用Chrome浏览器效果最佳，继续浏览，你可能不会看到最佳的展示效果，

确定继续浏览么?

复制成功，请在其他浏览器进行阅读

基于改进蚁群优化算法的中高速长网纸机速度链的控制

汤伟 ¹
马强 ¹
税宇阳 ²
王帅 ¹

1. 陕西科技大学电气与控制工程学院，陕西西安，710021； 2. 陕西科技大学机电工程学院，陕西西安，710021

中图分类号： TS736； TP273

最近更新：2019-11-22

DOI：10.11980/j.issn.0254-508X.2019.11.007

目录contents

摘要

对中高速长网纸机而言，确保速度链控制满足工艺要求对纸机正常运行有着重要意义。目前，纸机速度链控制多采用常规PID控制，但中高速长网纸机由于自身传动点多、车速快，故对闭环系统的响应速度和控制精度要求高，常规PID参数整定方法难以满足上述控制要求。蚁群优化算法（ACO）是一种适合多目标寻优的全局搜索算法，但传统蚁群算法易陷入局部最优及搜索较慢的问题，对此，本课题将信息素因子（α）和启发式因子（ $β$ ）按一定比例关系随迭代进行变化，提出一种改进蚁群优化算法，并将其应用于速度链PID控制器参数整定中。仿真结果表明，与常规PID控制相比，基于改进的蚁群优化算法PID控制系统响应速度更快、超调更小、抗干扰能力更好、鲁棒性更强。应用结果表明，该控制系统可保持纸机各部分速度长期稳定。

关键词

中高速长网纸机; 速度链控制; 改进蚁群优化算法; PID参数优化

速度链控制是纸机正常运行的基础，一旦传动点之间的速比失衡或者速度波动频繁，就会造成纸张的断裂或堆积，从而导致停机事故的发生^[

1,2,3]。造成传动点速比失衡的原因较多：在卷取部，电机拖动的负载随时间的变化发生改变从而导致传动点速度变化，如果不能快速准确地调整，则会导致速比失衡，若电机供电电压出现波动，也会导致速比失衡；纸机车速调整时，如果某一部分速度响应不及时，则会造成断纸^{[参考文献 4
Google Scholar 百度学术}4]。因此，对于传动系统速度链的控制十分重要。目前，速度链的控制一般采用PID控制，PID的参数整定大多采用试凑法和人工经验进行整定^{[参考文献 5
Google Scholar 百度学术}5]。但对于中高速长网纸机，由于车速快、传动点多、传统的参数整定法得到的参数难以满足高速运行情况下速度链控制系统对响应速度和精度要求。

蚁群优化算法（ACO）^[

6]是一种通过模拟自然界中蚂蚁寻找觅食最优路径而提出的仿生智能算法，具有正向反馈机制、鲁棒性强等特点，目前多应用于解决旅行商问题，通过在较优路径上增加信息素浓来增大下次寻优过程中被选择的概率。而评判路径优劣的准则由目标函数决定。利用蚁群算法的这些特点，将其应用于PID参数优化之中，通过对信息素浓度增减的判定标准进行修改，将目标函数改为与闭环控制系统超调量σ、上升时间t _r和调整时间t _s有关的函数，以此来判断闭环控制系统性能并作为信息素浓度增减的标准。对于性能较优的路径增加信息素浓度，可以提高被选择的概率。

本文在简要阐述速度链控制基本原理的基础上，将课题组改进的ACO用于PID控制器参数的改进，并将所得PID控制器用于造纸机传动速度链的控制。以仿真及应用结果证明论文算法的有效性。

1 速度链控制原理

纸机传动系统如图1所示，一般包括成形部、压榨部、干燥部、压光和卷取等几部分^[

7]。其中每部分都包含了一个到几个不等的导辊，其中一些导辊与电机相连，称为传动系统的传动点。剩下的导辊则是在传动点的驱动下，由网布或毛布拖动运行^{[参考文献 8
Google Scholar 百度学术}8]。

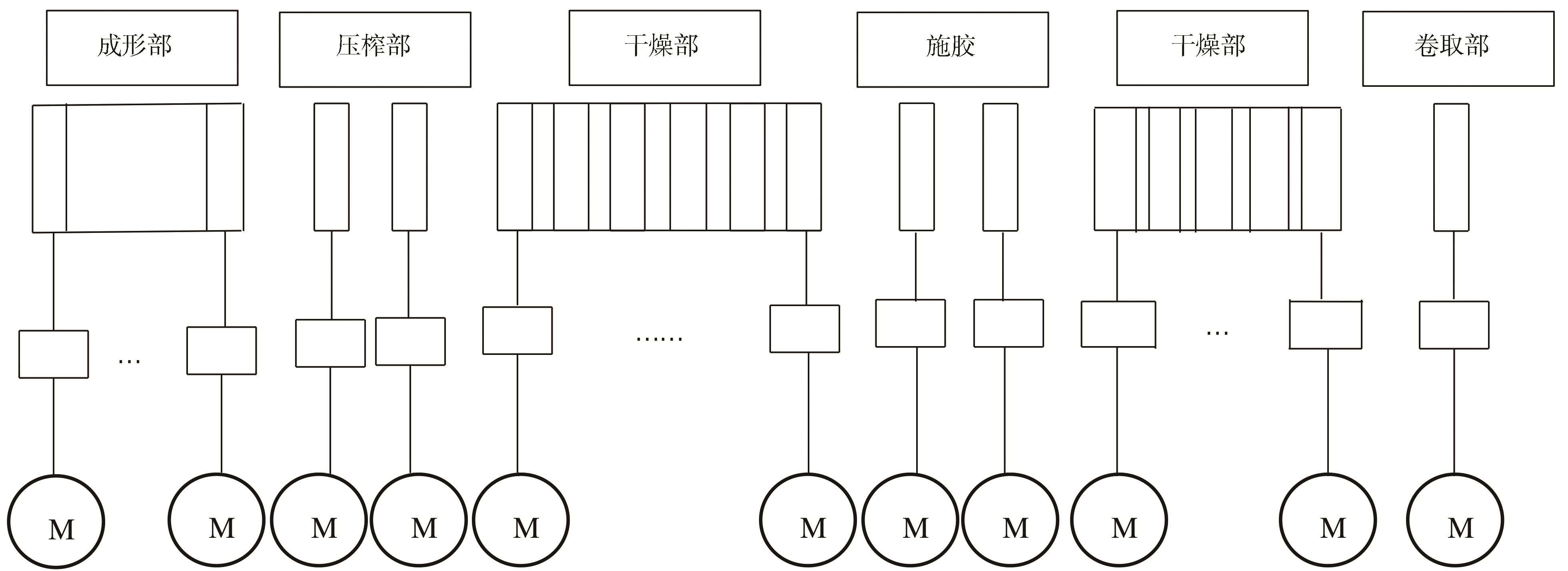
图1 速度链控制系统简图

所有的传动点共同组成一个链式结构，称为速度链。在纸张的生产过程中，由于工艺原因会造成纸张的延展伸长。因此，对于传动系统各个部分的速度要求也有所不同，所以必须对各传动点电机进行速度控制，保证各传动点速度稳定，相邻传动点之间速比稳定^[

9]。

2 ACO的改进

2.1　ACO的基本思想

蚂蚁在寻找食物时会在经过的路径上释放一种叫信息素的物质，在距离食物较短的路径上，信息素挥发的慢，残留浓度高，会吸引更多蚂蚁，最终所有的蚂蚁都会选择同一条路径，即为蚁群优化算法（ACO）^[

10]。

2.2　ACO数学模型

假设给定n个城市，从某一城市出发访问其余各城市1次后，再回到原出发城市，要求寻找出一条最短线路。在初始时刻，假设寻优过程的每条路径上的信息素浓度都相同。定义 $φ_{i j}$ （0）=C（C是一个常数），蚂蚁k（k=1.2.3…m）在寻优过程中，根据各条路径上信息素浓度的大小以一定的概率 $p_{i j}^{k}$ （t）决定转移的方向， $p_{i j}^{k}$ （t）可表示为式（1）。

$p_{_{i} j}^{^{k}} = (t) \{\begin{array}{l} \frac{[φ_{i j} {(t)]}^{α} [η_{i j} {(t)]}^{β}}{\sum_{s \in a l l o w e d_{k}} [φ_{i j} {(t)]}^{α} [η_{i j} {(t)]}^{β}} j \notin t a b u_{k} \\ 0 o t h e r w i s e \end{array}$

（1）

式中， $η_{i j}$ 为路径（i，j）的能见度； $φ_{i j}$ （t）为t时刻路径ij上的信息素量；α为信息素的相对重要性（α $\geq 0$ ），称为启发因子； $β$ 为能见度的相对重要性（ $β \geq 0$ ），称为期望启发因子。

蚁群中的m只蚂蚁全都完成一次旅行后，对城市间信息素含量的更新见式（2）和式（3）。

$φ_{i j} (t + 1) = ρ φ_{i j} (t) + Δ φ_{i j}$

（2）

$Δ φ_{i j} = \overset{m}{\sum_{k = 1}} Δ φ_{i j}^{k}$

（3）

式中， $Δ φ_{i j}^{k}$ 为蚂蚁k在本次循环中留在路径ij上的信息素量； $ρ$ 为信息素的持久因子，（ $0 \leq ρ < 1$ ）。

通常用ant-cycle system作为基本的讨论模型，该模型能够体现全局范围内最短的路径，同时也能够提高系统的收敛速度。其表达式见式（4）^[

11]。

$Δ φ_{i j}^{k} \{\begin{array}{l} Q / L_{K} 若蚂蚁 k 在本次循环中经过路径 i j \\ 0 否则 \end{array}$

（4）

式中，Q为常数； $L_{K}$ 为寻优路径的总长度。

2.3　ACO的改进及仿真

蚁群算法是求解组合最优问题的常用方法，具有较好的寻优效果。但该算法本身也存在一些缺陷，如寻优过程花费时间较长、容易出现停滞现象、陷入局部寻优等^[

12]。导致这些问题的主要原因是α、

$β$ 的选取不当。本文通过多次仿真实验发现在迭代过程中改变α、

$β$ 的比例关系会取得很好的实验结果。迭代初期，将α值设定的较小，

$β$ 值设定的相对较大，以启发式作为蚂蚁状态转移概率的一个主要参考因素，蚂蚁选择道路的概率大小主要由启发式决定，从而避免了信息素浓度的积累导致的局部寻优；随着迭代的进行，将α值变大，同时减小β值，增加信息素浓度在概率选择上的重要程度，会使信息素浓度高的路径上的信息素浓度近一步积累，加速蚁群算法的收敛速度，得到最优路径。α、

$β$ 比例关系如式（5）所示。

$(α, β) \{\begin{array}{l} α = 1 β = 5 α N_{c} \leq \frac{N_{c m a x}}{2} \\ α = 5 β β = 1 N_{c} > \frac{N_{c m a x}}{2} \end{array}$

（5）

以31个城市的旅行商问题为例。蚁群在31个城市随机出发，游历一星期，求经过所有城市的最优路径。

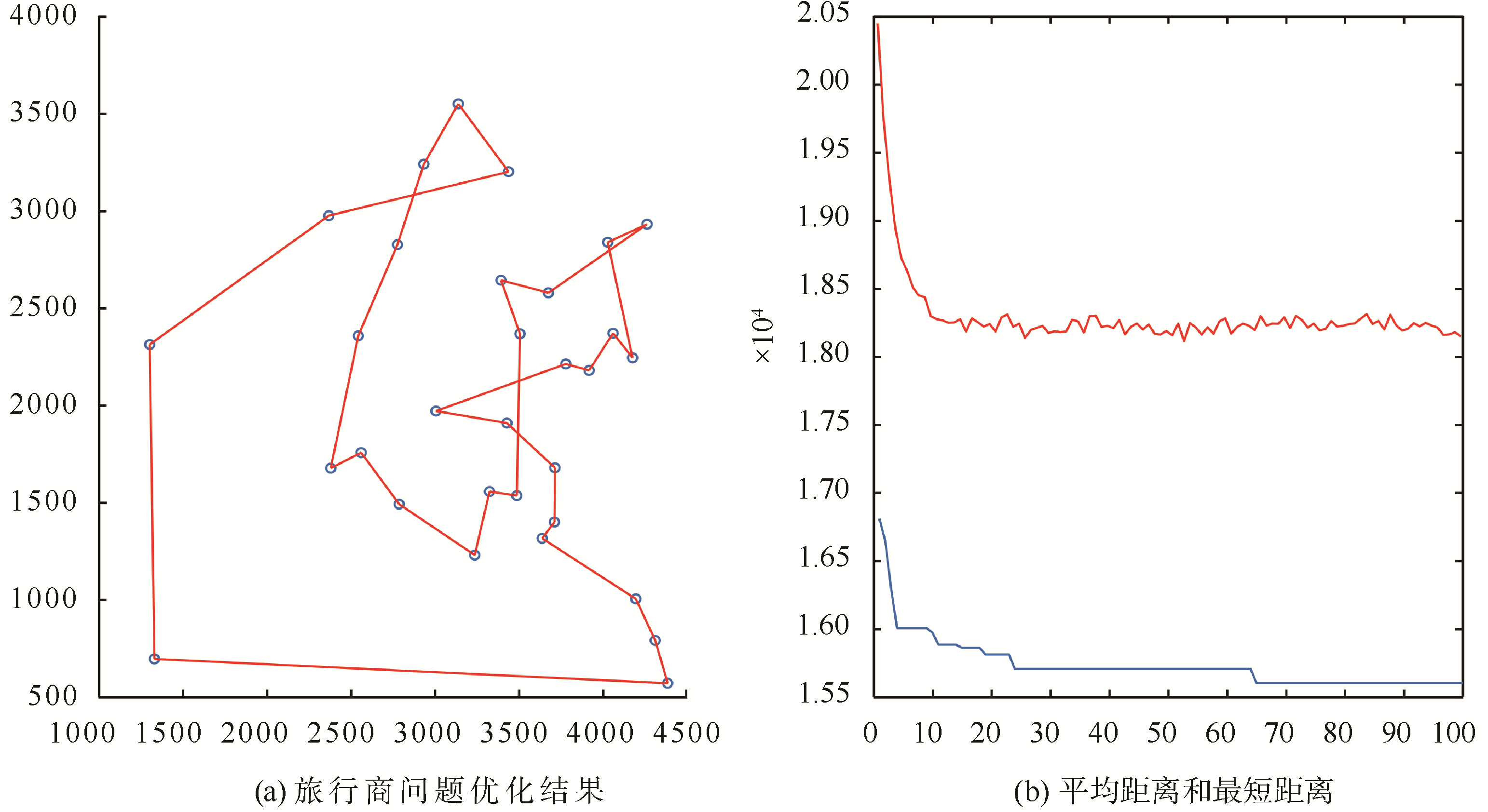
图2为传统蚁群算法旅行商问题仿真结果，整个过程经过65次迭代左右得到最优路径，其中，L _best=15601.9195329187。

图2 传统蚁群算法旅行商仿真图

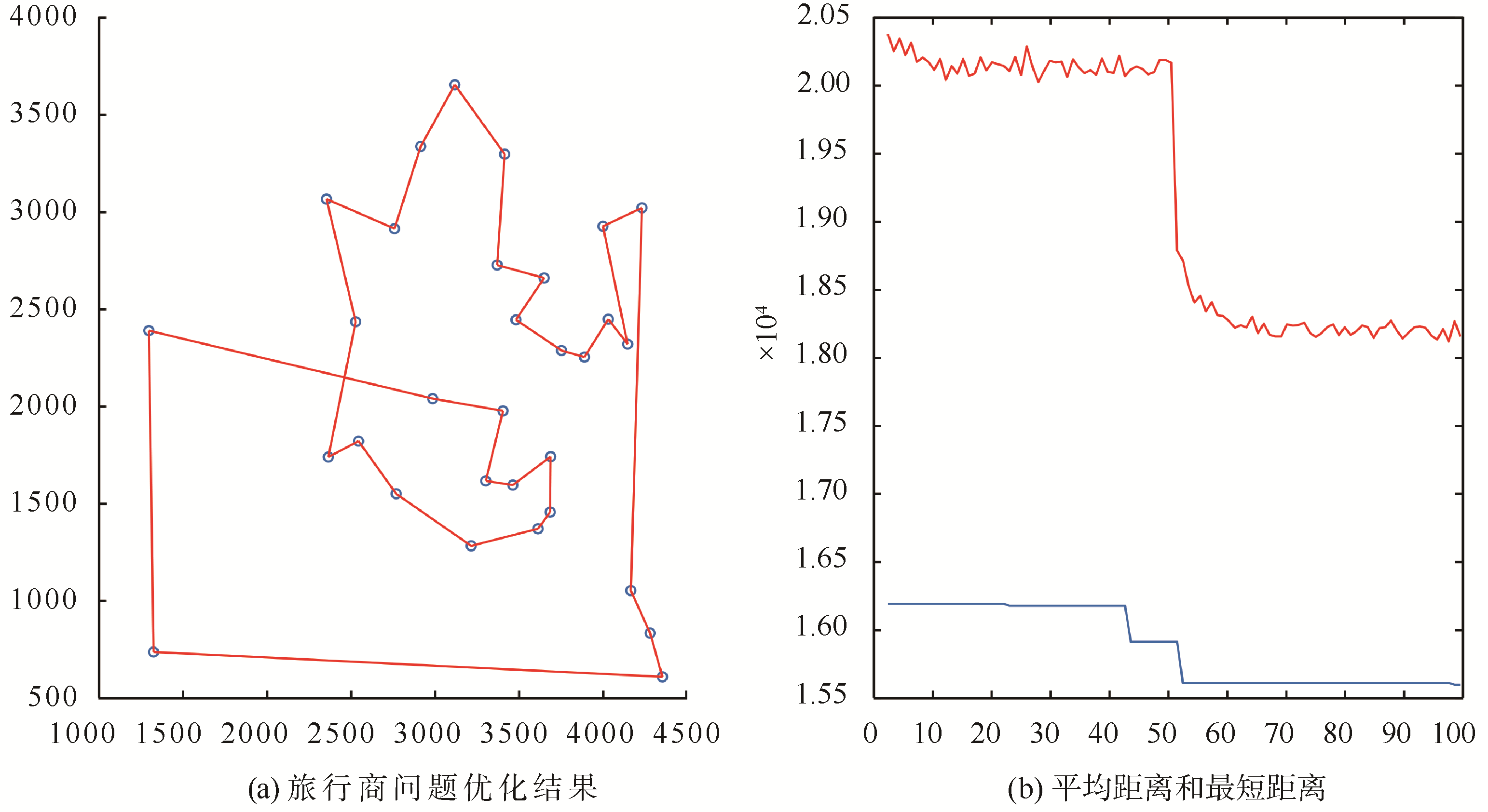
按上述优化过程对传统蚁群算法进行优化改进，经优化后的蚁群算法路径寻优如图3所示。虽然前期收敛速度缓慢，但是中期加速收敛并经过52次收敛得到最优解，最优路径L _best=15588.2935578277。

图3 改进ACO的旅行商仿真图

仿真实验表明，经过对蚁群算法的改进可以加快收敛速度，且经过改进的蚁群算法在寻优过程中最优路径比传统蚁群算法所得最优路径更短，结果更优。改进蚁群算法部分程序如图4所示。

图4 改进ACO的程序图

3 基于改进ACO的PID参数优化

3.1　基于改进ACO的PID控制系统结构

PID控制因为去结构简单、易于实现，目前被广泛的应用于工业控制，其控制系统原理图如图5所示。

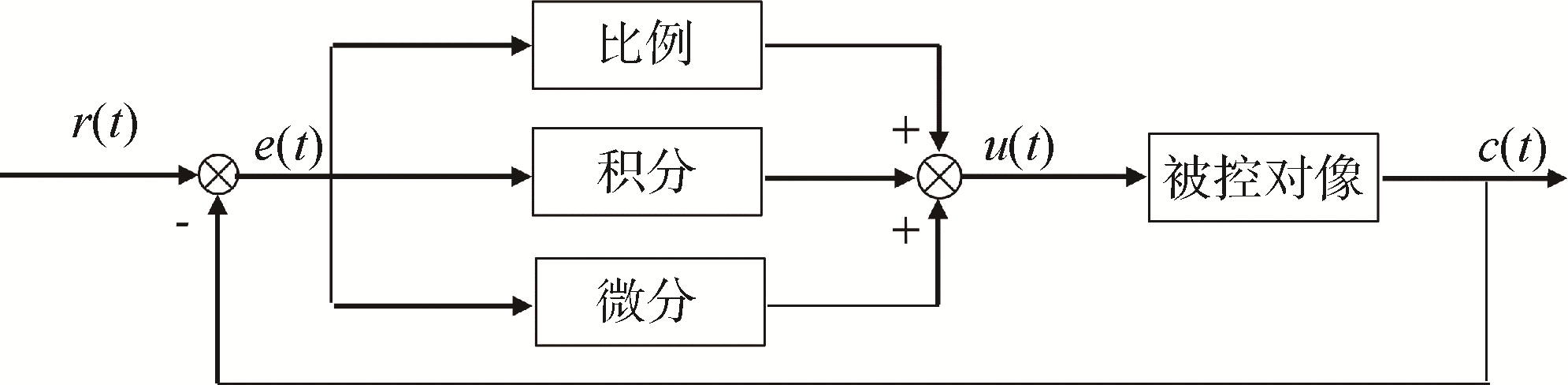
图5 PID控制原理图

当系统连续时，控制量与偏差量满足式（6）^[

13]。

$u (t) = K_{P} (e (t) + \frac{1}{T_{I}} \int_{o}^{t} e (t) d t + T_{D} \frac{d e (t)}{d t})$

（6）

当系统离散时，控制量和偏差量满足差分方程（7）和增量方程（8）。

$u (n) = K_{P} (e (n) + \frac{1}{T_{I}} \overset{n - 1}{\sum_{K = 0}} e (k) T + T_{D} \frac{e (n - 1) + e (n - 1)}{T})$

（7）

$Δ u (n) = K_{P} (e (n) - e (n - 1) + \frac{T}{T_{I}} e (n) + \frac{T_{D}}{T} [e (n) - 2 e (n - 1) + e (n - 2)])$

（8）

式中，u（n）为第n次控制量，e（n）为第n次误差， $K_{P}$ 为比例系数， $T_{I}$ 、 $T_{D}$ 分别为积分时间常数和微分时间常数。且 $K_{I}$ = $K_{P}$ / $T_{I}$ ， $K_{D}$ = $K_{P}$ · $T_{D}$ ，一般来说一组 $K_{P}$ $K_{I}$ $K_{D}$ ，可以决定控制系统性能的好坏。基于改进ACO的PID控制系统图如图6所示。

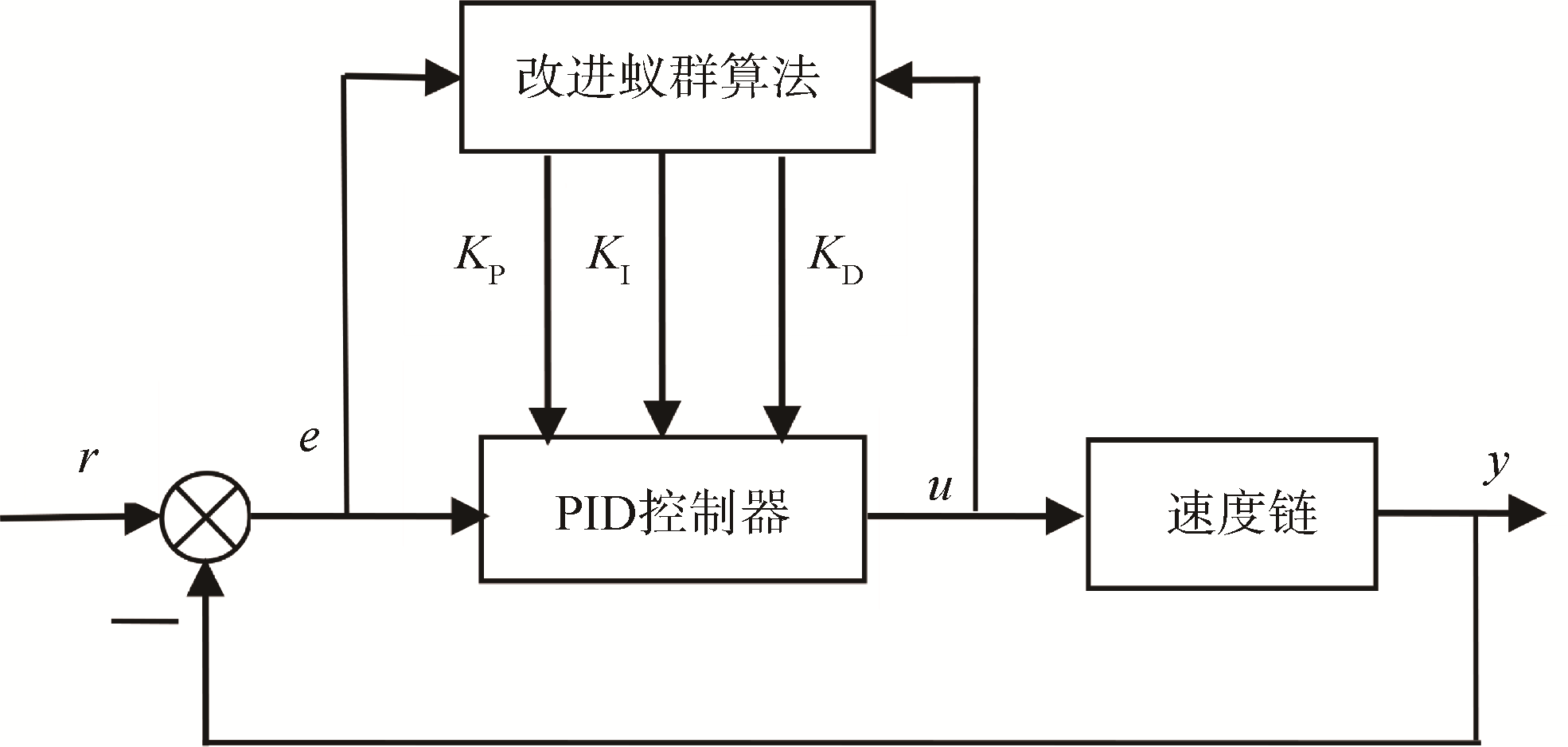
图6 改进ACO的PID控制系统

3.2　蚁群游历节点及路径的生成^{[参考文献 14
Google Scholar 百度学术}14]

利用改进ACO对PID参数优化过程：在XOY平面生成蚁群寻优路径，同时定义每条路径对应的PID参数。假设3个优化参数都有5位有效数字，小数点前面1位，后面4位。因此在设计XOY平面的过程中，每个单位横坐标代表1位有效数字，横坐标一共有3×5=15位，每个有效数字的取值范围在0~9之间也就是10位。所以XOY平面设计横坐标有15个单位长度，纵坐标为10个单位长度如图7所示。

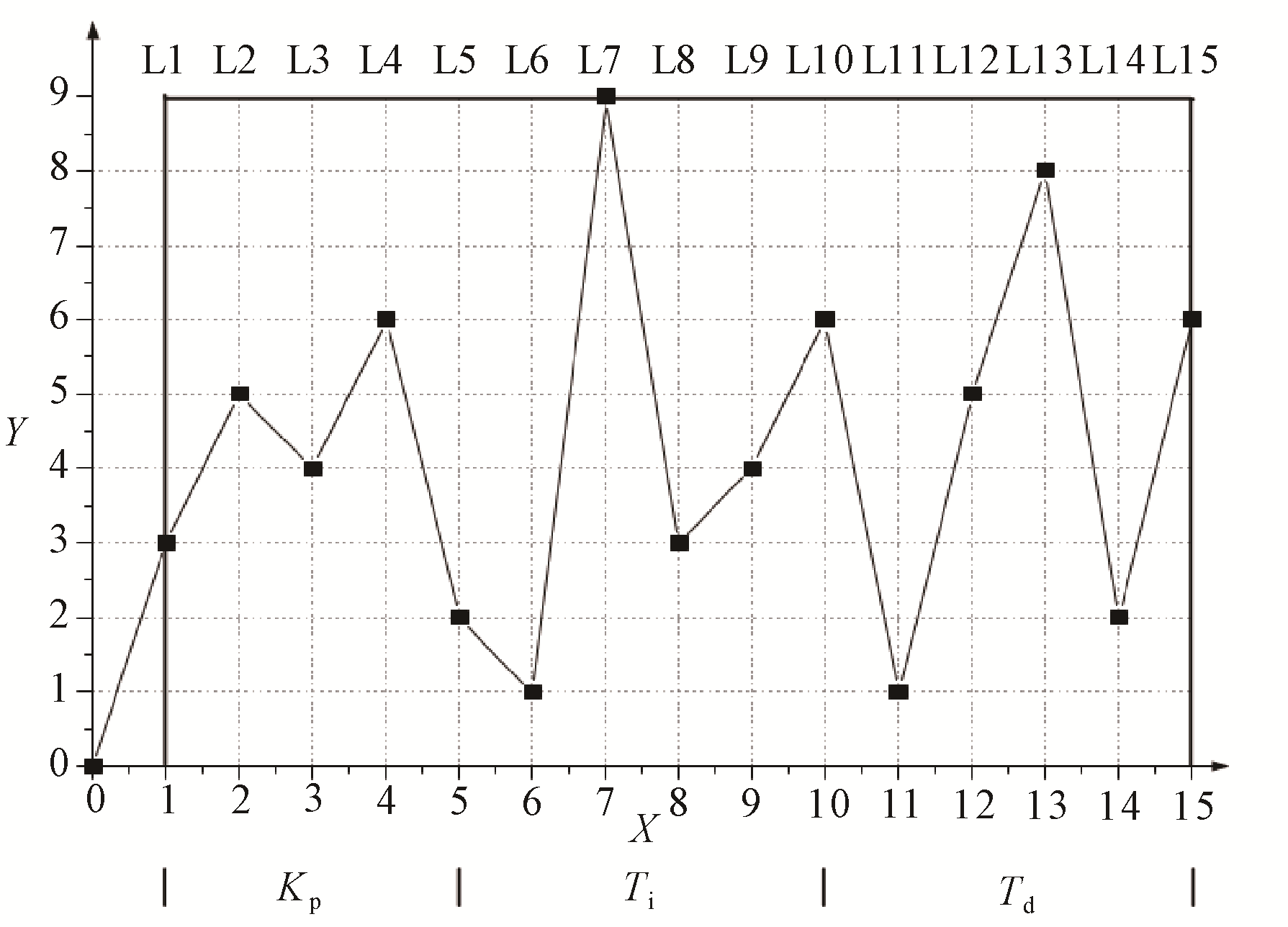
图7 路径生成示意图

图7代表蚂蚁随机选择的一条路径，蚂蚁从原点出发，经过每个横坐标时随机经过该横坐标与纵坐标相交节点 $(X_{i}, Y_{x i})$ （i=0，1，2…15），直到最后到达 $X_{15}$ ，在此过程中一共经过了15个节点。蚂蚁每在XOY平面游历一次，都会有一条包含15个坐标的折线，坐标对应PID参数如式（9）所示。

$\{\begin{array}{l} \begin{array}{l} K_{P} = Y_{X 1} \times 10^{0} + Y_{X 2} \times 10^{- 1} + Y_{X 3} \times 10^{- 2} + \\ Y_{X 4} \times 10^{- 3} + Y_{X 5} \times 10^{- 4} \end{array} \\ \begin{array}{l} K_{I} = Y_{X 6} \times 10^{0} + Y_{X 7} \times 10^{- 1} + Y_{X 8} \times 10^{- 2} + \\ Y_{X 9} \times 10^{- 3} + Y_{X 10} \times 10^{- 4} \end{array} \\ \begin{array}{l} K_{D} = Y_{X 11} \times 10^{0} + Y_{X 12} \times 10^{- 1} + Y_{X 13} \times 10^{- 2} + \\ Y_{X 14} \times 10^{- 3} + Y_{X 15} \times 10^{- 4} \end{array} \end{array}$

（9）

同时，由于搜索范围较大、耗时较长，可以首先使用Z-N法确定一组PID参数，并按式（10）确定蚁群算法搜索范围，这样可以大大节省搜索时间，提高搜索效率。

$\{\begin{array}{l} (1 - ε) K_{P}^{Z - N} \leq K_{P} \leq (1 + ε) K_{P}^{Z - N} \\ (1 - ε) K_{I}^{Z - N} \leq K_{I} \leq (1 + ε) K_{I}^{Z - N} \\ (1 - ε) K_{D}^{Z - N} \leq K_{D} \leq (1 + ε) K_{D}^{Z - N} \end{array}$

(10)

式中， $ε$ 取值范围为0~1。

3.3　蚁群游历节点及路径的选择

由于蚁群算法优化PID参数与传统的TSP问题有所区别，本文对旅行商问题中的状态转移概率等公式进行调整，使其满足解决PID参数优化问题需要。

其中，蚂蚁K在t时刻由 $X_{i - 1}$ 上某一节点 $Y_{i - 1, j}$ 向上 $X_{i}$ 某一节点 $Y_{i, j}$ 转移的概率计算见式（11）。

$P_{(X_{i}, Y_{i, j}, t)}^{K} = \{\begin{array}{l} \frac{φ {(X_{i}, Y_{i, j}, t)}^{α} η {(X_{i}, Y_{i, j}, t)}^{β}}{\overset{9}{\sum_{j = 0}} φ {(X_{i}, Y_{i, j}, t)}^{α} η {(X_{i}, Y_{i, j}, t)}^{β}} \\ 0 \end{array}$

（11）

式中， $φ$ 、 $η$ 所表示意义与式（1）有所差别，分别表示节点上的信息素浓度以及节点能见度。在此，对启发式重新定义为式（12）。

$η (X_{i}, Y_{i, j}, t) = \frac{10 - | Y_{i, j} - Y_{i, j}^{b e s t} |}{10}$

（12）

其中 $Y_{i, j}^{b e s t}$ 为当前最优路径对应的各节点纵坐标。同时，对于信息素的更新规则参考式（2）、式（3）、式（4），并对式（4）做出修改，将修改信息素由路径改为目标函数。

目标函数的作用是反映系统的动态性能以及稳态性能。在此，目标函数定义为式（13）。

$f = λ_{σ} (\frac{σ}{σ_{1}}) + λ_{t_{r}} (\frac{t_{r}}{t_{r_{1}}}) + λ_{t_{s}} (\frac{t_{s}}{t_{s_{1}}})$

（13）

式中， $σ_{1}$ 、 $t_{r_{1}}$ 、 $t_{s_{1}}$ 为Z-N法整定的PID参数对应的系统超调量、上升时间以及调节时间； $σ$ 、 $t_{r}$ 、 $t_{s}$ 为蚂蚁K经历的路径节点所生成的PID参数对应的控制系统动态性能。 $λ_{σ}$ 、 $λ_{t_{r}}$ 、 $λ_{t_{s}}$ 为权值，一般为经验所得。在此取 $λ_{σ}$ =0.6， $λ_{t_{r}}$ =0.2， $λ_{t_{s}}$ =0.2。

3.4　PID参数优化整定步骤^{[参考文献 15
Google Scholar 百度学术}15]

Step1：初始化。设置蚁群算法相关参数，如蚁群数量m，最大迭代次数NC_Max，信息素浓度、启发式和启发因子等。

Step2：利用Z-N法计算PID 3个参数，并按式（10）确定蚁群搜索范围。

Step3：将蚂蚁放置原点并开始爬行，其向各个节点爬行的概率按式（11）确定。

Step4：所有蚂蚁每完成一次从原点历经15个节点的爬行后，完成一次爬行过程，记录15个节点的节点坐标，按式（9）计算对应的PID参数。

Step5：将PID参数赋值给PID控制器，运行系统仿真，计算目标函数值，并将最优结果记录下来。

Step6：按照式（2）、式（3）、式（4）、式（11）、式（12）更新信息素浓度。

Step7：返回Step1进行下一次迭代，直到到达最大迭代次数停止。

4 仿真与实验结果

为验证改进ACO的效果，基于MATLAB软件进行仿真实验。纸机速度链系统可视为由变频器和三相异步电机组成。在仿真建模过程中^[

12]，可将异步电机近似看作输入为频率f、输出为转速n的单变量线性环节，其传递函数为

$A (s) = \frac{K}{T s + 1}$ ，

$K = \frac{n}{f}$ 。把变频器也看作一阶惯性环节，当变频器输入控制电压为u，输出为f时，其传递函数为

$B (s) = \frac{K_{1}}{T_{1} s + 1}$ ，其中

$K_{1} = \frac{f}{u}$ 。按照控制系统的基本参数可设定控制器的控制对象传递函数为式（14）^{[参考文献 16
Google Scholar 百度学术}16]。

$G (s) = \frac{20}{s^{2} + 3.6 s + 1}$

（14）

4.1　设定值跟踪性能比较

分别将改进ACO与传统ACO、Z-N法进行仿真实验对比，3种不同控制方法整定出的PID参数如表1所示，搭建的Simulink模型如图8所示。

表1 不同控制方法下参数整定

控制方法	K _P	K _I	K _D
Z-N	0.1958	0.0224	0.1425
ACO	0.1984	0.0226	0.1211
改进ACO	0.0932	0.0244	0.0236

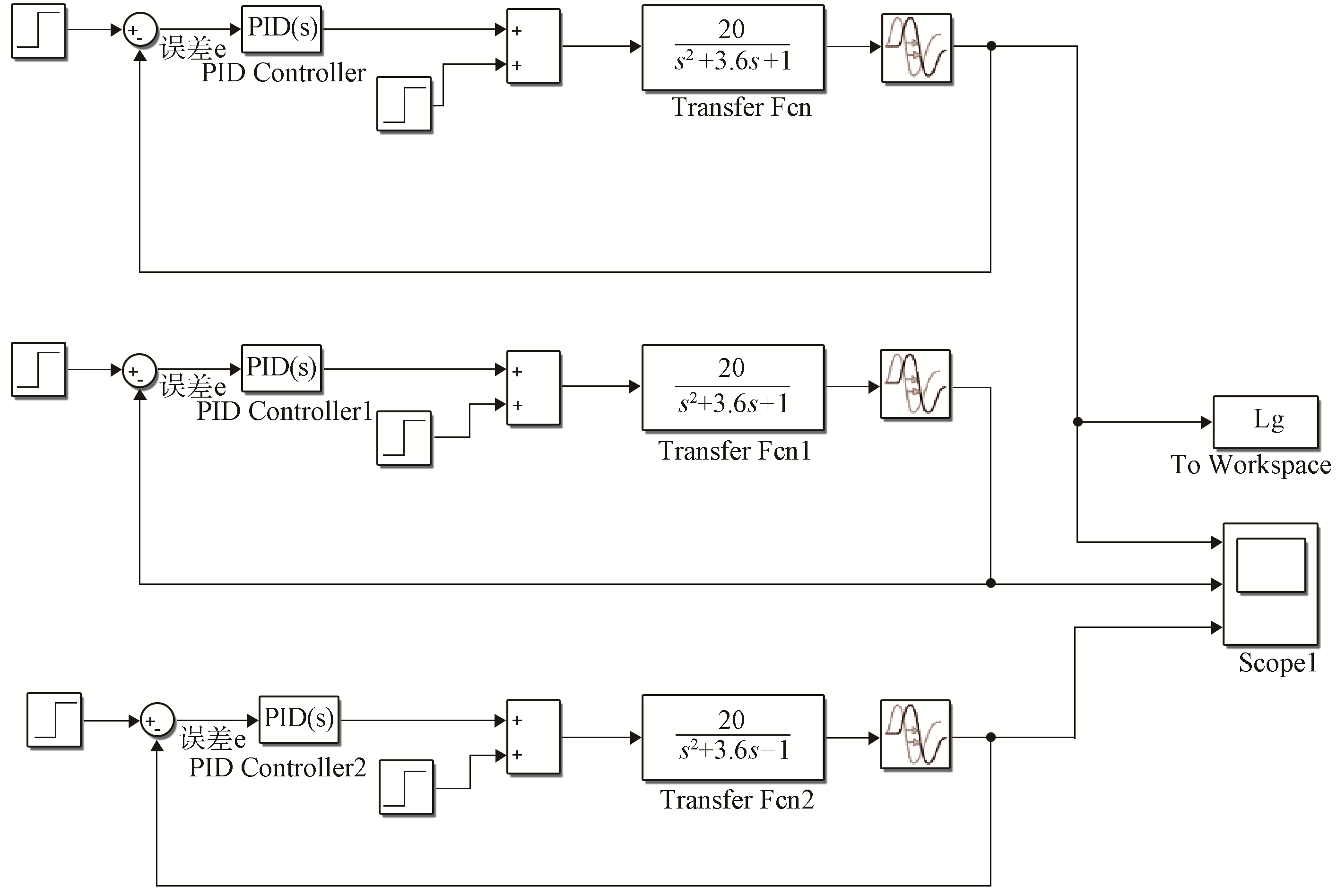
图8 不同控制方法下的Simulink模型搭建图

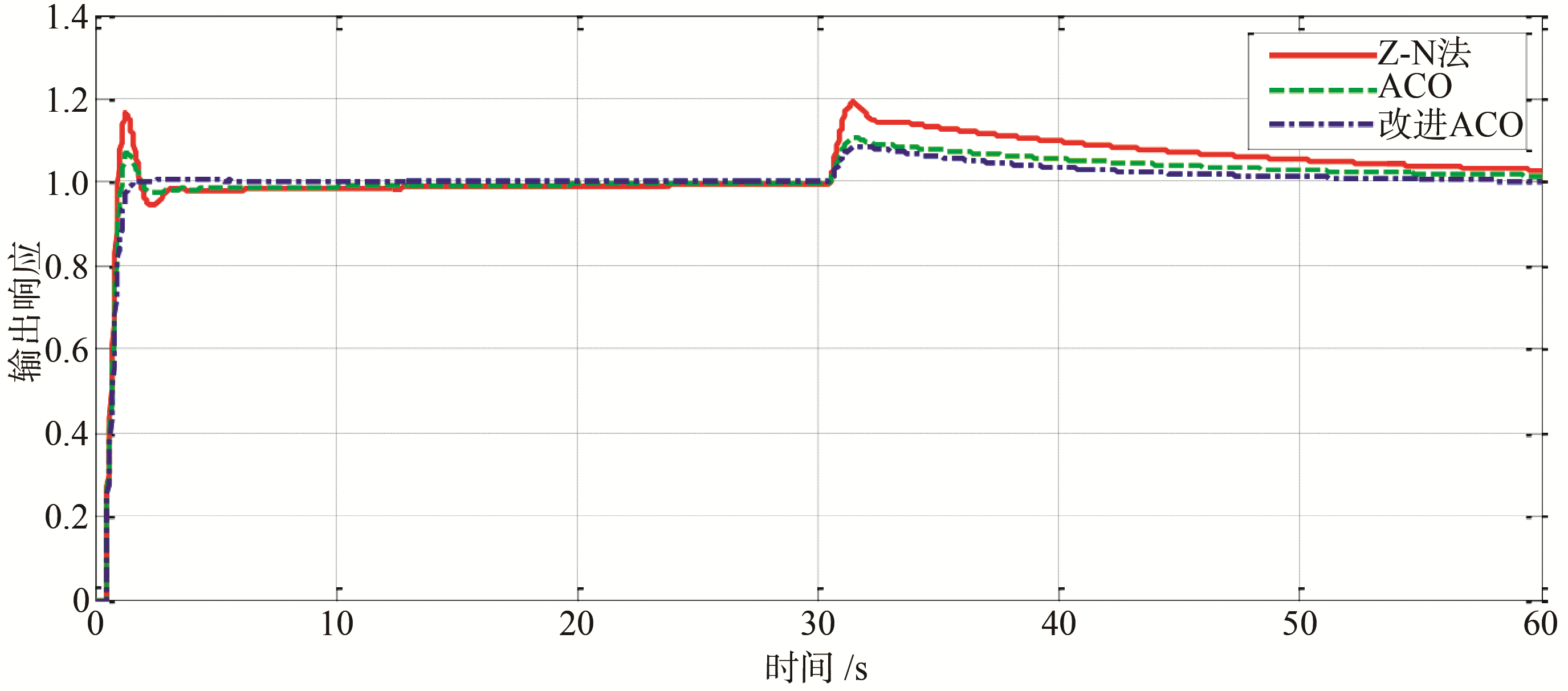
系统在3种控制方法下，分别加入单位阶跃信号，实际生产中，纸张定量及种类发生变化时均会对系统产生干扰，为验证系统的抗干扰性，在第30 s添加幅值为1的阶跃信号作为干扰信号，最终获得的系统阶跃响应曲线如图9所示，阶跃响应下的系统动态性能指标如表2所示，阶跃扰动下的系统动态性能指标如表3所示。

图9 阶跃响应及阶跃扰动下3种算法的系统响应曲线

表2 阶跃响应下3种算法的系统动态性能指标

控制方法	调整时间t/s	超调量σ/%
Z-N	8	18
ACO	5	9
改进ACO	3	3

表3 阶跃扰动下3种算法的系统动态性能指标

控制方法	波动时间t/s	超调量σ/%
Z-N	30	20
ACO	30	16
改进ACO	22	13

由表2可知，与Z-N法及ACO相比，改进ACO控制系统超调量最小，调整时间最小。由表3可知，在加入阶跃扰动的情况下，基于改进ACO令系统的超调量最小，波动时间最短，说明改进ACO的系统响应速度最快、调节时间最短、抗干扰性能最好。

4.2　鲁棒性能比较

实际生产中被控对象数学模型受非线性因素的影响而失配，失配20%后的数学模型仿真如图10所示。

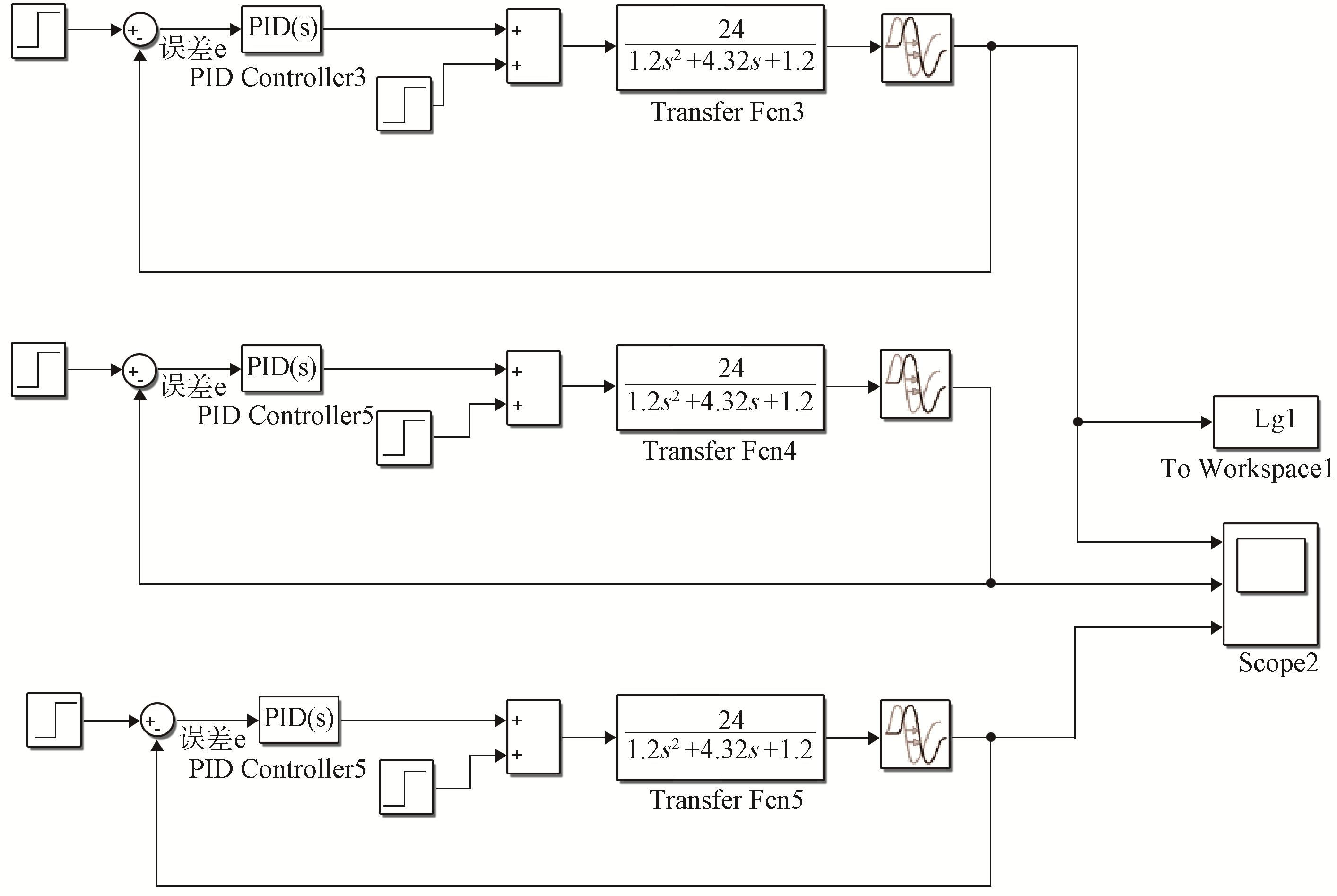
图10 失配20%后的数学模型仿真图

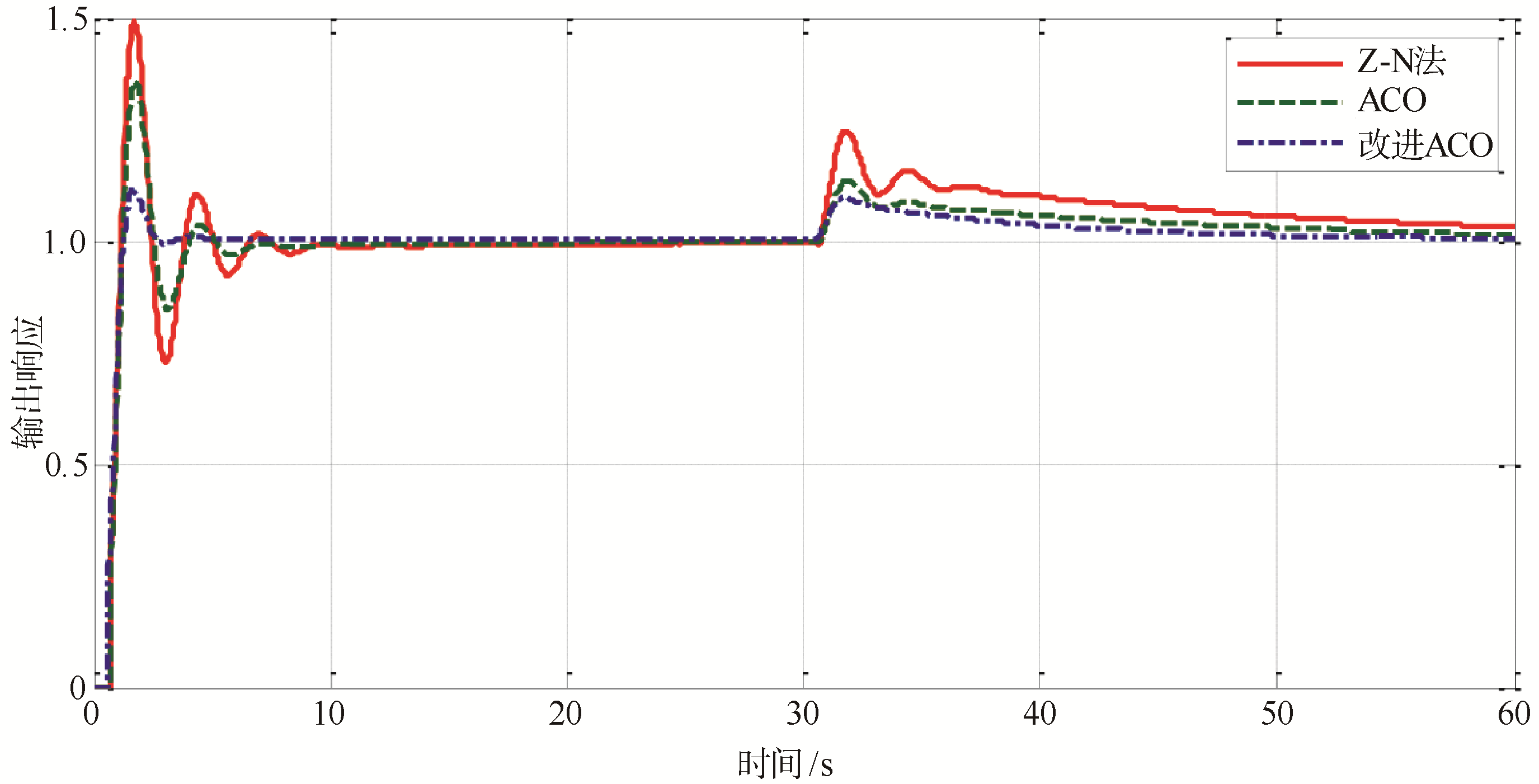
在被控对象模型失配的情况下，分别对3种控制方法加入阶跃信号，并在第30 s加入幅值为1的阶跃信号作为干扰信号，最终获得的模型失配下系统阶跃响应曲线如图11所示，阶跃响应下的系统动态性能指标如表4所示，阶跃扰动下的系统动态性能指标如表5所示。

图11 模型失配下阶跃响应及阶跃扰动下3种算法的系统响应曲线

表4 模型失配时阶跃响应下3种算法的系统动态性能指标

控制方法	调整时间t/s	超调量σ/%
Z-N	15	50
ACO	13	32
改进ACO	8	12

表5 模型失配时阶跃扰动下3种算法的系统动态性能指标

控制方法	波动时间t/s	超调量σ/%
Z-N	35	26
ACO	33	19
改进ACO	24	17

上述仿真结果表明，与Z-N法及传统ACO相比，基于改进的ACO PID控制系统在被控对象数学模型失配时在速度链闭环控制系统中的响应速度更快、超调量更小抗干扰能力更强。且经过改进ACO优化的PID参数鲁棒性更强。

5 算法实现及应用

目前，该算法已应用于保定某造纸厂传动控制系统。在实际设计中，选取S7-400PLC，变频器及三相交流电机与工业控制计算机组成纸机的三级传动控制系统，各级之间通过profibus-DP或光纤实现通信，同时使用OPC技术，实现在上位机中的MATLAB与WinCC进行数据交换。其中图12是长网纸机卷取部速度实时监控图，在卷取过程中，电机带动的导辊负载时刻发生变化，监控图显示，卷取部分速度平稳，波动幅度很小。纸机正常运行，无断纸停机情况发生。

图12 长网纸机卷取部速度实时监控图

6 结论

本文提出的基于改进蚁群算法（ACO）的PID控制既提高了蚁群算法的收敛速度，又解决了算法本身因为影响因子所导致的局部寻优问题，与传统ACO相比，改进后的ACO具有更好的寻优结果。同时，MATLAB仿真结果也表明，在速度链控制系统中，基于改进ACO的PID控制系统相较于传统ACO PID控制系统和常规PID控制系统的响应速度更快、超调量小、抗干扰能力更强且鲁棒性也更好。速度链控制系统运行结果表明，各传动点速度可以更好地跟踪设定值，速度波动幅度很小，车速升降各传动点速度响应快，各部分之间速比稳定。纸机可保持长时间不断纸、不停机，有效减少了企业因停机造成的损失。

参考文献

Feng Haichuan . Design of transmission control system for high speed paper machine[D]. Ji’nan:Shandong University，2007. [百度学术] [Google Scholar]

冯海川 . 高速纸机交流变频分部传动控制系统设计[D]. 济南：山东大学, 2007. [百度学术] [Google Scholar]

WANG Sue, HAO Pengfei . Present Situation and Development Trend of Paper Machine Transmission System[J]. China Pulp & Paper, 2007, 26(1):52.. [百度学术] [Google Scholar]

王素娥, 郝鹏飞 . 纸机传动系统的现状及发展趋势[J]. 中国造纸, 2007, 26(1):52.. [百度学术] [Google Scholar]

JIN Yongfan . Application of Master-slave Control in Paper Machine Drive System[J]. China Pulp & Paper, 2006, 25(1):67. [百度学术] [Google Scholar]

金勇范 . 主从控制在纸机传动系统中的应用[J]. 中国造纸, 2006, 25(1):67. [百度学术] [Google Scholar]

MA Wenming . Design and Application of Paper Machine Drive Control System Based on A-B Platform[J]. China Pulp & Paper, 2017, 36(4):55. [百度学术] [Google Scholar]

马文明 . 基于A-B平台的造纸机传动控制系统设计及应用[J]. 中国造纸, 2017, 36(4):55. [百度学术] [Google Scholar]

Zhong Liang . Design of Electric Drive Control System of Paper Machine Based on PLC[D].Beijing : North China Electric Power University ,2014. [百度学术] [Google Scholar]

钟　亮 . 基于PLC的纸机电气传动控制系统设计[D]. 北京：华北电力大学, 2014. [百度学术] [Google Scholar]

Pin Z , Xiao-Ping L , Hong-Fang Z . An ant colony algorithm for job shop scheduling problem[C]// Intelligent Control and Automation, 2004. [百度学术] [Google Scholar]

XU Deyu . Paper Machine Frequency Conversion Drive PLC Control[J]. China Pulp & Paper, 2005, 24(10):48. [百度学术] [Google Scholar]

许德玉 . 纸机变频传动的PLC控制[J]. 中国造纸, 2005, 24(10):48. [百度学术] [Google Scholar]

Chen Xi .Research on Section-drive Multi-motor Synchronous Control System of Paper Machine[D].Ji’nan:Shandong University, 2009. [百度学术] [Google Scholar]

陈　曦 . 造纸机分部传动多电机同步控制系统研究[D]. 济南：山东大学, 2009. [百度学术] [Google Scholar]

MENG Yanjing, LI Honglei . Research on Transmission Control System of High-speed Sanitary Paper Machine[J]. China Pulp & Paper, 2011,30(6):53. [百度学术] [Google Scholar]

孟彦京, 李红垒 . 高速卫生纸机传动控制系统研究[J]. 中国造纸, 2011, 30(6):53. [百度学术] [Google Scholar]

Duan Haibin . Principle and application of ant colony algorithm[M]. Beijing:Science Press, 2005. [百度学术] [Google Scholar]

段海滨 . 蚁群算法原理及其应用[M]. 北京：科学出版社, 2005. [百度学术] [Google Scholar]

Zhang Jihui，Gao Qisheng . A Self-Adaptive Ant Colony Algorithm[J]. Control Theory and Application, 2000, 17(1):1. [百度学术] [Google Scholar]

张纪会, 高齐圣 . 自适应蚁群算法[J]. 控制理论与应用, 2000, 17(1):1. [百度学术] [Google Scholar]

LI Qian,SHE Du,TANG Wei . The Application of Improved Ant Colony Algorithm in the Advance and Retreat Control of Disc Mill[J]. China Pulp & Paper,2017，36(9):48. [百度学术] [Google Scholar]

李　茜, 佘　都, 汤　伟 . 改进蚁群算法在盘磨进退刀控制中的应用[J]. 中国造纸, 2017，36(9)：48. [百度学术] [Google Scholar]

CHEN Shuqian，ZHANG Lihong . Application Reaerrch about PID Parameters Optimization Based on Ant Conlony Algotithm[J]. Computer Simulation，2011(1):238. [百度学术] [Google Scholar]

陈书谦,张丽虹 . 蚁群算法在PID控制器参数优化中的应用研究[J]. 计算机仿真,2011(1):238. [百度学术] [Google Scholar]

Tang Wei，Feng Xiaohui，Sun Zhenyu，et al . PID parameter optimization based on ant colony algorithm [J]. Journal of Shaanxi University of Science & Technology, 2017, 35(35):153. [百度学术] [Google Scholar]

汤　伟, 冯晓会, 孙振宇,等 . 基于蚁群算法的PID参数优化[J]. 陕西科技大学学报, 2017, 35(35):153. [百度学术] [Google Scholar]

Duan Haibin，Wang Daobo，Huang Xianghua，et al . Research and realization on parameters optimization of PID controller based on ant colony algorithm[J]. Engineering Journal of Wuhan University, 2004, 37(5):97. [百度学术] [Google Scholar]

段海滨, 王道波, 黄向华, 等 . 基于蚁群算法的PID参数优化[J]. 武汉大学学报(工学版), 2004, 37(5):97. [百度学术] [Google Scholar]

Wei Yanfang . Research on the Variable Domain Fuzzy PID Control of Paper Machine Synchronous Drive System[D]. Jiaozuo: He’nan Polytechnic University，2009. [百度学术] [Google Scholar]

韦延方 . 纸机同步传动系统的变论域模糊PID控制研究[D].焦作：河南理工大学,2009. [百度学术] [Google Scholar]

CPP [百度学术] [Google Scholar]

基于改进蚁群优化算法的中高速长网纸机速度链的控制

摘要

关键词

1 速度链控制原理

2 ACO的改进

2.1 ACO的基本思想

2.2 ACO数学模型

2.3 ACO的改进及仿真

3 基于改进ACO的PID参数优化

3.1 基于改进ACO的PID控制系统结构

3.2 蚁群游历节点及路径的生成[参考文献 14 Google Scholar 百度学术 14]

3.3 蚁群游历节点及路径的选择

3.4 PID参数优化整定步骤[参考文献 15 Google Scholar 百度学术 15]