网刊加载中。。。

使用Chrome浏览器效果最佳，继续浏览，你可能不会看到最佳的展示效果，

确定继续浏览么?

复制成功，请在其他浏览器进行阅读

空气过滤纸结构性能波动对过滤性能的影响

齐佩云 ¹
严春晓 ¹
金彦任 ²
赵婷 ²
臧传芹 ¹
高缨 ³
张鸿鹏 ¹
胡晓春 ¹
程振兴 ¹

1. 陆军防化学院，北京，102205； 2. 山西新华化工有限责任公司，山西太原，030008； 3. 96901部队，北京,100094

中图分类号： TS77

最近更新：2019-10-31

DOI：10.11980/j.issn.0254-508X.2019.10.009

摘要

通过测试某型号空气过滤纸的厚度、定量、紧度、阻力和过滤效率，利用统计分析软件SPSS19.0进行数据分析，考察空气过滤纸厚度、定量与紧度波动对阻力和过滤效率的影响。结果表明，空气过滤纸厚度范围在0.376~0.420 mm时，对其阻力和过滤效率测量值均不存在显著性影响（α=0.05）；定量为55.2～59.8 g/m²时，对阻力测量值有显著性影响（α=0.05），定量W与阻力Δp之间的线性回归方程为：Δp=2.641W，相关系数R² 为0.817，定量对空气过滤纸的过滤效率测量值不存在显著性影响（α=0.05）；紧度为0.139～0.152 g/m³时，对阻力和过滤效率测量值不存在显著性影响（α=0.05）。

关键词

空气过滤纸; SPSS软件; 变异; 阻力; 过滤效率

空气过滤纸是空气过滤器的关键原材料，过滤纸细而柔软的纤维错综交织构成了多孔结构，空气过滤器利用过滤纸这种结构特点滤除有毒、有害气溶胶微粒，达到净化空气的目的，其过滤效率通常为99.6%~99.999%^[

1]。空气过滤纸主要应用于现代化建筑中的空调系统以及冶金、电子、航空等生产领域洁净厂房，在军用过滤吸收器与防毒面具中也得到广泛应用，用于过滤有毒烟雾^{[参考文献 2
Google Scholar 百度学术}2,3,4]。

影响空气过滤纸过滤性能（阻力和过滤效率）的因素极其复杂，空气过滤纸的阻力计算见公式（1）。

$Δ p = A_{1} L$

（1）

式中，Δp为阻力，Pa；L为厚度，cm；A ₁为与空气过滤纸纤维结构、空气黏度及气流比速有关的常数。

当A ₁一定时，阻力随空气过滤纸厚度增加呈直线上升；当空气过滤纸厚度、空气黏度、气流比速等一定时，阻力与空气过滤纸纤维结构有关，空气过滤纸的定量和紧度是表征空气过滤纸纤维结构的两个参数，纤维密度增大时，空气过滤纸单位面积和体积内含有的纤维数量增多，当气流通过空气过滤纸时，在单位面积和体积内遇到的阻碍增多，压降损失增大，阻力增加。

空气过滤纸的过滤效率 $η$ =1‒穿透率，其穿透率计算见公式（2）。

$K = e^{- k_{1} L}$

（2）

式中，K为穿透率，%；L为厚度，cm；k ₁为与空气过滤纸纤维结构、气溶胶性质及气流速度等有关的常数。

当k ₁一定时，穿透率随厚度增加呈指数下降。当空气过滤纸厚度、气溶胶性质、气流速度等一定时，穿透率与空气过滤纸纤维结构有关，纤维越密，空气过滤纸定量和紧度越大，纤维间空隙宽度越小，扩散、惯性及截留效应越强，穿透率越小。

在造纸过程中，若纸张在干燥部的横向收缩不均一、压光机和压榨部附加压力不均匀或辊面温度不均匀等，常会影响纸张的均一性^[

5,6]，造成纸张紧度、定量和厚度的变异（即微小范围内的数值波动）。公式（1）与公式（2）表明，纸张紧度、定量与厚度均会影响阻力和过滤效率。研究紧度、定量、厚度变异对纸张过滤性能的影响，对于查明主要影响指标、控制纸张性能变异程度有着极其重要的意义。

纸张平面上定量的变异，即纸张匀度^[

7]，是考察纸张均匀程度的指标，纸张匀度对抗张强度、耐破度、撕裂度、耐折度等纸张通用性能的影响已有相关研究^{[参考文献 8
Google Scholar 百度学术}8,9]，但空气过滤纸紧度变异、匀度与厚度变异对过滤效率和阻力影响的研究鲜有报道。

假设检验是根据一定假设条件由样本推断总体的一种统计推断方法，回归分析是通过实验和观测来寻找变量之间关系的一种统计学分析方法，两者在解决实际问题中的应用十分广泛。本实验通过测量某型号空气过滤纸不同位置的厚度、定量和紧度，以及空气黏度、气溶胶性质、气流比速等使用条件一定时的阻力和过滤效率，根据数理统计中假设检验和线性回归分析的理论，结合SPSS软件对空气过滤纸的厚度、定量、紧度变异与阻力、过滤效率的关系进行分析，以期更好地控制影响过滤性能均一性的因素。

1 实验

1.1　材料及仪器

材料：空气过滤纸（天津市天伦造纸技术开发中心）。

仪器：测厚仪（上海六中量仪厂）、电子天平（北京赛多利斯仪器系统有限公司）、油雾仪（原苏联）、倾斜式微压计（上海虹口打字机生产合作社）。

1.2　测试方法

在某型号空气过滤纸上用铳子随机裁出54个d= 9 cm的圆形纸片，对每个试样测其厚度、定量、紧度、阻力和过滤效率。

（1）厚度测试

采用测厚仪测试试样厚度，测试时将重锤以低于3 mm/s的速度缓缓放下，测试压强20 kPa。每个试样测试7个点，取平均值。

（2）定量测试

用电子天平对试样称量，按国家标准计算试样定量。

（3）紧度测试

按国家标准计算试样紧度。

（4）阻力测试

采用倾斜式微压计测试试样阻力，空气黏度为17.9×10^-6Pa/s，气流比速为0.25 L/(min•cm²）。

（5）过滤效率测试

采用油雾法测试试样过滤效率，将喷雾式油雾发生器喷出的油雾通过空气过滤纸，用浊度计测定透过前和透过后的浓度，从而计算出透过系数K，过滤效率 $η$ =1-K。油料为30^#透平油，油雾浓度为42 mg/m³，油雾粒径0.28~0.34 μm，气流比速为0.25 L/(min•cm²)。

1.3　基于SPSS软件的数据统计分析方法

1.3.1　假设检验

假设两样本来自正态总体，进行均值比较时常使用t检验方法。两独立样本的t检验，用于检验2个样本是否来自具有相同均值的总体，基本步骤如下。

（1）提出零假设 $H_{0}$ ： $μ_{1} = μ_{2}$ ，和备择假设 $H_{A}$ ： $μ_{1} \neq μ_{2}$ 。

（2）计算t统计量，公式为 $t = \frac{{\bar{x}}_{1} - {\bar{x}}_{2}}{S_{{\bar{x}}_{1} - {\bar{x}}_{2}}}$ ，自由度为 $d f = (n_{1} - 1) + (n_{2} - 1)$ 。 $S_{{\bar{x}}_{1} - {\bar{x}}_{2}}$ 为两样本均值之差的标准误差，理论计算见公式（3）。

$S_{{\bar{x}}_{1} - {\bar{x}}_{2}}$ =

$\sqrt[]{\frac{\sum (x_{1} - {\bar{x}}_{1})^{2} + \sum (x_{2} - {\bar{x}}_{2})^{2}}{(n_{1} - 1) + (n_{2} - 1)} • (\frac{1}{n_{1}} + \frac{1}{n_{2}})}$

（3）

当 $n_{1} = n_{2} = n$ 时， $S_{{\bar{x}}_{1} - {\bar{x}}_{2}}$ 计算见公式（4）。

$S_{{\bar{x}}_{1} - {\bar{x}}_{2}}$ =

$\begin{array}{l} \sqrt[]{\frac{\sum (x_{1} - {\bar{x}}_{1})^{2} + \sum (x_{2} - {\bar{x}}_{2})^{2}}{n (n - 1)}} = \sqrt[]{\frac{{S_{1}}^{2}}{n} + \frac{{S_{2}}^{2}}{n}} \\ = \sqrt[]{{S_{X_{1}}}^{2} + {S_{X_{2}}}^{2}} \end{array}$

（4）

式中， $n_{1}$ 、 $n_{2}$ ； ${\bar{x}}_{1}$ 、 ${\bar{x}}_{2}$ ； ${S_{1}}^{2}$ 、 ${S_{2}}^{2}$ 分别为2个样本的样本量、样本均值、样本方差。

（3）根据 $d f = (n_{1} - 1) + (n_{2} - 1)$ ，确定临界t值t _0.05，做出统计判断。

SPSS19.0软件中，计算得到t检验统计量的观测值以及t分布的P值。当检验统计量的P值小于显著性水平时，则拒绝零假设，认为两独立样本均值有显著性差异；反之，则接受零假设，两独立样本均值无显著性差异^[

10]。

需要注意的是，t检验要求两个独立总体具有相等的方差，这是构造和选择t统计量的关键。SPSS19.0软件中利用Levene方差齐性检验方法检验两总体方差是否相等，当检验统计量的P值大于显著性水平时，则接受零假设，认为两独立样本方差相等；反之，则拒绝零假设，方差不相等。

1.3.2　一元线性回归分析

回归模型研究 $Y$ 与 $X$ 之间的关系，见公式（5）。

$E (Y) = μ (X) + ε, X = (x_{1}, x_{2}, \dots, x_{n})$

（5）

式中， $Y$ 是因变量； $X$ 是自变量； $ε$ 是随机变量（或称为随机误差），表示其他随机因素对因变量影响的总和，一般假设它是独立并服从正态分布N~(0，σ)的随机变量。

观察值 $y_{1}, y_{2}, \dots, y_{n}$ 之间的差异，由回归偏差（即变量 $x$ 引起的偏差）和残余误差（包括实验误差以及其他未控因子）两方面引起。

回归方程拟合优度检验引入相关系数R ²，其计算见公式（6）。

$R^{2} = \frac{\overset{n}{\sum_{i = 1}} (y_{i} {- \hat{y_{i}})}^{2}}{\overset{n}{\sum_{i = 1}} (y_{i} {- \bar{y})}^{2}}$

（6）

式中， $\hat{y_{i}}$ 为回归值； $y$ 为观测值； $\bar{y}$ 为观测值的算术平均值；n为观测值的数量。

相关系数R ²反映了使用Y与X之间的线性回归模型来估计 $y_{i}$ 的均值而导致总的离差平方和减少的程度，从而代表了Y与X之间的线性相关程度及回归模型的拟合优良程度。R ²越大，Y与X之间的线性相关程度越高，模型的拟合优良程度越好；R ²越小，Y与X之间的线性相关程度越低，模型的拟合优良程度越差^[

11]。

回归方程显著性检验采用F检验法，F统计量的计算见公式（7）。

$F = \frac{\overset{n}{\sum_{i = 1}} (y_{i} {- \hat{y_{i}})}^{2}}{\overset{n}{\sum_{i = 1}} {(\hat{y_{i}} - \bar{y})}^{2} / (n - 2)}$

（7）

给定显著性水平α后，可确定临界值F _α，与根据计算得到的F统计量的值进行比较。若F>F _α，表明回归效果显著；若F<F _α，表明回归效果不显著。SPSS软件中，通常直接给出拒绝零假设的概率。当P值<0.05时，接受零假设，回归效果显著；当P值>0.05时，拒绝零假设，回归效果不显著^[

12]。

需要注意的是，回归模型的建立是在残差正态性、同方差性、独立性、无偏性的假设下进行的，因此需对残差进行检验。当“P-P图”中各点分布离对角线较近时，说明残差服从均值为零的正态分布；“标准化残差散点图”中各点均匀分布时，说明残差服从方差相等的正态分布^[

13]；“Durbin-Waston统计量”接近2时，说明残差序列独立；“个案诊断”给出残差超过3倍标准差的异常值，应在回归分析中剔除该值。

2 结果与讨论

2.1　纸张各指标统计分析数据对比

对空气过滤纸54个试样各指标的测试结果如下：厚度范围为0.376~0.420 mm，定量范围为55.2~60.8 g/m²，紧度范围为0.139~0.152 g/m³，阻力范围为144~162 Pa，过滤效率范围为99.2552%~99.8828%。表1为各指标的统计分析数据。

表1 空气过滤纸各指标统计分析数据

性能参数	厚度/mm	定量/g•m^-2	紧度/g•cm^-3	阻力/Pa	过滤效率/%
平均值μ	0.397	57.8	0.146	155	99.6054
标准偏差σ	0.013	1.7	0.004	4	0.1345
变异系数V/%	3.4	2.9	2.7	2.6	0.1

各指标数据的均一性用变异系数 $V$ 表示，其计算见公式（8），变异系数越小，说明数据均一性越好。

$V = \frac{σ}{μ} \times 100$ %

（8）

由表1可知，厚度变异稍大于定量变异和紧度变异，但均符合过滤纸厚度、定量偏差不超过5%^[

14]的一般生产要求，空气过滤纸的两大性能指标阻力和过滤效率具有一定的变异性，过滤效率变异相对于阻力变异更小，说明过滤效率测试值的均一性较好，初步推测厚度、定量、紧度的变异引起过滤效率测量值变异的可能性较小。

2.2　厚度和定量变异对空气过滤纸过滤性能的影响

基于SPSS软件的假设检验和回归分析方法，讨论空气过滤纸厚度、定量、紧度变异是否造成阻力和过滤效率测量值的显著性差异。

2.2.1　厚度变异对阻力的影响

在表1的54个样本中，筛选定量范围缩小至（57.8±1.4）g/m²（相应的紧度范围为0.139~0.152 g/m³）的24个样本，将相应样本的厚度分为0.376~0.395 mm和0.396~0.420 mm两组，每组样本12个。利用SPSS软件对所得阻力数据进行独立样本均值t检验，检验结果如表2所示。

表2 两组不同厚度变异空气过滤纸的阻力SPSS软件独立样本检验

	方差方程的Levene检验		均值方程的 t 检验
	F	P值	t	df	P值 (双侧)	均值差值	标准误差值	差分的 95% 置信区间
	F	P值	t	df	P值 (双侧)	均值差值	标准误差值	下限	上限
方差相等	3.140	0.090	-1.210	22	0.239	-1.583	1.308	-4.296	1.130
方差不等			-1.210	15.057	0.245	-1.583	1.308	-4.371	1.204

由表2可知，F=3.140，P值=0.090>0.05，说明两组数据方差相等，t检验结果的双侧P值0.239>0.05，即在0.05的显著性水平时，厚度在0.376~0.420 mm范围内波动，对空气过滤纸的阻力测试值没有显著性影响。

由于厚度、定量和紧度与阻力之间的关系都是正相关，排除三者对阻力的影响相互抵消的可能，说明厚度在0.376~0.420 mm范围内波动，不影响空气过滤纸的阻力测试值。需要说明的是，这批纸张原定量、紧度波动范围大，若按此批数据处理，发现两组厚度变异不同的空气过滤纸阻力值不一致，究其原因可能是厚度变异单独影响或是定量变异单独影响，或是两者综合影响（即紧度的影响）所致。因此，进一步筛选定量波动范围窄的纸张厚度、定量和紧度数据进行处理，发现厚度不同时阻力数据一致。所以，定量缩到更小范围内是厚度变异不影响阻力测试值结论的前提条件。

2.2.2　定量变异对阻力的影响

在表1的54个样本中，筛选空气过滤纸厚度缩小至（0.397±0.010）mm的24个样本，将相应样本的定量分为55.2~57.4 g/m²和57.5~59.8 g/m²两组，每组样本12个。利用SPSS软件对所得阻力数据进行独立样本均值t检验，检验结果如表3所示。

表3 两组不同定量变异空气过滤纸的阻力SPSS软件独立样本检验

	方差方程的 Levene 检验		均值方程的 t 检验
	F	P值	t	df	P值 (双侧)	均值差值	标准误差值	差分的 95% 置信区间
	F	P值	t	df	P值 (双侧)	均值差值	标准误差值	下限	上限
方差相等	1.899	0.182	-5.713	22	0.000	-6.427	1.125	-8.759	-4.094
方差不等			-5.558	17.849	0.000	-6.427	1.156	-8.858	-3.996

由表3可知，F=1.899，P值=0.182>0.05，说明两组数据方差相等，t检验结果的双侧P值0.000<0.05，即在0.05的显著性水平时，定量在55.2~59.8 g/m²范围内波动，对阻力测试值有显著性影响。

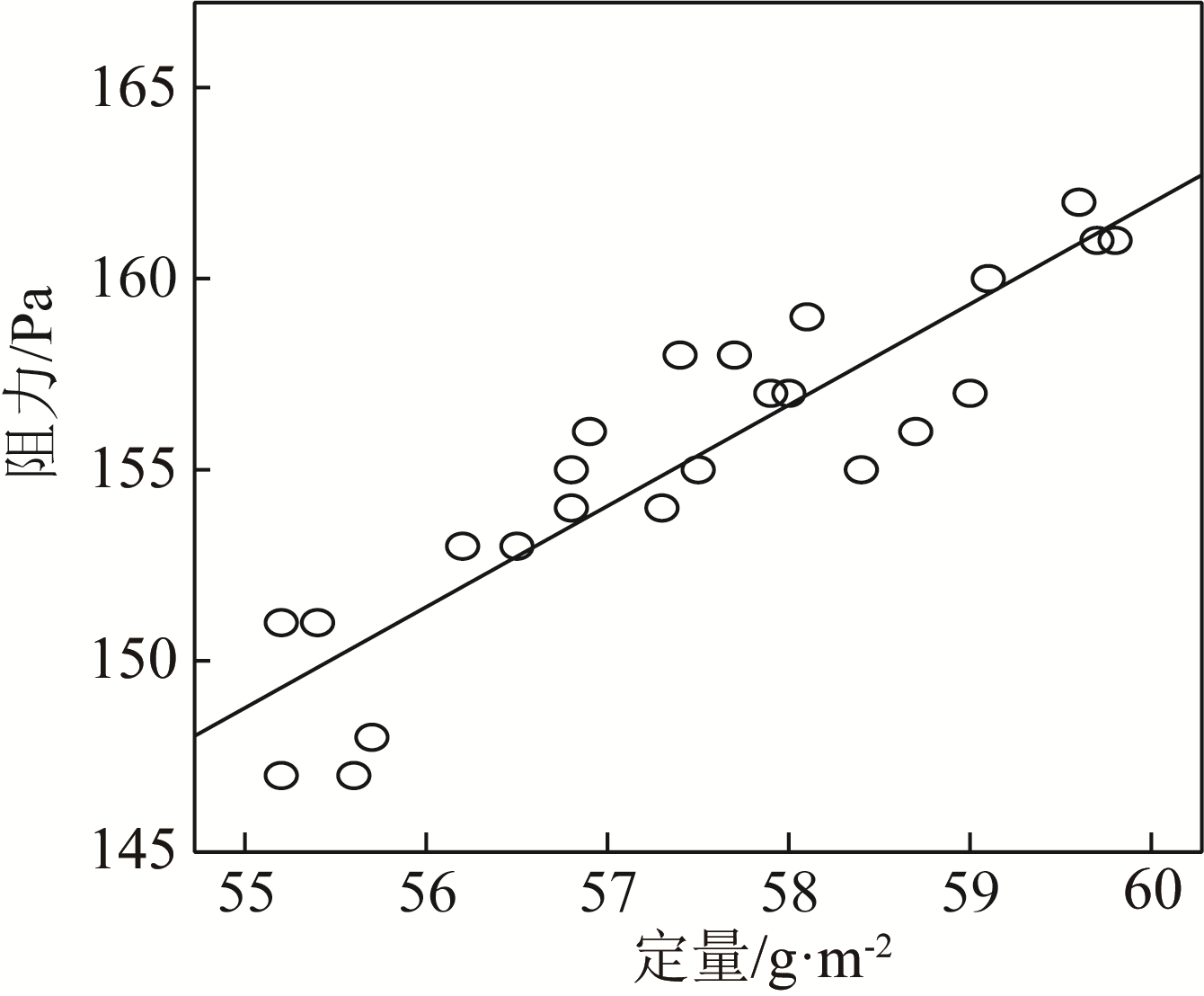
采用SPSS软件简单线性回归模型，分析定量波动对空气过滤纸阻力测试值的影响，如图1所示。通过绘制散点图，直接判断两者之间存在线性关系，建立线性回归方程并对其进行检验。图2为正态P-P图，图2中各点分布接近对角线，说明残差接近于正态分布（简单线性回归仅要求回归残差接近于正态分布）；图3为标准化残差散点图，由图3可以看出，观察点随机地散布在横轴的周围，说明残差存在等方差性；Durbin-Watson统计量（见表6）为1.438，在2附近，说明残差独立，无异常值。

图1 阻力与滤纸定量的散点图

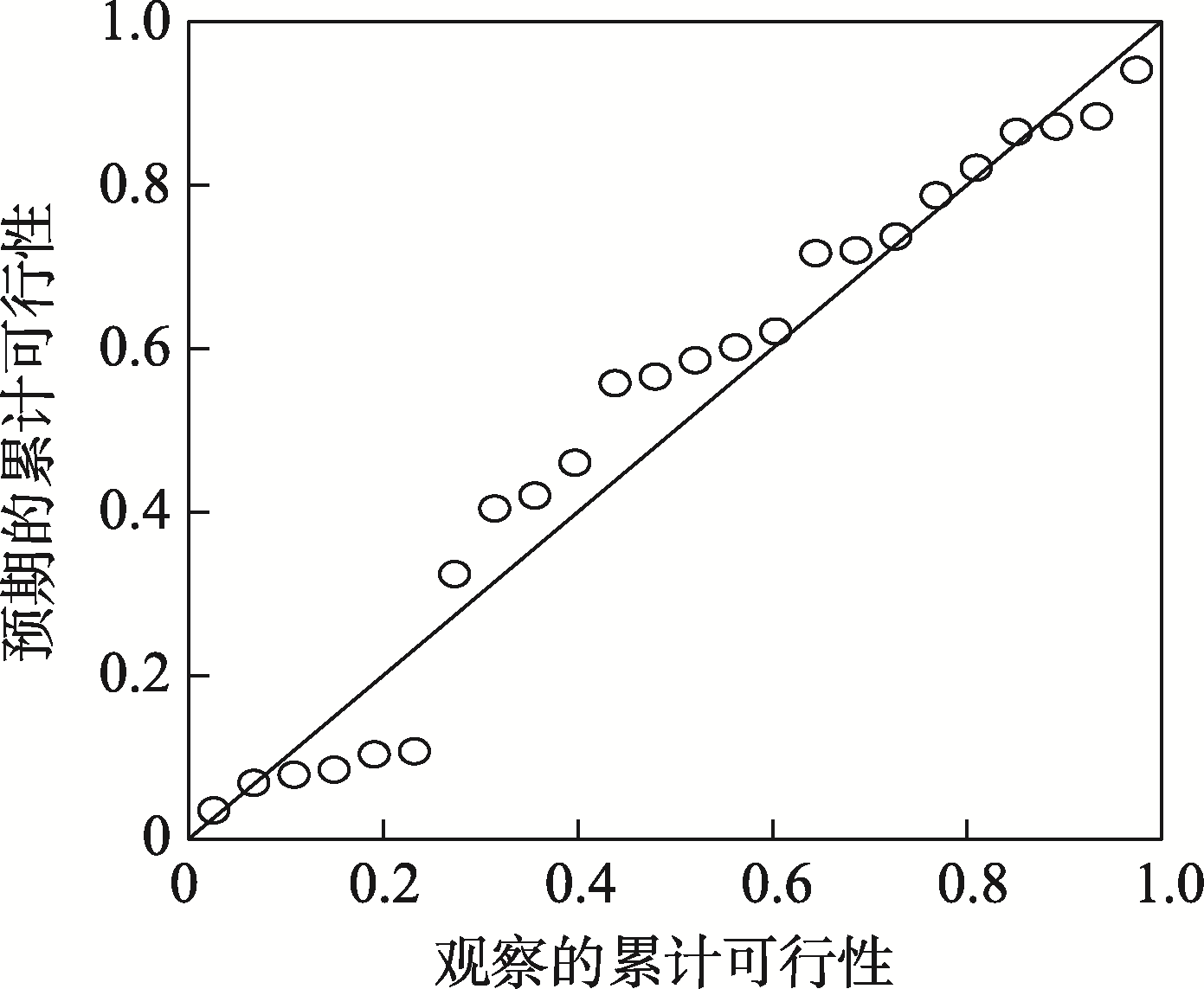
图2 正态P-P图

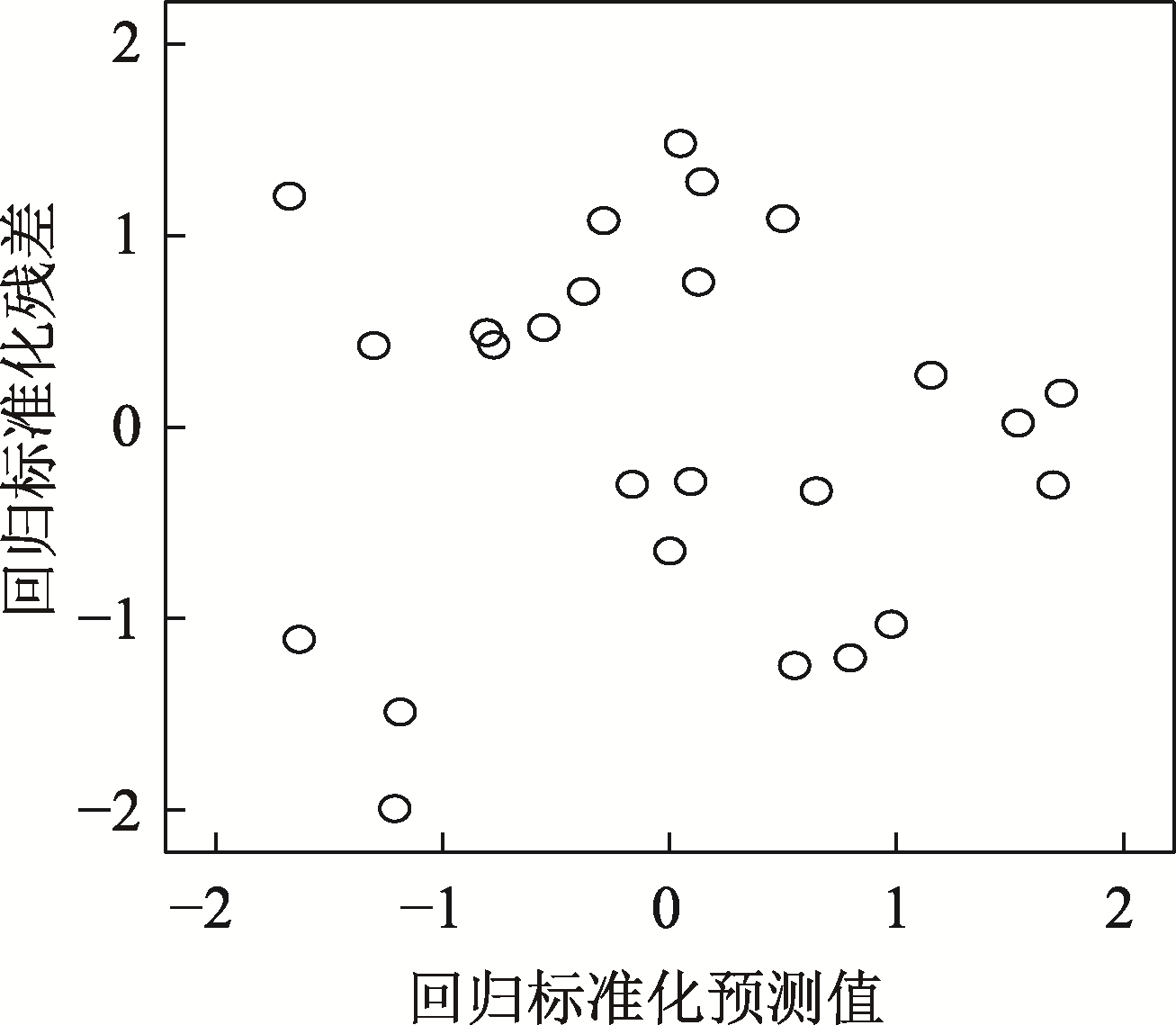
图3 标准化残差散点图

表6 模型汇总

R	R ²	调整 R ²	标准估计的误差	Durbin-Watson
0.904	0.817	0.809	1.851	1.438

表4是通过SPSS软件得到的空气过滤纸阻力与定量回归模型的回归系数（截距和斜率）。标准化系数β是指将数据标准化后分析得出的系数，用来反映被解释变量的重要性；非标准化系数 B 是指用实验原始数据分析得出的系数，用来做实际的预测。本实验主要做实际的预测，因此采用非标准化系数。由表4可知，斜率、截距非标准化系数分别为2.641、3.491，P值分别为0.000、0.822。按α=0.05显著性水平，分析认为空气过滤纸的定量与阻力之间存在较为显著的线性关系，但截距不能通过显著性检验，不应纳入方程。因此建立的多元回归方程见公式（9）。

表4 空气过滤纸阻力与定量回归模型的回归系数

模型	非标准化系数	标准化系数	t	P值
截距斜率	3.491	15.316		0.228	0.822
2.641	0.267	0.904	9.909	0.000

模型

非标准化系数

标准化系数

P值

标准误差

截距

斜率

3.491

15.316

0.228

0.822

2.641

0.267

0.904

9.909

0.000

Δp=2.641W （9）

式中，Δp为阻力，Pa；W为定量，g/m²。

表5为回归方程的显著性检验结果，采用的是F检验（即方差齐性检验）。由表5可知，F(1,22)=98.188，P值=0.000<0.05，表明所得的回归方程在α<0.05的水平时显著，即空气过滤纸的定量变异对阻力的影响有统计学意义。

表5 回归方程的显著性检验结果

模型	平方和	df	均方	F	P值
回归残差	336.551	1	336.551	98.188	0.000
75.408	22	3.428
总计	411.958	23

模型

平方和

均方

P值

回归

残差

336.551

98.188

0.000

75.408

3.428

总计

411.958

表6是模型汇总表，给出了反映该模型拟合优良程度的相关系数R ²，由表6可知，R ²=0.817，说明阻力变化的81.7%是由纸张的定量偏差引起的，影响程度较高。

2.2.3　紧度变异对阻力的影响

在表1的54个样本中，筛选空气过滤纸厚度缩小至（0.397±0.010）mm的24个样本，将相应样本的紧度分为0.139~0.145 g/m³和0.146~0.152 g/m³两组，每组样本12个。利用SPSS软件对所得阻力数据进行独立样本均值t检验，检验结果如表7所示。

表7 两组不同紧度变异空气过滤纸的阻力SPSS软件独立样本检验

	方差方程的 Levene 检验		均值方程的 t 检验
	F	P值	t	df	P值 (双侧)	均值差值	标准误差值	差分的95%置信区间
	F	P值	t	df	P值 (双侧)	均值差值	标准误差值	下限	上限
方差相等	0.021	0.885	0.544	22	0.592	0.958	1.761	⁃2.694	4.610
方差不等			0.544	21.367	0.592	0.958	1.761	⁃2.699	4.615

由表7可知，F=0.021，P值=0.885>0.05，说明两组数据方差相等，t检验结果的双侧P值0.592>0.05，即在0.05的显著性水平时，紧度在0.139~0.152 g/m³范围内波动，对空气过滤纸的阻力测试值没有显著性影响。

2.2.4　厚度变异对过滤效率的影响

按厚度将表1的54个样本分为0.376~0.395 mm和0.396~0.420 mm两组，每组样本27个。利用SPSS软件对所得过滤效率测量值进行独立样本均值t检验，检验结果如表8所示。

表8 两组不同厚度变异空气过滤纸的过滤效率SPSS软件独立样本检验

	方差方程的 Levene 检验		均值方程的 t 检验
	F	P值	t	df	P值 (双侧)	均值差值	标准误差值	差分的 95% 置信区间
	F	P值	t	df	P值 (双侧)	均值差值	标准误差值	下限	上限
方差相等	0.190	0.665	0.074	52	0.942	0.0027	0.0370	-0.0714	0.0769
方差不等			0.074	51.089	0.942	0.0027	0.0370	-0.0714	0.0769

由表8可知，F=0.190，P值=0.665>0.05，说明两组数据方差相等，t检验结果的双侧P值0.942>0.05，即在0.05的显著性水平时，厚度在0.376~0.420 mm范围内波动，对空气过滤纸的过滤效率测试值没有显著性影响。

2.2.5　定量变异对过滤效率的影响

将表1的54个样本按定量分为55.2~57.4 g/m²和57.5~60.8 g/m²两组，每组样本27个。利用SPSS软件对所得过滤效率测量值进行独立样本均值t检验，检验结果如表9所示。

表9 两组不同定量变异空气过滤纸的过滤效率SPSS软件独立样本检验

	方差方程的 Levene 检验		均值方程的 t 检验
	F	P值	t	df	P值 (双侧)	均值差值	标准误差值	差分的95%置信区间
	F	P值	t	df	P值 (双侧)	均值差值	标准误差值	下限	上限
方差相等	0.345	0.559	-0.561	52	0.577	-0.0207	0.0368	-0.0946	0.0533
方差不等			-0.561	51.689	0.577	-0.0207	0.0368	-0.0946	0.0533

由表9可知，F=0.345，P值=0.559>0.05，说明两组数据方差相等，t检验结果的双侧P值0.577>0.05，即在0.05的显著性水平时，定量在55.2~60.8 g/m²范围内波动，对空气过滤纸的过滤效率测试值没有显著性影响。

2.2.6　紧度变异对过滤效率的影响

将表1的54个样本按紧度分为0.139~0.145 g/m³和0.146~0.152 g/m³两组，每组样本27个。利用SPSS软件对所得过滤效率测量值进行独立样本均值t检验，检验结果如表10所示。

表10 两组不同紧度变异空气过滤纸的过滤效率SPSS软件独立样本检验

	方差方程的 Levene 检验		均值方程的 t 检验
	F	P值	t	df	P值 (双侧)	均值差值	标准误差值	差分的95%置信区间
	F	P值	t	df	P值 (双侧)	均值差值	标准误差值	下限	上限
方差相等	3.918	0.053	-0.664	52	0.510	-0.0244	0.0368	-0.0983	0.0494
方差不等			-0.664	46.561	0.510	-0.0244	0.0368	-0.0985	0.0496

由表10可知，F=3.918，P值=0.053>0.05，说明两组数据方差相等，t检验结果的双侧P值0.510>0.05，即在0.05的显著性水平时，紧度在0.139~0.152 g/m³范围内波动，对空气过滤纸的过滤效率测试值没有显著性影响。

3 结论

本课题以空气过滤纸为测试样品，测得其厚度范围为0.376~0.420 mm，定量范围为55.2~60.8 g/m²，紧度范围为0.139~0.152 g/m³，阻力范围为144~162 Pa，过滤效率范围为99.2552%~99.8828%，并采用SPSS统计分析软件分别研究了厚度、定量和紧度波动对阻力、过滤效率测试值的影响。

3.1　厚度范围缩小至（0.397±0.010）mm时，空气过滤纸的定量范围为55.2~59.8 g/m²，紧度范围为0.139~0.152 g/m³，此时定量会引起阻力值的变化，其关系式为Δp=2.641W，相关系数R ²为0.817；紧度不会引起阻力变化。定量范围缩小至（57.8±1.4） g/m²时（相应的紧度范围为0.139~0.152 g/m³），厚度对阻力测试值没有显著性影响。

3.2　空气过滤纸的过滤效率变异小，α=0.05时，空气过滤纸的厚度、定量、紧度波动对其过滤效率测试值均没有显著性影响。

参考文献

ZHANG Gui⁃ping . Air Filter Paper and Its Research Direction[J]. Tianjin Paper Making, 1994（2）: 4. [百度学术] [Google Scholar]

张桂萍 . 空气过滤纸及其研究方向[J]. 天津造纸, 1994（2）: 4. [百度学术] [Google Scholar]

XIANG Hai⁃qing, NI Xiao⁃ping, GAO Yan, et al . Examination of Air Purifying Efficiency of Negative-Pressure Cover of Mobile Bed Unit[J]. Chinese Journal of Disinfection, 2005, 22(2): 153. [百度学术] [Google Scholar]

项海青, 倪晓平, 高炎, 等 . 移动式床单位负压罩空气净化效果的检测[J]. 中国消毒学杂志, 2005, 22(2): 153. [百度学术] [Google Scholar]

SUN Meng⁃nan, DI Jun⁃ping, ZHOU Zi⁃jing, et al . The Mechanism of Oil Mist Separation and the Filtration Performance of Glass Fiber Filter Paper[J]. Journal of Filtration & Separation, 2007, 27(3): 24. [百度学术] [Google Scholar]

孙梦楠, 狄俊平, 周子敬, 等 . 油雾分离机理及玻纤滤纸过滤性能的研究[J]. 过滤与分离, 2007, 27(3): 24. [百度学术] [Google Scholar]

KANG Dingxue . ULPA Filter Paper[J]. China Pulp & Paper, 1997, 3(2): 15. [百度学术] [Google Scholar]

康定学 . 超细微粒空气过滤纸[J]. 中国造纸, 1997, 3(2): 15. [百度学术] [Google Scholar]

ZHANG Sufeng, ZHANG Meiyun, HE Fan, et al . Relation between Components of Sheet Formation and Aramid Paper Properties[J]. China Pulp & Paper, 2008, 27(7): 25. [百度学术] [Google Scholar]

张素风, 张美云, 何方, 等 . 芳纶纸匀度分量和定量对性能的影响[J]. 中国造纸, 2008, 27(7): 25. [百度学术] [Google Scholar]

WANG Hui, WU Shao⁃ping, WANG Yong-wei, et al . The Influence of the Forming Section Control on Art Paper Formation on Gap Former[J]. China Pulp & Paper, 2014, 33(1): 37. [百度学术] [Google Scholar]

王晖, 巫劭平, 王永伟, 等 . 夹网纸机网部控制对铜版原纸匀度的影响[J]. 中国造纸, 2014, 33(1): 37. [百度学术] [Google Scholar]

YANG Bo⁃jun . Evenness of paper sheet[J]. China Pulp & Paper Industry, 2004, 25(3): 32. [百度学术] [Google Scholar]

杨伯钧 . 纸的匀度[J]. 中华纸业, 2004, 25(3): 32. [百度学术] [Google Scholar]

Fan Huiming, Wang Ming . Study on the Relationship between the Formation Index and the Air Permeability of Paper[J]. Paper Science & Technology, 2013, 32(6): 116. [百度学术] [Google Scholar]

樊慧明, 王命 . 纸张匀度指数与透气度关系的研究[J]. 造纸科学技术, 2013, 32(6): 116. [百度学术] [Google Scholar]

Wang Qiuyun, Dong Rongye . Approaches to Improve Paper Formation[J]. Papermaking Chemicals, 2005(4): 40. [百度学术] [Google Scholar]

王秋云, 董荣业 . 纸张匀度的改进措施[J]. 造纸化学品, 2005(4): 40. [百度学术] [Google Scholar]

MU Ling⁃ling, YIN Zhi⁃jun, YANG Zhan⁃chang . On the Evaluation Method of Technology Economics Based on T-test and Hierarchical Clustering[J]. Journal of Hebei Software Institute, 2012, 14(1): 24. [百度学术] [Google Scholar]

牟玲玲, 尹志军, 杨占昌 . 基于t检验和聚类分析的技术经济学成绩综合评价研究[J]. 河北软件职业技术学院学报, 2012, 14(1): 24 [百度学术] [Google Scholar]

Wei Xinxing, Lu Yugui . Several Statistical Software Implementation of the Linear Regression Analysis[J]. Journal of Hechi University, 2017, 37(5): 64. [百度学术] [Google Scholar]

韦新星, 卢玉桂 . 线性回归分析的几种统计软件实现[J]. 河池学院学报, 2017, 37(5): 64. [百度学术] [Google Scholar]

Gong Yanping, Wang Jie . Application of Single Regression Analysis on Wastewater Treatment Plant[J]. Environmental Protection Science, 2013, 39(2): 13. [百度学术] [Google Scholar]

宫艳萍, 王劫 . 一元回归分析在污水处理厂中的应用[J]. 环境保护科学, 2013, 39(2):13. [百度学术] [Google Scholar]

Liu Qing⁃qing . A Linear Regression Analysis in Insurance Industry[J]. Journal of Dezhou University, 2012, 28(6): 23. [百度学术] [Google Scholar]

刘情情 . 一元线性回归分析在保险行业的应用[J]. 德州学院学报, 2012, 28(6): 23. [百度学术] [Google Scholar]

HAN Hongsheng . Quality Control of Base Papers for Coated Grades[J]. China Pulp & Paper, 2008,27(8): 48. [百度学术] [Google Scholar]

韩红生 . 涂布原纸的质量控制[J]. 中国造纸, 2008,27 (8): 48. [百度学术] [Google Scholar]

CPP [百度学术] [Google Scholar]

空气过滤纸结构性能波动对过滤性能的影响

摘要

关键词

1 实 验

1.1 材料及仪器

1.2 测试方法

（1）厚度测试

（2）定量测试

（3）紧度测试

（4）阻力测试

（5）过滤效率测试

1.3 基于SPSS软件的数据统计分析方法

1.3.1 假设检验

1.3.2 一元线性回归分析

2 结果与讨论

2.1 纸张各指标统计分析数据对比

2.2 厚度和定量变异对空气过滤纸过滤性能的影响

2.2.1 厚度变异对阻力的影响

2.2.2 定量变异对阻力的影响

2.2.3 紧度变异对阻力的影响

2.2.4 厚度变异对过滤效率的影响

2.2.5 定量变异对过滤效率的影响

2.2.6 紧度变异对过滤效率的影响

3 结 论