网刊加载中。。。

使用Chrome浏览器效果最佳，继续浏览，你可能不会看到最佳的展示效果，

确定继续浏览么?

复制成功，请在其他浏览器进行阅读

预测造纸废水出水指标的随机森林建模方法

辛辰 ¹
刘鸿斌 ^1,2

1. 南京林业大学林业资源高效加工利用协同创新中心，江苏南京，210037； 2. 华南理工大学制浆造纸工程国家重点实验室，广东广州，510640

中图分类号： X793； TP27

发布日期：2019-08-20

DOI：10.11980/j.issn.0254-508X.2019.08.010

摘要

出水化学需氧量（COD）与出水固形物含量（SS）是评价造纸废水处理工艺好坏的重要指标。为了更好地对其进行预测，提出了一种基于随机森林（RF）模型的方法，并以R语言为工具进行回归预测。对比偏最小二乘（PLS）模型、支持向量回归（SVR）模型、人工神经网络（ANN）模型等常规预测模型，发现RF模型具有预测精度高，结果误差小，泛化能力好，调整参数少等优点。在对出水COD进行预测时，RF模型的相关系数r为0.7954，相比于PLS、SVR、ANN分别提高了8.88%、10.73%、14.68%。在对出水SS进行预测时，RF模型的相关系数r为0.8551，相比于PLS、SVR、ANN分别提高了15.43%、24.25%、30.79%。

关键词

废水处理过程; 随机森林模型; 出水指标; 回归模型

在造纸废水处理工艺中，往往需要根据出水指标来及时调整工艺条件，达到对污水的安全排放。然而考虑到造纸废水处理过程中大多包含具有时变性与复杂性的化学过程，传统化学成分检测仪表存在价格高昂、维护成本高以及检测不灵敏等缺点。近年来，基于数据驱动的软测量建模方法可通过建立输入与输出数据的关系来完成易测变量对难测变量的预测^[

1]，也可以对造纸废水处理过程中出现的故障进行检测^{[参考文献 2
查找原文}2]，因而得到广泛的应用。

常见的软测量建模方法有人工神经网络（Artificial Neural Networks, ANN）、支持向量回归（Support Vector Regression, SVR）、偏最小二乘法（Partial Least Squares, PLS）^[

3]。PLS具有克服变量相关性和噪声干扰等优点，因此PLS在工业生产过程中应用较广，但该方法属于线性方法，对于具备典型非线性特征的造纸废水处理过程，其预测精度明显下降。基于此，杨浩等人^{[参考文献 4
查找原文}4]在PLS的基础上研究改进得到了递归偏最小二乘法（RPLS），有效地提高了模型的预测精度。ANN模型的工作方式类似于人脑神经元处理信息的方式^{[参考文献 5
查找原文}5]，Zeng等人^{[参考文献 6
查找原文}6]提出将ANN预测模型应用于造纸废水处理过程。李晓东等人^{[参考文献 7
查找原文}7]利用ANN模型对城市废水排放量进行了预测研究。虽然ANN对于预测过程中的非线性特征具备较强的解释能力，但该方法也存在一定的缺点。如为了得到最好的网络结构，需要通过大量的排列组合去寻优；网络权值在线调整比较困难，可能出现训练过早结束，权值衰退现象^{[参考文献 8
查找原文}8]；此外，模型的过拟合问题也难以避免^{[参考文献 9
查找原文}9]。相比ANN模型，SVR模型在输入数据中有选择的寻找有限向量，比ANN对全体样本迭代计算速度快^{[参考文献 10
查找原文}10]。汪瑶等人^{[参考文献 11
查找原文}11]通过粒子群优化算法对SVR模型进行参数优化，优化后的模型相比ANN模型预测精度显著提高。张世峰等人^{[参考文献 12
查找原文}12]以溶解氧为控制对象，提出一种支持向量机（SVM）与PID结合的复合控制系统。支持向量机模型除了可以用于预测真实数据外，还可以在已知故障分类下预测数据的故障类型^{[参考文献 13
查找原文}13]。但当样本离散程度较高且样本数过少时，模型难以有效还原总体的全部信息，预测精度不高^{[参考文献 14
查找原文}14]。

随机森林（Random Forest，RF）模型是由Leo Breiman与Adele Cutler在2001年提出的一种统计学习模型^[

15]，是一种结合Bagging和随机选择特征的高效新型的组合方法，广泛用于样本数据的分类和回归预测。相比于上述机器学习模型，RF模型泛化能力更强，在不结合其他优化方法的前提下仍有较高的预测精度，且建模过程中需要调整的参数较少。RF模型在金融学、生物学、医学、电力通信领域中有着广泛的应用^{[参考文献 16
查找原文}16,17,18]，但在废水出水指标预测方面并未得到应用。因此，本课题应用RF模型对出水化学需氧量（COD）与出水固形物含量（SS）进行预测并分析预测效果，同时对比了ANN、SVR、PLS方法的预测效果。

1 RF模型建模原理和评价指标

1.1　建模原理

RF模型由K棵决策树 ${h = (X, θ_{K}), K = 1, 2, \dots, k}$ 组成，其中 ${θ_{K}, K = 1,2, \dots, k}$ 是一个随机变量序列。当模型用于分类时，RF模型中的决策树使用分类树（一般使用C4.5），最终通过少数服从多数的原则决定分类结果，当模型用于回归预测时，决策树使用回归树（一般用CART），最终将所有决策树输出值的平均值作为预测结果^[

15]。RF模型最大的优势便是其多样性，依照集成学理论来说，基学习器的多样性越强，其泛化能力就越好。RF模型的随机思想主要体现在以下两方面。

（1）Bagging思想^[

15]

在原始训练集中，利用Bootstrap抽样方法有放回地抽取若干个大小相同的数据集样本。原始训练集中每个样本未被抽到的概率为(1–1/N) ^N ，所以当N足够大时，(1–1/N) ^N 将收敛于1/e≈0.368。这部分占比接近37%的数据即为袋外数据，使用这些袋外数据可以对已有模型进行检验。于是，每棵决策树对应一个误差率，即OOB(out-of-bag)误差率，根据误差率可进一步优化模型。

（2）随机特征思想^[

19]

为保证RF模型的随机性最大化，每棵树在节点分裂的过程中，都会从所有特征中选出最优特征作为参考指标。对于RF模型而言，如果选择过少的特征，则会导致模型的精度降低。如果选择的特征过多，则会弱化模型在分裂节点处的随机性^[

20]。本课题采用基尼指数（Gini）^{[参考文献 21
查找原文}21]作为选择依据选出最佳特征数。

1.2　RF模型的建模步骤

（1）在原始训练集S中，通过Bootstrap重抽样的方法取出n个数据集样本，然后将每个数据集样本分为抽中样本即袋内数据（in-bag）和未被抽中样本即袋外数据（out-of-bag）。

（2）从样本的所有属性中随机抽取m个属性，根据Gini指标进行节点分裂，用袋内数据训练构建CART树。在构建的过程中不进行修剪，使得每一棵CART树充分地生长。

（3）用未参与建模的袋外数据去检验对应的CART树，通过袋外数据的预测误差确定最佳决策树数量。

（4）利用建好的模型去预测测试集中的新数据，将所有CART树的预测结果平均值作为最终的预测结果。

RF模型建模流程图如图1所示。

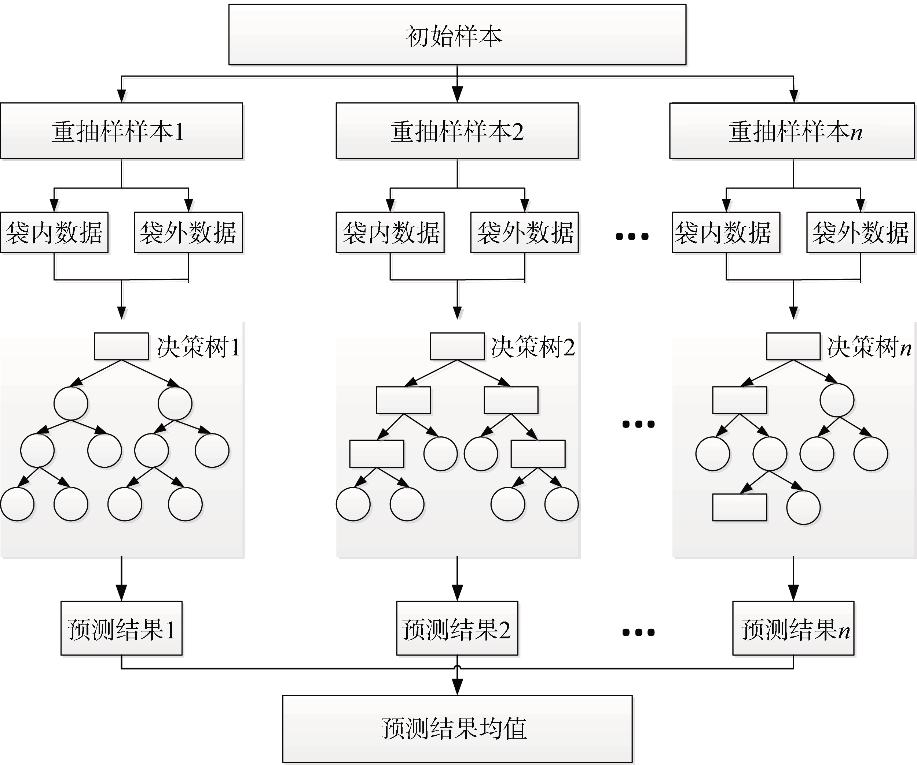
图1 随机森林建模流程

1.3　预测模型的性能评价指标

实验引入相关系数（r）、平均绝对百分比误差（MAPE）与均方根误差（RMSE）作为模型评价指标，通过对比其他预测模型，发现RF模型在预测性能方面有明显优势。其中r越大，MAPE与RMSE越小，表明模型的预测效果越好，对应的计算公式如公式(1)所示。

$r = \frac{\overset{N}{\sum_{t = 1, i = 1}} (y_{t} - {\bar{y}}_{t}) ({\hat{y}}_{i} - {\bar{y}}_{i})}{\sqrt[]{\overset{N}{\sum_{t = 1}} (y_{t} - {\bar{y}}_{t})^{2} . \overset{N}{\sum_{i = 1}} ({\hat{y}}_{i} - {\bar{y}}_{i})^{2}}}$

$M A P E = \frac{1}{N} \overset{N}{\sum_{i = 1}} |\frac{y_{t} - {\hat{y}}_{i}}{y_{t}}| \times 100$

$R M S E = \sqrt[]{\frac{\overset{N}{\sum_{t = 1, i = 1}} ({\hat{y}}_{i} - y_{t})^{2}}{N}}$

（1）

式中，y_t 为测量值， ${\hat{y}}_{i}$ 为模型预测值， ${\bar{y}}_{t} = \overset{N}{\sum_{t = 1}} y_{t}$ ， ${\bar{y}}_{i} = \overset{N}{\sum_{i = 1}} y_{i}$ ， ${\bar{y}}_{t}$ 、 ${\bar{y}}_{i}$ 分别为y_t 与 ${\hat{y}}_{i}$ 的平均值。

2 实验过程与结果

2.1　造纸废水数据分析

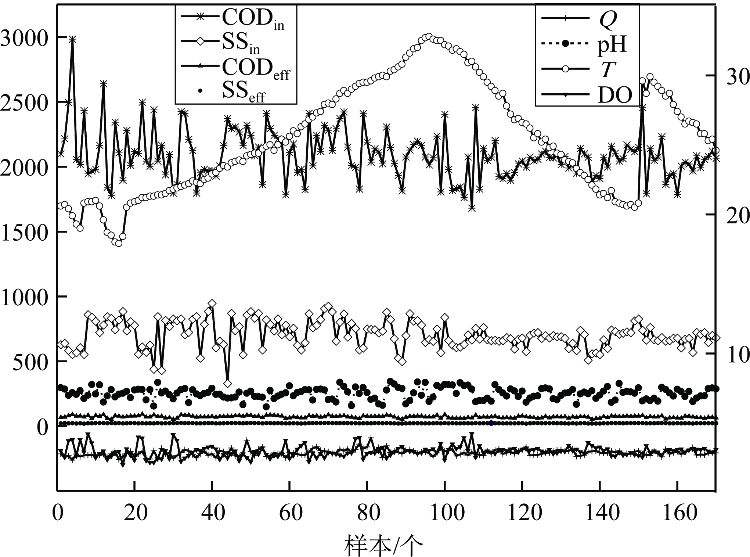
实验通过利用如图2所示的某造纸废水处理厂的170组样本数据进行研究，每组数据包括8个变量，分别为：废水总流量Q、进水悬浮固形物含量SS_in、温度T、进水化学需氧量COD_in、pH值、溶解氧含量DO、出水化学需氧量COD_eff、出水悬浮固形物含量SS_eff。将COD_eff、SS_eff作为预测模型的输出变量，Q、SS_in、COD_in、pH值、T、DO作为输入变量。按照时间先后的顺序，将前120组数据作为训练集样本，后50组数据作为测试样本，建立RF回归模型，确立预测变量与其影响变量之间的非线性关系。

图2 造纸废水处理过程数据

注：

图中左边纵坐标表示COD_in（mg/L）、SS_in（mg/L）、COD_eff（mg/L）和SS_eff（mg/L）；右边纵坐标表示Q（10⁴ m³/d）、pH值、T（℃）和DO（mg/L）。

2.2　RF模型及其对比模型的建立

2.2.1　RF模型的建立

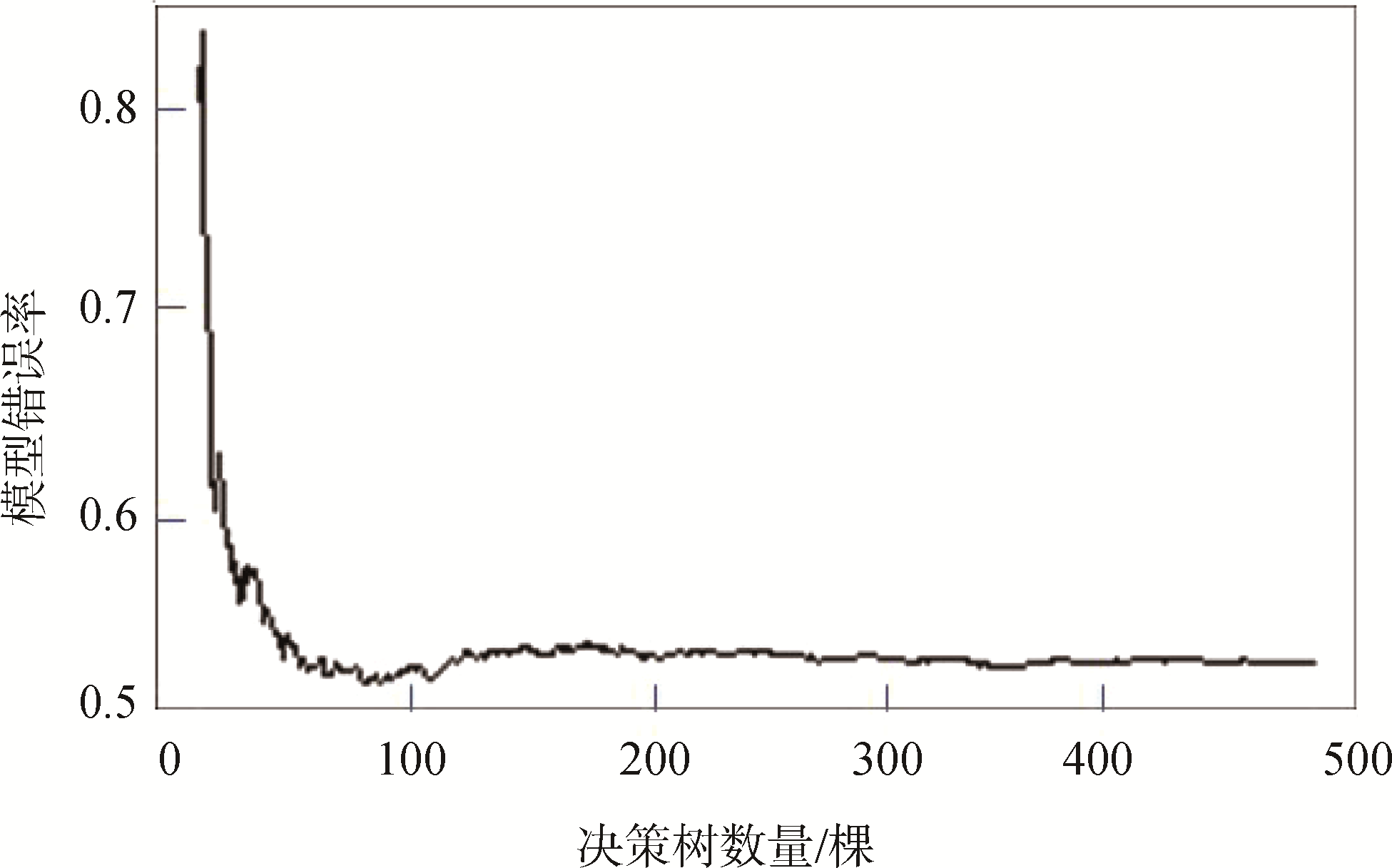
建模的主要函数为R语言中randomForest包中的randomForest函数。该函数中需要寻优的主要参数有2个，分别为决策树的棵数n_tree与树节点的变量个数m_try，其默认参数分别为n_tree=500，m_try=M/3（M为变量总个数）。参数的可调范围分别为n_tree∈[1,500]，m_try∈[1,M]。考虑到较少的决策树使得模型效果无法完全发挥，模型错误率偏高，而较多的决策树则会提升模型复杂程度，使得模型训练与预测速度下降，并有可能出现轻微的过拟合现象。本课题通过调用R语言自带函数plot对模型错误率与决策树数量的关系可视化处理如图3所示。由图3可知，RF模型中树的棵数n_tree取200时，OOB（out-of-bag）误差波动已经趋于稳定，即实验可以选用n_tree=200。选出最优决策树棵数后继续做了补充验证实验，即不断增加决策树的棵数到500棵并观察模型预测效果。结果表明，模型预测效果变化不明显甚至有轻微下降的趋势，证明了决策树最优棵数为200。树节点预选的变量数m_try根据基尼指数选取最优值，基尼指数越大表明样本属于某类的不确定性就越大。因为本次实验数据的变量个数较少，所以依次计算了不同变量数对应的基尼指数，基尼指数最小时对应的节点变量数为m_try=4。为了进一步验证所选的节点变量数为最优变量数，后续补充实验分别用m_try=1、m_try=2、m_try=3、m_try=5、m_try=6进行建模,观察模型最后的预测效果即相关系数（r）、平均绝对百分比误差（MAPE）与均方根误差（RMSE）等指标，结果同样表明当m_try=4时，预测效果最好。

图3 模型错误率与决策树数量关系图

2.2.2　对比模型的建立

建立3种对比模型前先需要将数据标准化处理，之后用前120组数据进行建模，后50组数据用来检验预测效果。SVR模型所利用的主要程序包为R语言中的rminer包，其中模型参数选用SVM。ANN模型建模所利用的程序包主要为AMORE包。通过大量的实验选出构建模型的最佳参数为：模型的网络总层数为3层，包含1个输入层、1个隐含层和1个输出层，其中输入层节点数为6，隐含层节点数为2，输出层节点数为1，隐含层采用tansig激活函数，输出层采用purelin激活函数。根据赤池信息量准则，PLS模型最终选择了3个与预测变量相关度最大的自变量作为输入变量，分别为COD_in、SS_in、DO。

2.3　结果与讨论

经过模型的建立及后续的优化后，表1列出了RF模型与其他3种模型的预测结果。对测试集COD_eff的预测效果进行比较，相关性方面，RF模型对应的r为0.7954，ANN、SVR、PLS，对应的r分别为0.6936、0.7183、0.7305；误差方面，RF模型对应的RMSE与MAPE最小，分别为4.2471和5.2606，相比于ANN、SVR、PLS，其RMSE与MAPE分别降低了19.18%和7.55%、19.20%和15.75%、12.06%和7.67%。对测试集SS_eff的预测效果进行比较，相关性方面，RF模型对应的r为0.8551, ANN、SVR、PLS对应的r分别为0.6538、0.6882、0.7408；误差方面，RF模型对应的RMSE与MAPE最小，分别为0.6687和2.0633，相比于ANN、SVR、PLS，其RMSE与MAPE分别降低了20.69%和26.21%、17.03%和29.83%、17.35%和28.60%。

表1 不同模型对COD_eff和出水SS_eff的预测结果

模型		COD_eff			SS_eff
模型		RMSE	MAPE/%	r	RMSE	MAPE/%	r
ANN	训练集	4.4769	4.3996	0.8528	0.6942	2.3299	0.8084
ANN	测试集	5.2566	6.5094	0.6936	0.8431	2.7962	0.6538
SVR	训练集	4.3545	4.3149	0.8521	0.5726	2.1600	0.8757
SVR	测试集	5.0413	5.6905	0.7183	0.8123	2.9403	0.6882
PLS	训练集	4.7541	5.2146	0.8264	0.7897	2.8166	0.7555
PLS	测试集	4.8293	5.6979	0.7305	0.8091	2.8899	0.7408
RF	训练集	2.3473	2.4533	0.9656	0.3745	1.3577	0.9648
RF	测试集	4.2471	5.2606	0.7954	0.6687	2.0633	0.8551

总体而言，RF模型在预测精准度方面都优于其他3种常用的回归预测模型，图4为RF模型对COD_eff和SS_eff的预测效果图。

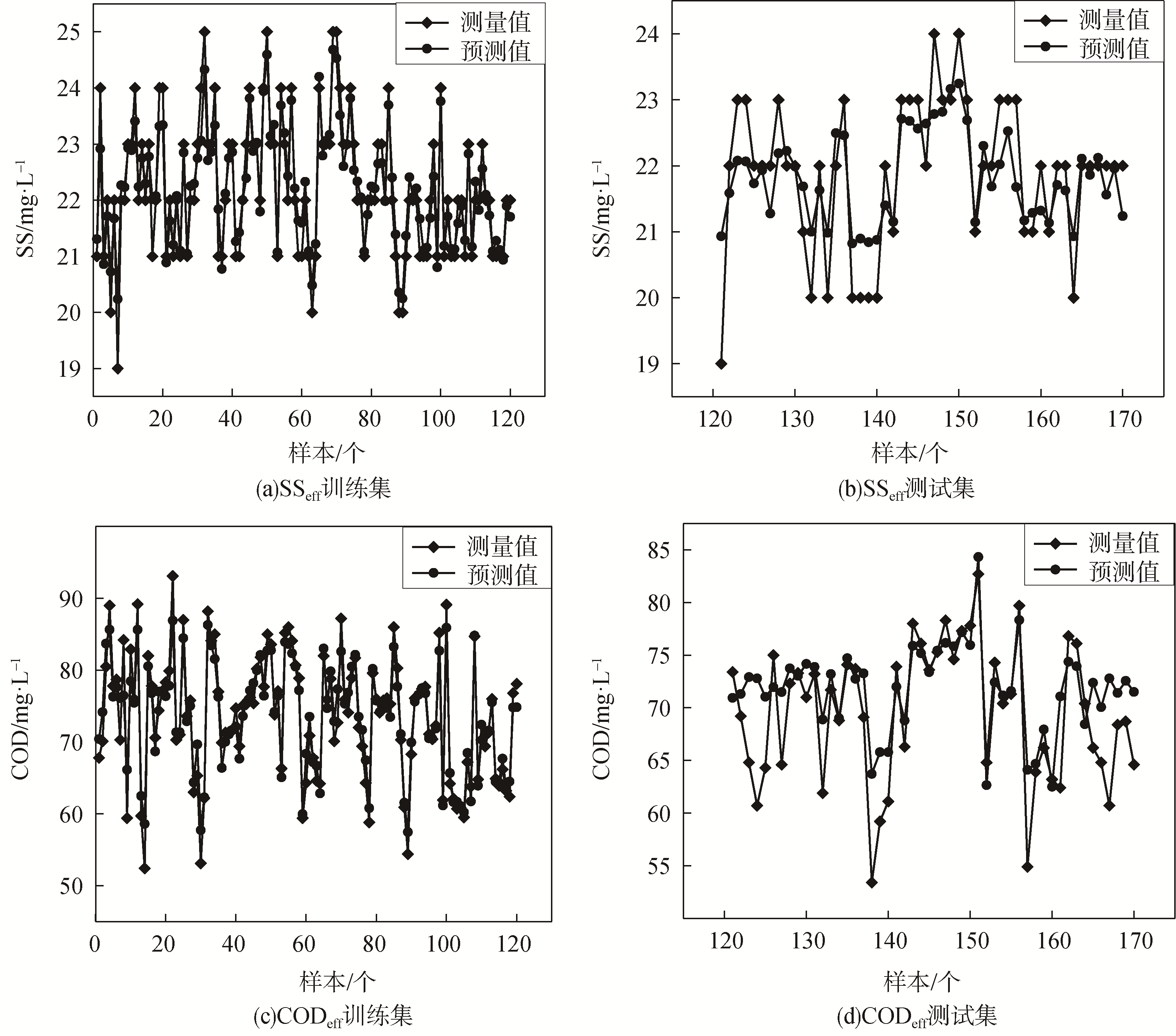
图4 RF模型对SS_eff和COD_eff的预测结果

RF模型比其他3种模型预测效果好的主要原因在于RF模型的泛化能力更强，实验中所用到的RF模型包含200棵决策树，而每棵决策树的生长只利用了训练集中的一部分样本，同时只抽取样本属性中的部分属性。采用该方法极大地提高了决策树的多样性，弱化了各棵决策树的相关性。同时，RF模型需要调整的主要参数只有2个，即决策树的棵数与树节点预选的变量个数，且易于寻找最优参数。

相比之下，虽然ANN模型具有较强的非线性拟合能力，但在构建模型的过程中，所要考虑的参数种类过多，在初始值、动量因子、网络结构、节点个数等参数方面没有统一规范的寻优方法，尝试通过原理推导或实验结果比较进行寻找最优参数是一件耗时费力的工作，往往会出现训练集预测效果较好，但测试集预测效果时好时坏的情况，容易出现过拟合现象，模型的泛化能力一般。SVR虽然相比于ANN过拟合现象得到了弱化，但根据实验预测效果来看并不是很理想，想要进一步提升预测效果还需要在原始模型上增添优化函数。PLS模型预测效果虽然比ANN模型与SVR模型好，但其线性模型的本质限制了它进一步优化的空间，且实验结果证明PLS模型只适合选择3个自变量作为输入变量，并不能充分地利用收集到的数据所蕴含的信息。

ANN、SVR、PLS在进行预测前，也都需要对数据进行标准化处理，实验中统一用z-score方法标准化，目的就是为了在建模过程中让不同的自变量具有相同的尺度，对因变量的影响程度基本相同。RF模型与上述3种方法相比省去了这一步骤，因为每棵决策树的生成过程都是依次用到部分自变量，所以不同尺度的自变量之间互不影响。

3 结论

本课题分别采用随机森林（RF）模型、偏最小二乘（PLS）模型、支持向量回归（SVR）模型与人工神经网络（ANN）模型对造纸废水中的COD_eff与SS_eff指标进行了回归预测。

3.1 通过与其他3种模型的预测结果比较得出：基于随机森林回归模型的预测效果最好，预测值与真实值之间不仅相关性更高，且误差更小，泛化能力更强。

3.2 随机森林回归模型相比其他3种模型，数据无需标准化处理，寻找最优参数时所要调整的参数较少且容易寻优，易于进一步的推广。

参考文献

Zhu Xue-feng，Li Yan，Huang Dao-ping . The Overview on Control and Optimization in Wastewater Treatment Processes[J]. Automation & Information Engineering，2009, 30(3): 7.

朱学峰，李艳，黄道平 . 污水处理过程的控制与优化综述[J]. 自动化与信息工程, 2009, 30(3): 7.

WANG Lingsong，MA Pufan，YE Fengying，et al . Incipient Fault Detection in Papermaking Wastewater Treatment Processes[J]. China Pulp & Paper，2017, 36(8): 20.

王龄松，马璞璠，叶凤英，等 . 造纸废水处理过程微小故障检测方法研究[J]. 中国造纸, 2017, 36(8): 20.

Cao Peng-fei，Luo Xiong-lin . Modeling of Soft Sensor for Chemical Process[J]. CIESC Jorunal，2013, 64(3): 788.

曹鹏飞，罗雄麟 . 化工过程软测量建模方法研究进展[J]. 化工学报, 2013, 64(3): 788.

YANG Hao，MO Weilin，XIONG Zhixin，et al . Soft Sensor Modeling of Papermaking Effluent Treatment Processes Using RPLS[J]. China Pulp & Paper，2016, 35(10): 31.

杨浩，莫卫林，熊智新，等 . 基于RPLS的造纸废水处理过程软测量建模[J]. 中国造纸, 2016, 35(10): 31.

Li Di，Tang Hui，Wan Jin-quan，et al . ANN-based Dynamic Modeling of Wastewater Treatment Process in Paper Making by Waste Paper[J]. Journal of South China University of Technology(Natural Science Edition)，2005, 33(12): 42.

李迪，唐辉，万金泉，等 . 基于ANN的废纸造纸废水处理过程的动态建模[J]. 华南理工大学学报（自然科学版）, 2005, 33(12): 42.

Zeng G M，Qin X S，He L，et al . A Neural Network Predictive Control System for Paper Mill Wastewater Treatment[J]. Engineering Applications of Artificial Intelligence, 2003, 16(2): 121.

Li Xiao-dong，Zeng Guang-ming，Huang Guo-he，et al . Chaos Neural Network (NN) Model for Short Term Predicting on the Influent Time Series of WWTP[J]. Acta Scientiae Circumstantiate，2006, 26(3): 416.

李晓东，曾光明，黄国和，等 . 城市污水量短时预测的混沌神经网络模型[J]. 环境科学学报, 2006, 26(3): 416.

Feng Rui，Zhang Hao-ran，Shao Hui-he . Soft Sensor Modeling Based on Support Vector Machine[J]. Information and Control，2002, 31(6): 567.

冯瑞，张浩然，邵惠鹤 . 基于SVM的软测量建模[J]. 信息与控制, 2002, 31(6): 567.

Zhou Zhi-hua，Chen Shi-fu . Neural Network Ensemble[J]. Chinese Journal of Computers，2002, 25(1): 1.

周志华，陈世福 . 神经网络集成[J]. 计算机学报, 2002, 25(1): 1.

LIU Hongbin，LI Xiangyu，YANG Chong . Soft Sensor Modeling of Papermaking Waste Water Treatment Process Using PCA Dimensional Reduction Models[J]. Transactions of China Pulp and Paper，2018, 33(4): 50.

刘鸿斌，李祥宇，杨冲 . 基于PCA降维模型的造纸废水处理过程软测量建模[J]. 中国造纸学报, 2018, 33(4): 50.

WANG Yao，XU Liang，YIN Wenzhi，et al . Soft Sensor Modeling of Papermaking Wastewater Treatment Processes Based on ANN and LSSVR[J]. Transactions of China Pulp and Paper，2017, 32(1): 50.

汪瑶，徐亮，殷文志，等 . 基于ANN和LSSVR的造纸废水处理过程软测量建模[J]. 中国造纸学报, 2017, 32(1): 50.

Zhang Shi-feng，Yang Cheng，Li Xiao-ming . Research on Sewage Treatment Based on LS_SVM[J]. Industrial Control Computer，2013, 26(4): 66.

张世峰，杨成，李晓明 . 基于LSSVM逆系统在污水处理系统DO控制中的研究[J]. 工业控制计算机, 2013, 26(4): 66.

Li Xiangyu，Yang Chong，Song Liu，et al . Fault Diagnosis of Papermaking Wastewater Treatment Processes Based on Support Vector Machine[J]. Transactions of China Pulp and Paper，2018, 33(3): 55.

李祥宇，杨冲，宋留，等 . 基于支持向量机的造纸废水处理过程故障诊断[J]. 中国造纸学报, 2018, 33(3): 55.

Yang Da-lian，Liu Yi-lun，Zhou Wei，et al . Fatigue Life Prediction of Large-Span Samples Based on the Optimized SVR Model[J]. Journal of Northeastern University (Natural Science Edition)，2015 (9): 1321.

杨大炼，刘义伦，周维，等 . 基于优化 SVR 模型的大跨度样本疲劳寿命预测[J]. 东北大学学报（自然科学版）, 2015(9): 1321.

Breiman L . Bagging predictors[J]. Machine Learning, 1996, 24(2): 123.

Cao Wen-zhe，Ying Jun，Chen Guang-fei，et al . Risk Prediction and Comparitive Research of Type 2 Diabetes Mellitus Complicated with Retinopathy based on Logistic Regression and Random Forest Algorithm[J]. China Medical Equipment，2016, 31(3): 33.

曹文哲，应俊，陈广飞，等 . 基于Logistic回归和随机森林算法的2型糖尿病并发视网膜病变风险预测及对比研究[J]. 中国医疗设备, 2016, 31(3): 33.

Fang Kuang-nan，Wu Jian-bin，Zhu Jian-ping，et al . A Review of Technologies on Random Forests[J]. Statistics & Information Forum，2011, 26(3): 32.

方匡南，吴见彬，朱建平，等 . 随机森林方法研究综述[J]. 统计与信息论坛, 2011, 26(3): 32.

Wu Xiao-yu，He Jing-han，Zhang Pei，et al . Power System Short-term Load Forecasting Based on Improved Random Forest with Grey Relation Projection[J]. Automation of Electric Power Systems，2015, 39(12): 50.

吴潇雨，和敬涵，张沛，等 . 基于灰色投影改进随机森林算法的电力系统短期负荷预测[J]. 电力系统自动化, 2015, 39(12): 50.

Dietterich T G . An Experimental Comparison of Three Methods for Constructing Ensembles of Decision Trees: Bagging, Boosting, and Randomization[J]. Machine Learning, 2000, 40(2): 139.

Liu Min，Lang Rong-ling，Cao Yong-bin . Number of trees in random forest[J]. Computer Engineering and Applications，2015(5): 126.

刘敏，郎荣玲，曹永斌 . 随机森林中树的数量[J]. 计算机工程与应用, 2015(5): 126.

Chen Yun-ying，Wu Ji-qin，Xu Ke-jia . Using Gini-Index for Attribute Selection in Decision Trees[J]. Microcomputer Development，2004, 14(5): 66.

陈云樱，吴积钦，徐可佳 . 决策树中基于基尼指数的属性分裂方法[J]. 微机发展, 2004, 14(5): 66.

CPP

预测造纸废水出水指标的随机森林建模方法

摘要

关键词

1 RF模型建模原理和评价指标

1.1 建模原理

1.2 RF模型的建模步骤

1.3 预测模型的性能评价指标

2 实验过程与结果

2.1 造纸废水数据分析

2.2 RF模型及其对比模型的建立

2.2.1 RF模型的建立

2.2.2 对比模型的建立

2.3 结果与讨论

3 结 论